Skip to main content

General Physics I:

Sunil Karna

Section 4.6 Examples C

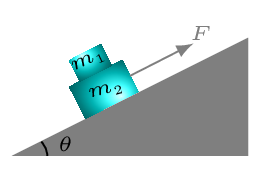
Example 4.6.1.

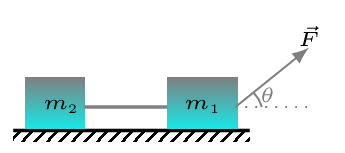
A 10-kg block lying on the horizontal surface is pulled by a force F making an angle of \(60^{o}\) above the horizontal. The coefficient of static friction between the block and the horizontal surface is 0.3 and the coefficient of kinetic friction is 0.2. Draw the appropriate diagrams, write the appropriate equations, and find the magnitude and direction of the acceleration of the block when
  1. \(\displaystyle F = 30 \,N,\)
  2. \(\displaystyle F = 60 \,N,\)
  3. \(\displaystyle F = 90 \,N,\)
  4. \(\displaystyle F = 120 \,N.\)
Solution.
Given: \(m = 10 \,kg, \quad \theta = 60^{o}, \quad \mu_{s} = 0.3, \quad \mu_{k} = 0.2, \quad g = 9.8 \,m/s^{2}.\)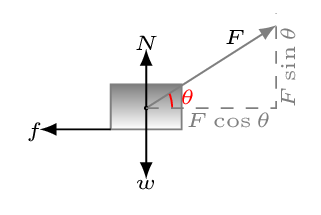
Equations:
\begin{equation*} \sum F_{x} = F \cos\theta - f = m a_{x} \end{equation*}
\begin{equation*} \sum F_{y} = F \sin\theta - w + N = m a_{y} \end{equation*}
\begin{equation*} f = \mu N; \end{equation*}
\begin{equation*} w = m g \quad \rightarrow \quad w = 98\, N \end{equation*}
  1. \(F = 30 \,N.\) In verticle direction, \(a_{y} = 0,\)
    \begin{equation*} \therefore \quad N + F \sin\theta -w = 72.02 \,N \end{equation*}
    In horizontal direction, assume \(a_x=0\) then,
    \begin{equation*} f= F\cos\theta = 30\times \cos(60) =15\,N. \end{equation*}
    and
    \begin{equation*} f_s=\mu_s N = 0.3\times 72.02 = 21.61\, N \end{equation*}
    Since \(f \lt f_{s},\) static friction can keep the block at rest as assumed. Therefore, \(a = 0, \quad \theta_{a} = 0.\)
  2. \(F = 60 \,N.\) Assume
    \begin{equation*} a_{y} = 0, \longrightarrow N = w - F \sin\theta = 46.04 \,N \end{equation*}
    and
    \begin{equation*} a_{x} = 0,\longrightarrow f = F \cos\theta = 30 \,N, \quad f_{s} = \mu_{s} N = 13.812 \,N \end{equation*}
    Since \(f \gt f_{s},\) static friction cannot keep the block at rest as assumed. Therefore block slides and,
    \begin{equation*} \mu =\mu_{k} = 0.2;\quad f = \mu N = 9.208 \,N \end{equation*}
    \begin{equation*} a_{x} = (F \cos\theta - f)/m = 2.079 \,m/s^{2} \end{equation*}
    \begin{equation*} \therefore a = 2.08 \,m/s^{2}, \quad \theta_{a} = 0. \end{equation*}
  3. \(F = 90 N.\) Assume
    \begin{equation*} a_{y} = 0, \rightarrow N = w - F \sin\theta = 20.058 \,N \end{equation*}
    Assume block slides,
    \begin{equation*} \mu = \mu_{s} = 0.2;\quad f = \mu N = 4.099 \, N \end{equation*}
    \begin{equation*} a_{x} = (F \cos\theta - f)/m = 4.011 \,m/s^{2}\qquad \therefore a = 4.01 \,m/s^{2},\quad \theta_{a} = 0. \end{equation*}
  4. \(F = 120 \,N.\) Assume
    \begin{equation*} a_{y} = 0, \rightarrow N = w - F \sin\theta = - 5.923 \,N \end{equation*}
    Since N cannot be negative, our assumption was false and block leaves the surface.
    \begin{equation*} \therefore, N = 0, \quad f = 0;\quad a_{x} = (F \cos\theta)/m = 6.000 \,m/s^{2} \end{equation*}
    \begin{equation*} a_{y} = (F \sin\theta - w)/m = 0.5923 \,m/s^{2} ; a = = 6.029 \,m/s^{2} \end{equation*}
    \begin{equation*} \tan\theta_{a} = \frac{a_{y}}{a_{x}} \rightarrow \theta_{a} = 5.638^{o} \end{equation*}
    \begin{equation*} \therefore, a = 6.03 \,m/s^{2}, \quad \theta_{a} = 5.64^{o}. \end{equation*}

Example 4.6.2.

A block of mass \(m_{1} = 10 \,kg \) rests on top of a larger block of mass \(m_{2}\) = 25 kg which rests on a plane inclined at an angle \(\theta = 10^{o}\text{.}\) The coefficient of static friction between all surfaces is \(0.3\) and that of kinetic friction is \(0.2\text{.}\) A constant force \(F\) parallel to the plane is applied to \(m_{2}\) accelerating it up the plane.
  1. What is the maximum acceleration of \(m_{2}\) which will allow \(m_{1}\) to stay with it?
  2. What is the force \(F\) which causes this acceleration?
Solution.
Given: \(m_{1} =10 \,kg, \quad m_{2} =25 \,kg,\quad \theta=10^{o}, \quad \mu_{1}=0.3,\quad \mu_{2}=0.2, \quad g =9.8 \,m/s^{2}.\)
From figure,
we have -
\begin{equation} \sum F_{x}=f_{1}-w_{1}\sin\theta=m_{1}a \tag{4.6.1} \end{equation}
\begin{equation*} \sum F_{y}=N_{1}-w_{1}\cos\theta=0 \end{equation*}
\begin{equation} \text{or,}\quad N_{1}=w_{1}\cos\theta = m_{1}g\cos\theta =10\times 9.8\times\cos 10^{o} =96.5 \,N \tag{4.6.2} \end{equation}
also,
\begin{equation} f_{1}=\mu_{1}N_{1}=0.3\times 96.5 = 28.95 \,N\tag{4.6.3} \end{equation}
now from eqn.(4.6.1),
\begin{equation} a =\frac{f_{1}-w_{1}\sin\theta}{m_{1}} = \frac{28.95-10\times9.8\times\sin 10^{o}}{10}= 1.193 m/s^{2} \tag{4.6.4} \end{equation}
From figure,
we have -
\begin{equation} \sum F_{x}=F-f_{1}-f_{2}-w_{2}\sin\theta=m_{2}a \tag{4.6.5} \end{equation}
\begin{equation*} \sum F_{y}=N_{2}-N_{1}-w_{2}\cos\theta=0 \end{equation*}
\begin{equation*} \text{or,}\quad N_{2}=N_{1}+w_{2}\cos\theta \end{equation*}
\begin{equation} =96.5+25\times9.8\times\cos 10^{o}=337.79\,N\tag{4.6.6} \end{equation}
\begin{equation} \text{also,}\quad f_{2}=\mu_{2}N_{2}=0.2\times 337.79 = 67.56 \,N\tag{4.6.7} \end{equation}
\begin{equation*} \therefore\quad F = f_{1}+f_{2}+w_{2}\sin\theta+m_{2}a \end{equation*}
\begin{equation*} = 28.95+67.56+25\times 9.8\times\sin 10^{o}+25\times1.193 = 168.88 \,N \end{equation*}

Example 4.6.3.

A box of mass 100 kg is placed in the front end of the bed of a truck initially at rest. The coefficient of static friction between box and truck bed is 0.4, the coefficient of kinetic friction between box and truck bed is 0.25, the bed of the truck is 2 m long and 1 m above the ground, and the truck accelerates at a constant acceleration just fast enough to make the box start sliding.
  1. What is the acceleration of the truck?
  2. What is the acceleration of the box?
  3. When does the box fall off the back of the truck?
  4. How far does the truck travel before the box falls off?
  5. How fast is the box traveling when it falls off the truck?
  6. How far from its starting point does the box hit the ground?
Solution.
Given: \(m = 100 kg, \quad \mu_{s} = 0.4, \quad \mu_{k} = 0.25, \) \(L = 2 \,m, \quad y = 1 \,m\)
  1. \begin{equation*} \sum F_{x} = f = m a_{2};\quad \sum F_{y} = N - w = 0 \end{equation*}
    \begin{equation*} \mu=0.4, \quad w = m g =980\,N,\quad \therefore N = 980 \,N \end{equation*}
    \begin{equation*} f = \mu N; \quad f = 392 \,N, \quad \mu = \mu_{s}, \quad \therefore\qquad a_{2} = 3.92 \,m/s^{2} \end{equation*}
  2. \begin{equation*} \mu = \mu_{k} = 0.25; \quad f = 245 \,N;\quad a_{1} = 2.45 \,m/s^{2} \end{equation*}
  3. \begin{equation*} x_{1} = v_{o1} t + \frac{1}{2}a_{1} t^{2}; \quad v_{o1} = 0; \quad L = x_{1} - x_{2} = + t^{2} \end{equation*}
    \begin{equation*} x_{2} = v_{o2} t + \frac{1}{2}a_{2} t^{2};\quad v_{o2} = 0; \quad t = = 1.65 s; \qquad x_{1} = x_{2} + L \end{equation*}
  4. \begin{equation*} x_{1} = \frac{1}{2}a_{1} t^{2} = 5.33 \,m \end{equation*}
  5. \begin{equation*} v_{2} = v_{o2} + a_{2} t; v_{2} = 4.04 \,m/s \end{equation*}
  6. \begin{equation*} x_{3} = v_{2} t_{2}; t_{2} = 0.452 \,s \end{equation*}
    \begin{equation*} y = \frac{1}{2}g t_{2}^{2}; x_{3} = 1.825\, m \end{equation*}
    \begin{equation*} x_{T} = x_{1} + x_{3}; \quad x_{T} = 7.16 \,m \end{equation*}

Example 4.6.4.

Pulley A is fixed to the ceiling, pulley B is suspended by the string whose one end is attached to the ceiling and another end is passing over pulley B and holding the block 1 of mass \(m_{1}\) as shown in figure below. The block 2 of mass \(m_{2}\) is hanging from the pulley B. If the pulleys and strings are massless and the strings do not stretch. What is the correct relationship between accelerations \(a_{1}\) and \(a_{2}\) of blocks 1 and 2?
Solution.
Since the pulleys are massless, tensions of each section of the string in either side of pulleys are same as shown in figure.
To find the relation between \(a_{1}\) and \(a_{2}\) add the lengths of each section of the string and take its derivative as shown below. Let \(H\) is the height of pulley A from reference level (ground level), then length of string from pulley A to block 1 is given as \(H-y_{1},\) length of section of string from pulley A to B is \(H-y_{2}\) and length of section of string from pulley B to level of pulley A is \(H-y_{2}\text{.}\)
Ignore the lengths of string over pulleys and to the rest to ceiling. It does not contribute any thing to the derivative of the length. Now
\begin{equation*} L=(H-y_{1})+(H-y_{2})+(H-y_{2}) = 3H -y_{1}-2y_{2} \end{equation*}
where \(y_{a}\) and \(y_{2}\) are distances of block 1 and pulley B from the reference level, respectively. Since the string does not stretch, we have -
\begin{equation*} \frac{\,dL}{\,dt} = 0 = 0 -\frac{\,dy_{1}}{\,dt} -2\frac{\,dy_{2}}{\,dt} \end{equation*}
\begin{equation*} \therefore \frac{\,dy_{1}}{\,dt} = -2\frac{\,dy_{2}}{\,dt} \quad \Rightarrow\quad v_{1}=-2v_{2} \end{equation*}
That is velocity of block 1 \(v_{1} \) is just the double velocity of block 2 \(v_{2}\) and negative sign indicates the velocity of block 2 is opposite to that of block 1. Again,
\begin{equation*} \frac{\,dv_{1}}{\,dt} = -2\frac{\,dv_{2}}{\,dt} \end{equation*}
\begin{equation} \therefore a_{1}=-2a_{2} \tag{4.6.8} \end{equation}
From free-body diagram, we have -
\begin{equation} m_{1}g-T=m_{1}a_{1} \qquad \therefore\quad T=m_{1}g-m_{1}a_{1} \tag{4.6.9} \end{equation}
\begin{equation} \text{also}\quad T_{2}-m_{2} g = m_{2}a_{2} \qquad \therefore\quad T_{2}=m_{2}g+m_{2}a_{2} \tag{4.6.10} \end{equation}
\begin{equation} \text{but}\quad T_{2} = T +T \qquad \therefore \quad 2T = m_{2}g+m_{2}a_{2} \tag{4.6.11} \end{equation}
\begin{equation*} 2\left[m_{1}g-m_{1}a_{1}\right] = m_{2}g+m_{2}a_{2} \end{equation*}
\begin{equation*} \text{or,}\quad 2 m_{1}g -m_{2}g = m_{2}a_{2}+2m_{1}a_{1} \end{equation*}
\begin{equation*} \text{or,}\quad \left(2 m_{1} -m_{2}\right) g = -m_{2}\frac{a_{1}}{2}+2m_{1}a_{1} = a_{1}\left(2m_{1}-\frac{m_{2}}{2}\right) \end{equation*}
\begin{equation*} \therefore \quad a_{1} = \left[\frac{\left(2 m_{1} -m_{2}\right) g}{\left(2m_{1}-\frac{m_{2}}{2}\right)}\right] \end{equation*}
\begin{equation*} \text{and}\quad T = \frac{m_{1}m_{2}g}{4m_{1}-m_{2}} \end{equation*}

Example 4.6.5.

A 30 N force is applied at an angle of \(37^{o} \) to the horizontal to move the two boxes attached to each other with a string. If the force is applied on the box of mass 3kg and the mass of second box is 1 kg, find the acceleration of the boxes and tension in the string. Consider the kinetic friction between the surfaces of box and the road is 0.4.
Solution.
Given: \(\mu_{k}=0.4, \quad m_{1}=3 \,kg, \quad m_{2}=1 \,kg, \quad F=30\,N, \quad \theta=37^{o},\) and \(g=9.8\, m/s^{2}. \)
From free body diagram,
we have -
\begin{equation} \sum F_{x}=T-f_{2} =m_{2}a \qquad \Rightarrow\quad T=m_{2}a+f_{2}\tag{4.6.12} \end{equation}
\begin{equation} \sum F_{y}=N_{2}-m_{2}g =0 \qquad \Rightarrow\quad N_{2}=m_{2}g \tag{4.6.13} \end{equation}
\begin{equation} \text{but,}\quad f_{2}=\mu_{k}N_{2}\tag{4.6.14} \end{equation}
\begin{equation} \therefore\quad T = m_{2}(a+\mu_{k}g) \tag{4.6.15} \end{equation}
From free body diagram,
we have -
\begin{equation} \sum F_{x}=F_{x}-T-f_{1} = m_{1}a \qquad \Rightarrow\quad T=F_{x} - m_{1}a-f_{1}\tag{4.6.16} \end{equation}
\begin{equation} \sum F_{y}=N_{1}+F_{y}-m_{1}g =0 \qquad \Rightarrow\quad N_{1}=m_{1}g -F_{y} \tag{4.6.17} \end{equation}
\begin{equation} \text{but,}\quad f_{1}=\mu_{k}N_{1}\tag{4.6.18} \end{equation}
\begin{equation} \therefore\quad T = F\left(\cos\theta +\mu_{k}\sin\theta\right) -m_{1}(a+\mu_{k}g) \tag{4.6.19} \end{equation}
On solving eqns. (4.6.15) and (4.6.19), we have - \(a=3.0 \,m/s^{2}\) and \(T=6.92 \,N.\)
PrevTopNext