Subsection 7.1.9 Moment of Inertia of a Sphere
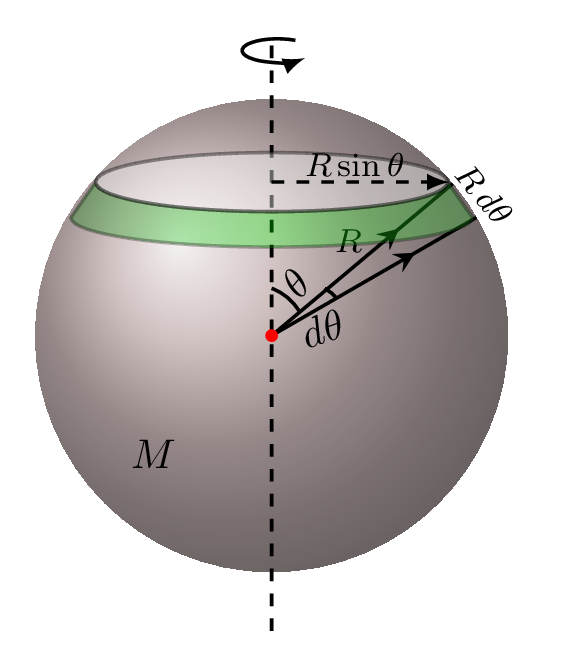
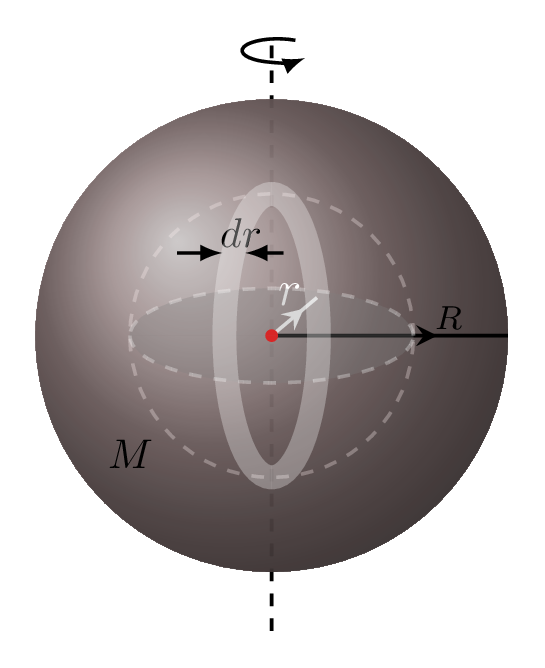
Subsubsection 7.1.9.1 Moment of inertia of a hollow sphere about its diameter
Consider an elementary ring of radius \(r\) with thickness \(\,dr\) in a hollow sphere of mass \(M\) and radius \(R\) [Figure 7.1.12.(a)], then the moment of inertia of this ring about its center of mass can be given as
\begin{equation*}
\,dI=\,dm\,r^{2} = \,dm(R\sin\theta)^{2}=\left[\frac{M}{4\pi R^{2}}\right]\left(2\pi R\sin\theta\right) R\,d\theta (R\sin\theta)^{2}
\end{equation*}
mass of a ring = (mass per unit area of sphere) (area of a ring)
Therefore the moment of inertia of a hollow sphere about its diameter is given by
\begin{equation}
\therefore\quad I =\int\,dI = \frac{MR^{2}}{2}\int\limits_{0}^{\pi}\sin^{3}\theta\,d\theta \tag{7.1.1}
\end{equation}
\begin{equation*}
Now, \quad \sin^{3}\theta = \frac{3\sin\theta-\sin 3\theta}{4}
\end{equation*}
\begin{equation*}
\therefore\quad I = \frac{MR^{2}}{2} \frac{1}{4}\left[-3\cos\theta - \frac{\cos3\theta}{3}\right]_{0}^{\pi}
\end{equation*}
\begin{equation*}
=\frac{1}{8}MR^{2}\left[-3(-1-1)+\frac{1}{3}(-1-1)\right]
\end{equation*}
\begin{equation*}
\therefore\quad I =\frac{1}{8}MR^{2}\left[6-\frac{2}{3}\right]=\frac{16}{3}\times\frac{1}{8}MR^{2}=\frac{2}{3}MR^{2}
\end{equation*}
Subsubsection 7.1.9.2 Moment of inertia of a solid sphere about its diameter
Consider a concentric hollow spherical shell of radius \(r\) and thickness \(\,dr\) in a hollow sphere of mass \(M\) and radius \(R\) [Figure 7.1.12.(b)], then the moment of inertia of this shell about its center of mass is given by
\begin{equation*}
\,dI=\frac{2}{3}\,dm\,r^{2} = \frac{2}{3}\left(\frac{M}{\frac{4}{3}\pi R^{3}}\right)\left(4\pi r^{2}\,dr\right)\,r^{2}
\end{equation*}
mass of a shell = (mass per unit volume of sphere) (volume of a shell)
Therefore the moment of inertia of a solid sphere about its diameter is given by
\begin{equation*}
\therefore\quad I =\int\,dI = \frac{2M}{R^{3}}\int\limits_{0}^{R}r^{4} \,dr
\end{equation*}
\begin{equation*}
= \frac{2M}{R^{3}}\left(\frac{r^{5}}{5}\right)_{0}^{R} =\frac{2}{5}MR^{2}
\end{equation*}
Note: All the above calculations were made by considering uniform mass distribution of a symmetrical object.
