Subsection 5.2.2 Pulley
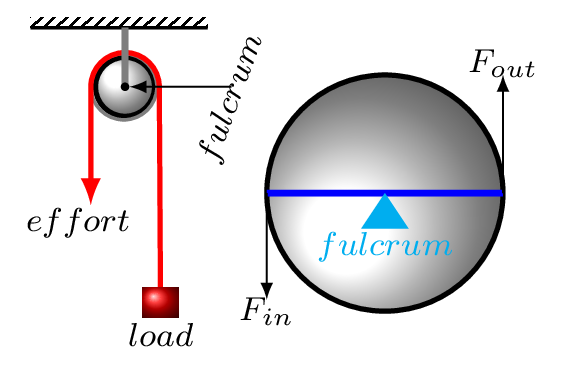
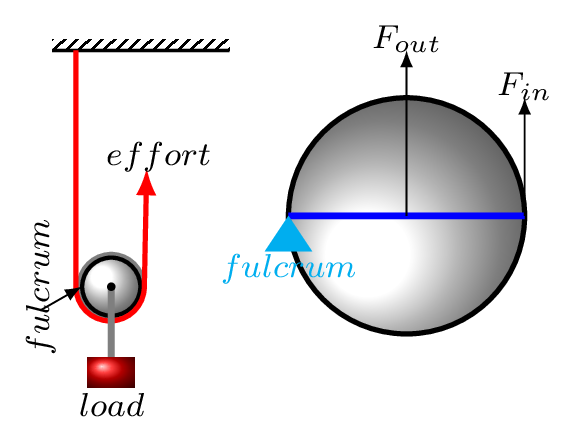
Another type of simple machine is a pulley. The pulley is just a lever in disguise. A single fixed pulley acts like a lever with equal arms. It changes only the direction of the input force. When a person pulls down on the rope, the load is lifted up as shown in Figure 5.2.5.(a). In a single movable pulley, the load can be lifted with an input force that is only half of the load’s true weight Figure 5.2.5.(b).
Subsubsection 5.2.2.1 Mechanical Advantage
Simple machine makes work easier to do. Mechanical advantage is used to quantify how easy to do the work by using simple machine. The number of times input force is multiplied under ideal conditions, i.e., when no friction present, is called an Ideal Mechanical Advantage, IMA.
\begin{equation*}
IMA= \frac{d_{in}}{d_{out}}
\end{equation*}
The number of times input force is multiplied under real world conditions, i.e., when friction is present, is called an Actual Mechanical Advantage, AMA.
\begin{equation*}
AMA = \frac{F_{out}}{F_{in}}
\end{equation*}
Subsubsection 5.2.2.2 Types of Pulley
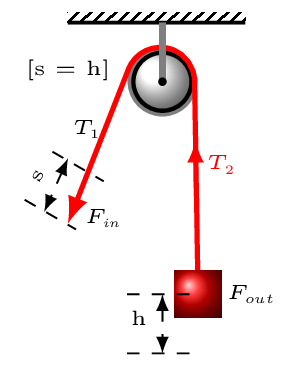
- Single Fixed Pulley: This pulley does not multiply the input force. It does change the direction of the force from up to down [Figure 5.2.6.(a)].\begin{equation*} T_{1}=F_{in}=T_{2}=F_{out} \end{equation*}\begin{equation*} W_{in}=W_{out}\quad \Rightarrow \quad F_{in}d_{in}=F_{out}d_{out} \end{equation*}\begin{equation*} \therefore\quad IMA = \frac{d_{in}}{d_{out}}=\frac{s}{h}=1 \end{equation*}
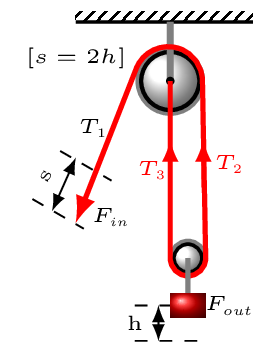
- One Fixed and One Movable Pulley: This pulley does multiply the input force and change the direction of the force as well [Figure 5.2.6.(b)].\begin{equation*} T_{1}=T_{2}=T_{3}=\frac{F_{out}}{2} \end{equation*}\begin{equation*} \text{and}\quad F_{in}=T_{1} \end{equation*}\begin{equation*} W_{in}=W_{out}\quad \Rightarrow \quad F_{in}d_{in}=F_{out}d_{out} \end{equation*}\begin{equation*} \frac{F_{out}}{F_{in}}= \frac{2T_{1}}{T_{1}}=\frac{d_{in}}{d_{out}} \end{equation*}\begin{equation*} d_{in}=2d_{out} \end{equation*}\begin{equation*} \therefore\quad IMA = \frac{d_{in}}{d_{out}}=\frac{s}{h}=\frac{2h}{h} =2 \end{equation*}
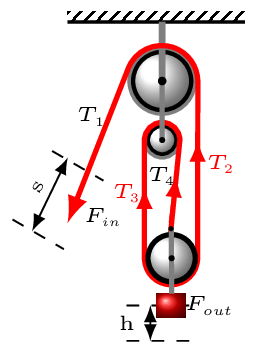
- Two Fixed and One Movable Pulley: This pulley change the direction of the force, and it also multiplies it [Figure 5.2.6.(c)].\begin{equation*} T_{1}=T_{2}=T_{3}=T_{4}=\frac{F_{out}}{3} \end{equation*}\begin{equation*} \text{and}\quad F_{in}=T_{1} \end{equation*}\begin{equation*} W_{in}=W_{out} \end{equation*}\begin{equation*} F_{in}d_{in}=F_{out}d_{out} \end{equation*}\begin{equation*} \frac{F_{out}}{F_{in}}= \frac{3T_{1}}{T_{1}}=\frac{d_{in}}{d_{out}} \end{equation*}\begin{equation*} d_{in}=3d_{out} \end{equation*}\begin{equation*} \therefore\quad IMA = \frac{d_{in}}{d_{out}}=\frac{s}{h}=\frac{3h}{h} =3 \end{equation*}
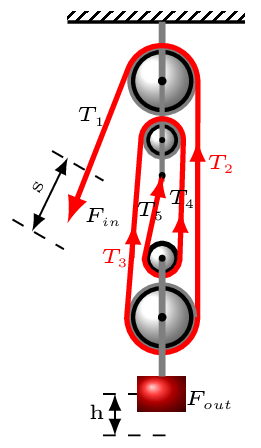
- Two Fixed and Two Movable Pulley: This pulley change the direction of the force, and it also multiplies it [Figure 5.2.6.(d)].\begin{equation*} T_{1}=T_{2}=T_{3}=T_{4}=T_{5}=\frac{F_{out}}{4} \end{equation*}\begin{equation*} \text{and} \quad F_{in}=T_{1} \end{equation*}\begin{equation*} W_{in}=W_{out} \quad \Rightarrow \quad F_{in}d_{in}=F_{out}d_{out} \end{equation*}\begin{equation*} \frac{F_{out}}{F_{in}}= \frac{4T_{1}}{T_{1}}=\frac{d_{in}}{d_{out}} \end{equation*}\begin{equation*} d_{in}=4d_{out} \end{equation*}\begin{equation*} \therefore\quad IMA = \frac{d_{in}}{d_{out}}=\frac{s}{h}=\frac{4h}{h} =4 \end{equation*}Suppose the load, \(F_{out} =100\,N,\) then the actual input force would be a little greater than the ideal value of \(F_{in}\text{,}\) say 25N in this case, It might be 30 N. The extra 5 newtons is used to overcome the friction.\begin{equation*} W_{in} \gt W_{out}\qquad \text{or,}\quad F_{in} d_{in} \gt F_{out}d_{out} \end{equation*}\begin{equation*} \therefore AMA = \frac{F_{out}}{F_{in}} =\frac{100}{30} =3.33 \end{equation*}The AMA will always be less than the IMA.
The value of IMA in case of pulley can be easily determined by just looking at the picture. Just count the number of strands of rope that directly support the load. In Figure 5.2.6.(d), there is 4 strands of rope supporting the load,
\begin{equation*}
\therefore, IMA = 4.
\end{equation*}
In Figure 5.2.6.(c), 3 strands of rope supporting the load,
\begin{equation*}
\therefore IMA=3.
\end{equation*}
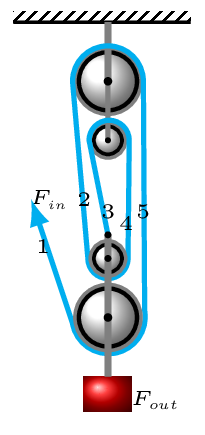
In Figure 5.2.6.(e), there is 5 strands supporting the load,
\begin{equation*}
\therefore\quad IMA = 5.
\end{equation*}
Besides lever and pulley, there are four other simple machines. They are the screw, the inclined plane, the wedge, and the wheel & axle.
Efficiency.
\begin{equation*}
\varepsilon = \frac{W_{out}}{W_{in}} =\frac{P_{out}}{P_{in}} = \frac{AMA}{IMA}
\end{equation*}
