Section 4.11 Torque
The rotational effect of force is called a torque. It is a physical quantity that changes the object’s state of rotational motion. It is a rotational analog of force in a linear motion. It depends on the magnitude, direction and location of force that is acting on the body. Imagine we try to push a door to open it. How much push we apply to rotate the door depends on how far from the hinges (the pivot point \(O\)) and the direction we are applying a force. The closer we are to the hinges (the smaller r), the harder it is to push. The torque we created on the door is smaller when we push it near the hinge than it would be away from its hinges.
Consider a force \(F\) acts on an object at a distance \(r\) from the point of pivot \(O\) in such a way that the object rotates about the point \(O\text{,}\) then the magnitude of the torque \(\Gamma\) about the axis of rotation through \(O\) is given by
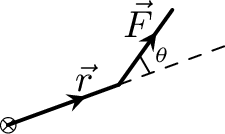
From Figure 4.11.1.(a),
\begin{equation*}
\vec{\Gamma} =\vec{r}\times\vec{F}=rF\sin\theta \hat{n},
\end{equation*}
where \(\hat{n}\) is the direction of torque acting on an object.
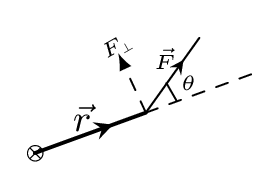
From Figure 4.11.1.(b),
\begin{equation*}
\Gamma =r(F\sin\theta) = rF_\perp,
\end{equation*}
i.e., Torque = radius \(\times \) (perpendicular component of force).
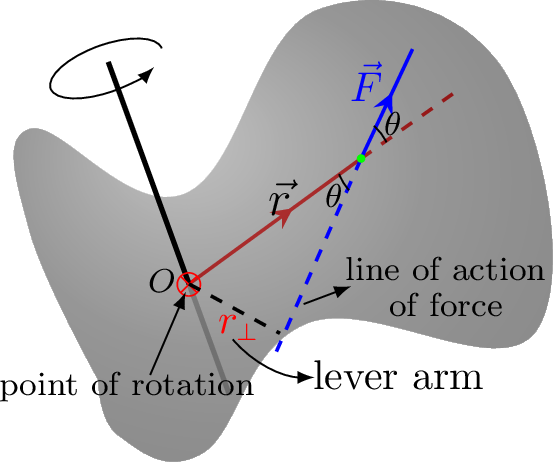
From Figure 4.11.1.(c),
\begin{equation*}
\Gamma =F(r\sin\theta) = Fr_\perp,
\end{equation*}
i.e., Torque = force \(\times\) (lever arm).
The shortest distance between line of action of force to the point of rotation of a body is called the lever arm or moment arm. Torque is maximum when force and lever arm are perpendicularly to each other. There will be no torque if a force is applied at the pivot point (point of rotation) since the moment arm would be zero (r = 0). It is a vector quantity and its direction is always perpendicular to the plane describes by a lever arm and a force. Our right hand can be useful to find the direction of torque. Stretch your right hand fingures in the direction of lever arm then curl them in a direction of force. Now thumb must be oriented in the direction of torque. Since torque is associated with three dimensional case but the motion of object we consider here is only in a plane we make it simple by using the following convention.
Torque is taken as positive (\(+ve\)) if it tends to rotate the object counterclockwise, and negative (\(-ve\)) if it tends to rotate the object clockwise. The direction of torque and the direction of rotation can be remembered using the right-hand thumb’s rule. The thumb of right hand gives the direction of torque, if the fingers curled along the direction of rotation of the body. The torque vector is perpendicular to \(\vec{r}\) and \(\vec{F}\text{.}\) When torque points into the screen, the rotation is clockwise and when it points out of the screen, the rotation is counter-clockwise. There may be more than one forces acting on an object, and each of these forces may act on different points on the object. Then, each force will cause a torque. The net torque is the sum of the individual torques.
\begin{equation*}
\Gamma=\sum_{i} \Gamma_{i}
\end{equation*}
