Subsection 2.1.1 Components of a Vector:
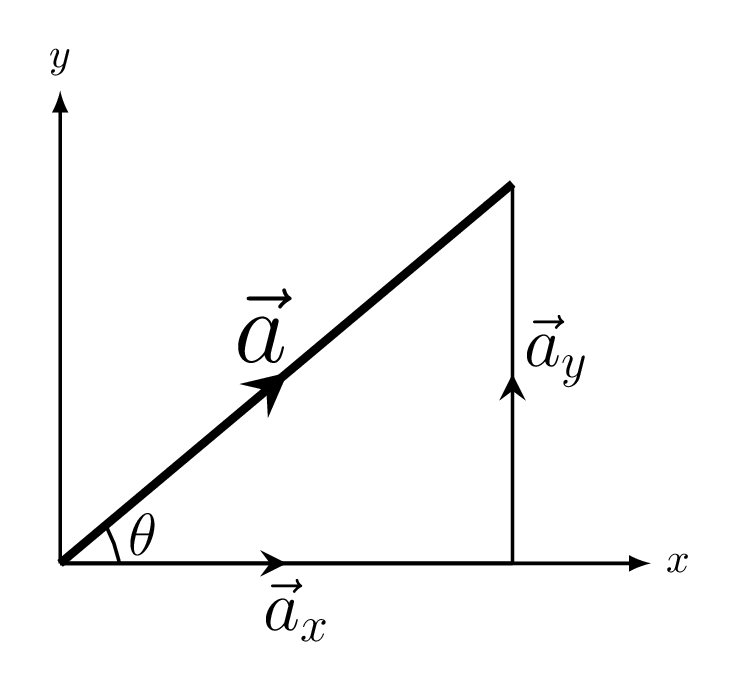
A vector \(\vec{r}\) can be resolved into its components in a coordinate system. Suppose a vector \(\vec{a}\) is lying on the xy-plane as shown in Figure 2.1.2.(a), then its x- and y- components are given as \(\vec{a_{x}}\) and \(\vec{a_{y}}\text{,}\) respectively. Hence the vector \(\vec{a} \) can be written as
\begin{equation*}
\vec{a} = \vec{a_{x}} + \vec{a_{y}} = a_{x}\hat{i} + a_{y}\hat{j} =a\cos\theta \hat{i}+a\sin\theta \hat{j}
\end{equation*}
where \(a_{x} =a\cos\theta\) and \(a_{y}=a\sin\theta \) are the magnitude of vector components \(\vec{a_{x}}\) and \(\vec{a_{y}}\text{,}\) respectively. The magnitude of vector \(\vec{a} \) is given by
\begin{equation*}
a^{2}= a^{2}_{x}+a^{2}_{y} \quad \Rightarrow |\vec{a}|=\sqrt{a^{2}_{x}+a^{2}_{y}}.
\end{equation*}
The direction of \(\vec{a}\) can be obtained by
\begin{equation*}
\tan\theta =\frac{a_{y}}{a_{x}} \quad \Rightarrow \theta=\tan^{-1}\frac{a_{y}}{a_{x}}.
\end{equation*}
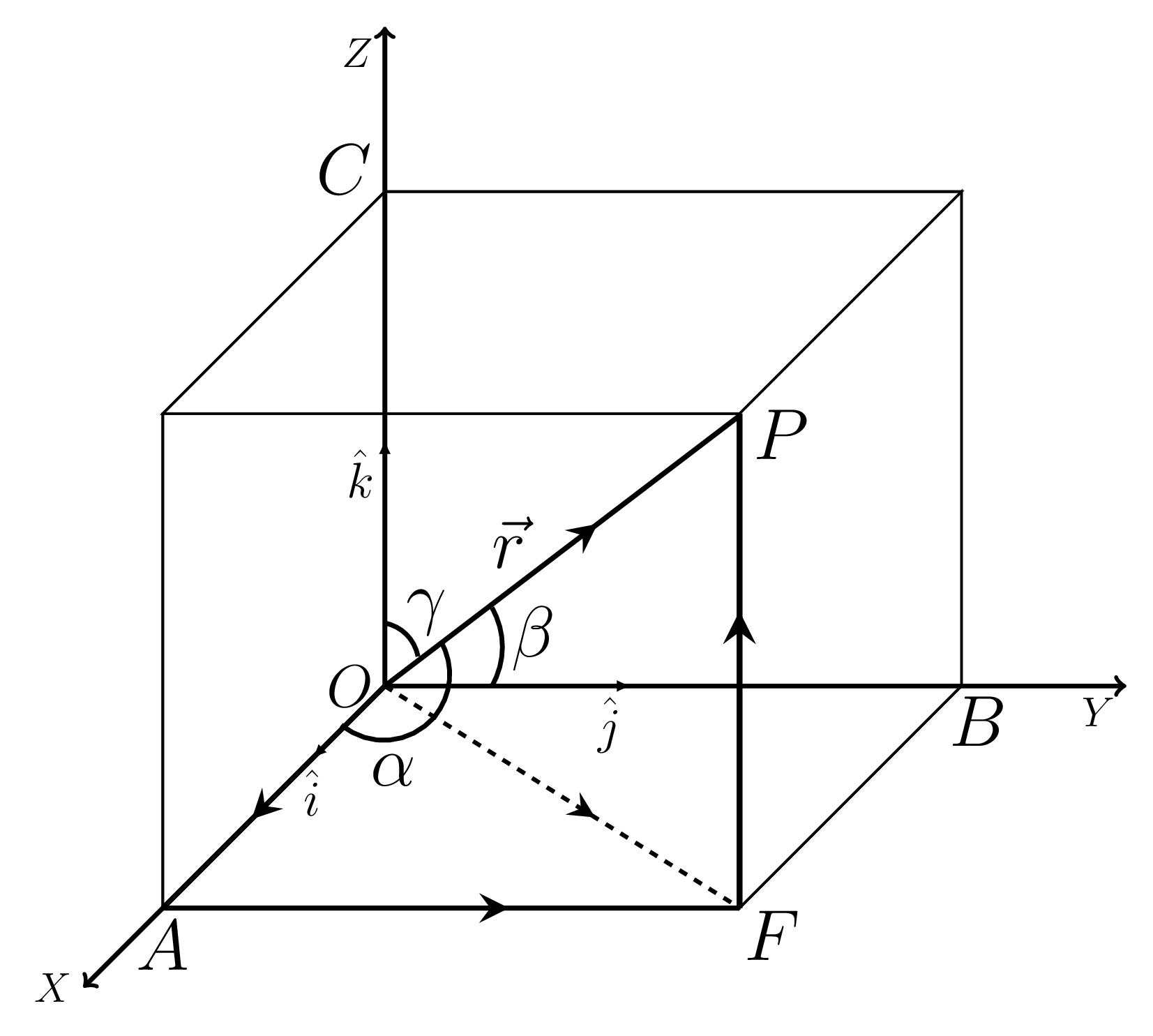
Let the diagonal vector of a parallelopiped, \(\vec{OP} = \vec{r}\) is described by a coordinate (x,y,z) in a rectangular system as shown in Figure 2.1.2.(b) and \(\hat{i}\text{,}\) \(\hat{j}\text{,}\) and \(\hat{k}\) are the unit vectors along \(OX\text{,}\) \(OY\text{,}\) and \(OZ\) axes, respectively then \(\vec{OA} = x \hat{i}\text{,}\) \(\vec{OB} = y \hat{j}\text{,}\) and \(\vec{OC} = z \hat{k}\) are the rectangular components of \(\vec{r}\text{.}\) Now,
\begin{equation}
\vec{r} = \vec{OP} = (\vec{OF} + \vec{FP}) \tag{2.1.1}
\end{equation}
\begin{equation}
\text{and} \quad \vec{OF} = \vec{OA} + \vec{AF} \tag{2.1.2}
\end{equation}
\begin{equation}
\therefore \quad \vec{r} = \vec{OA} + \vec{OB} + \vec{OC} = x \hat{i} + y \hat{j} + z \hat{k} \tag{2.1.3}
\end{equation}
\begin{equation*}
\because\quad \vec{AF}= \vec{OB}; \quad \vec{FP} = \vec{OC}
\end{equation*}
If \(\vec{OP}\) makes angles \(\alpha\text{,}\) \(\beta\text{,}\) and \(\gamma\) with OX, OY, and OZ axes, respectively then \(x=r\cos\alpha\text{,}\) \(y=r\cos\beta\text{,}\) and \(z=r\cos\gamma\text{.}\)
