Subsection 10.5.5 Gas Laws
From equation of state,
\begin{equation*}
pV = nRT,
\end{equation*}
and if T of a gas remains constant, then
\begin{equation*}
pV=constant.
\end{equation*}
\begin{equation*}
\text{or,}\quad p\propto\frac{1}{V}
\end{equation*}
\begin{equation*}
\text{or,} \quad p_{i}V_{i}=p_{f}V_{f}
\end{equation*}
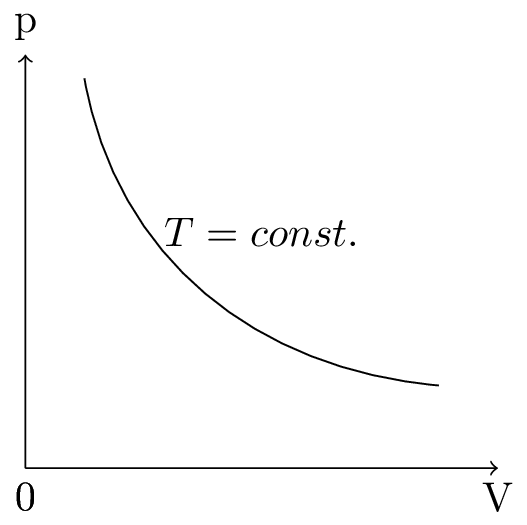
This is called a Boyle’s law, the pV diagram of Boyle’s law is shown in Figure 10.5.3.(a). At constant temperature, the average force of each particle striking the surface will be the same. But as the area of the container has increased, there will be fewer of these collisions per unit area and the pressure will decrease. Volume is inversely proportional to pressure, if the number of particles and the temperature are constant.
If pressure remains constant, then
\begin{equation*}
\frac{V}{T} = constant.
\end{equation*}
\begin{equation*}
\text{or,}\quad V\propto T
\end{equation*}
\begin{equation*}
\text{or,} \quad \frac{V_{i}}{T_{i}}=\frac{V_{f}}{T_{f}}
\end{equation*}
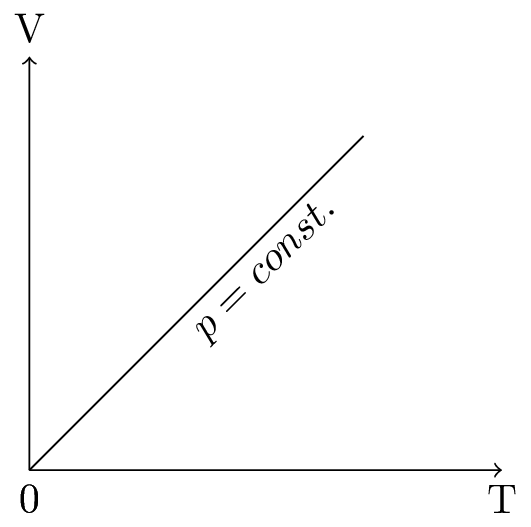
This is called a Charle’s law, the \(V \sim T\) diagram is shown in Figure 10.5.3.(b). To keep the pressure constant as the volume increases is to raise the average force that each particle exerts on the surface. This happens when the temperature is increased. So if the number of particles and the pressure are constant, temperature is proportional to the volume.
If volume remains constant, then
\begin{equation*}
\frac{p}{T} = constant.
\end{equation*}
\begin{equation*}
\text{or,}\quad p\propto T
\end{equation*}
\begin{equation*}
\text{or,} \quad \frac{p_{i}}{T_{i}}=\frac{p_{f}}{T_{f}}
\end{equation*}
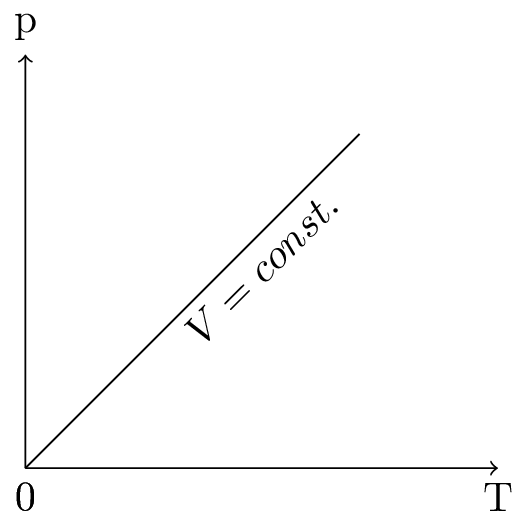
This is called a pressure law (or Gay-Lussac’s law), the \(V \sim T\) diagram is shown in Figure 10.5.3.(c). As the temperature increases, the average kinetic energy increases as does the velocity of the gas particles hitting the walls of the container. The force exerted by the particles per unit of area on the container is the pressure, so as the temperature increases the pressure must also increase. Pressure is proportional to temperature, if the number of particles and the volume of the container are constant.
Avogadro’s law: Volume of a gas is directly proportional to the amount of gas at a constant temperature and pressure, i.e.,
\begin{equation*}
V\propto n.
\end{equation*}
The Combined Gas Law: If number moles of a gas only remains constant, then we have -
\begin{equation*}
\frac{pV}{T}=constant.
\end{equation*}
The volume of a given amount of gas is proportional to the ratio of its absolute temperature and its pressure, i.e.,
\begin{equation*}
V\propto\frac{T}{p}.
\end{equation*}
