Subsection 6.2.1 Polar Coordinates
Before we go to kepler’s laws derivation lets first recall polar coordinates.
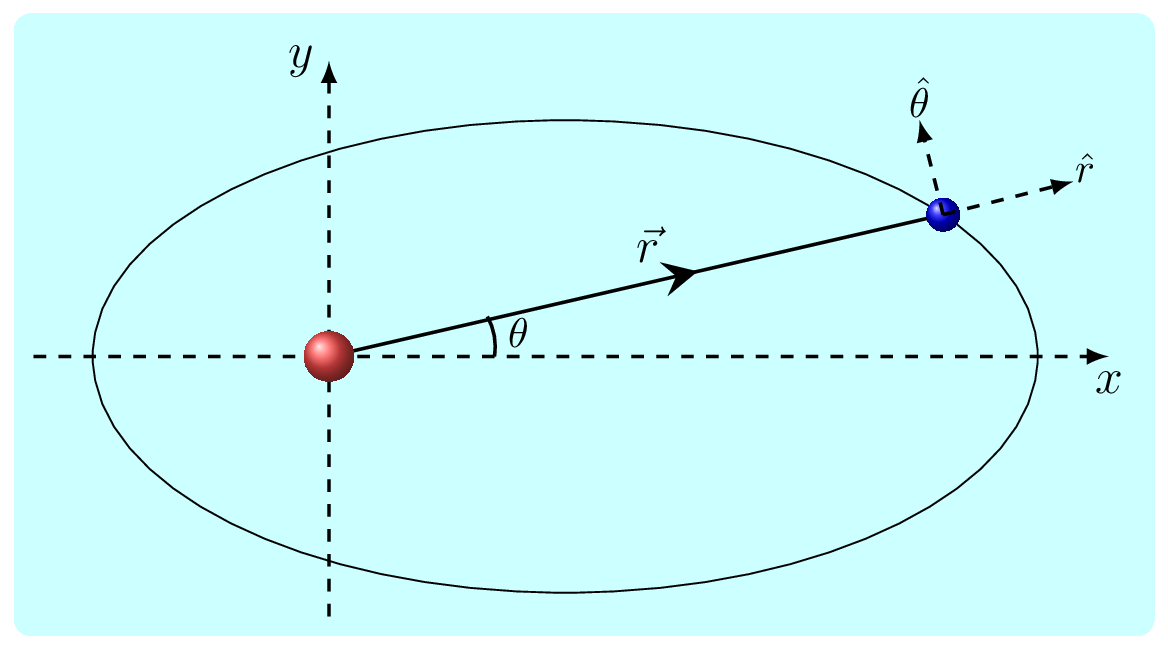
Here, \(\hat{r}=\hat{r}(\theta)\)
\begin{equation}
\hat{r} = \hat{x}\cos\theta + \hat{y}\sin\theta\tag{6.2.1}
\end{equation}
and
\begin{equation*}
\frac{\,d\hat{r}}{\,d\theta}=-\hat{x}\sin\theta + \hat{y}\cos\theta
\end{equation*}
Now
\begin{equation*}
\hat{r} \cdot \frac{d\hat{r}}{d\theta} =0
\end{equation*}
\(\Rightarrow \hat{r} \) is perpendicular on \(\frac{d\hat{r}}{d\theta}.\)
Therefore, we call
\begin{equation}
\frac{\,d\hat{r}}{\,d\theta}=-\hat{x}\sin\theta + \hat{y}\cos\theta =\hat{\theta}\tag{6.2.2}
\end{equation}
Also, \(\hat{\theta}=\hat{\theta}(\theta)\)
and,
\begin{equation}
\frac{\,d\hat{\theta}}{\,d\theta}=-\hat{x}\cos\theta - \hat{y}\sin\theta =-\hat{r}\tag{6.2.3}
\end{equation}
Now,
\begin{align*}
\vec{v}\amp = \frac{\,d\vec{r}}{\,dt}\\
\amp = \frac{\,d}{\,dt}(r\hat{r}) \\
\amp =\dot{r}\hat{r} + r \frac{\,d\hat{r}}{\,dt}\\
\amp =\dot{r} \hat{r} + r \frac{\,d\hat{r}}{\,d\theta} \frac{\,d\theta}{\,dt}
\end{align*}
\(\because \theta =\theta(t)\)
\begin{equation}
\therefore \vec{v} = \dot{r} \hat{r} +r\dot{\theta}\hat{\theta} = v_r +v_{\theta}\tag{6.2.4}
\end{equation}
Again,
\begin{align*}
\vec{a}\amp =\frac{\,d\vec{v}}{\,dt} \\
\amp = \frac{\,d}{\,dt}( \dot{r} \hat{r} +r\dot{\theta}\hat{\theta}) \\
\amp =\ddot{r} \hat{r} +\dot{r}\frac{\,d\hat{r}}{\,dt} + \dot{r}\dot{\theta}\hat{\theta} + r\ddot{\theta}\hat{\theta} + r\dot{\theta}\frac{\,d\hat{\theta}}{\,dt}\\
\amp = \ddot{r} \hat{r} +\dot{r}\frac{\,d\hat{r}}{\,d\theta} \frac{\,d\theta}{\,dt}
+ \dot{r}\dot{\theta}\hat{\theta} + r\ddot{\theta}\hat{\theta} + r\dot{\theta}\frac{\,d\hat{\theta}}{\,d\theta} \frac{\,d\theta}{\,dt}\\
\amp = \ddot{r} \hat{r} + 2\dot{r}\dot{\theta}\hat{\theta}+r\ddot{\theta}\hat{\theta}-r\dot{\theta}^2\hat{r}
\end{align*}
\begin{equation}
\therefore \vec{a} = (\ddot{r} -r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta}+r\ddot{\theta})\hat{\theta} = a_r +a_{\theta}\tag{6.2.5}
\end{equation}
