Subsection 7.1.4 Moment of Inertia of a Rod
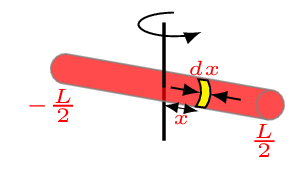
Subsubsection 7.1.4.1 About an axis passing through its center of mass and perpendicular to its plane
The moment of inertia of a rod of length \(L\) and mass \(M\) about an axis passing through its center of mass [Figure 7.1.5.(a)] can be find by considering an elementary mass \(\,dm \) of a rod of infinitesimal thickness \(\,dx\) at a distance \(x\) from the axis of rotation, then the moment of inertia of this elementary mass (strip) is given by
\begin{equation*}
\,dI = \,dm x^{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad I = \int \,dI = \int\limits_{-\frac{L}{2}}^{\frac{L}{2}}\left(\frac{M}{L}\,dx\right)x^{2}
\end{equation*}
\begin{equation*}
\because \quad \,dm = \left(\frac{M}{L}\,dx\right)
\end{equation*}
\begin{equation*}
i.e., \text{mass of a strip} =(\text{mass per unit length of a rod})\cdot (\text{length of a strip})
\end{equation*}
\begin{equation*}
\therefore\quad I =\frac{M}{L} \int\limits_{-\frac{L}{2}}^{\frac{L}{2}} x^{2} \,dx
\end{equation*}
\begin{equation*}
= \frac{M}{L}\left(\frac{x^{3}}{3}\right)_{-\frac{L}{2}}^{\frac{L}{2}}
\end{equation*}
\begin{equation*}
= \frac{M}{3L}\left[\left(\frac{L}{2}\right)^{3}-\left(-\frac{L}{2}\right)^{3}\right]
\end{equation*}
\begin{equation*}
=\frac{2M}{3L}\left(\frac{L^{3}}{8}\right)=\frac{1}{12}ML^{2}
\end{equation*}
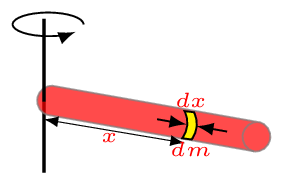
Subsubsection 7.1.4.2 About an axis passing through its one edge and perpendicular to its plane
Consider a rod of length \(L\) and mass \(M\) is rotating about an axis passing through one of its edges as shown in Figure 7.1.5.(b). To find the moment of inertia of such a rod consider an elementary mass \(\,dm \) of a rod of infinitesimal thickness \(\,dx\) at a distance \(x\) from the axis of rotation, then the moment of inertia of this elementary mass is given by
\begin{equation*}
\,dI = \,dm x^{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad I = \int \,dI = \int\limits_{0}^{L}\left(\frac{M}{L}\,dx\right)x^{2}
\end{equation*}
\begin{equation*}
\therefore\quad I =\frac{M}{L}\int\limits_{0}^{L} x^{2} \,dx
\end{equation*}
\begin{equation*}
= \frac{M}{L}\left(\frac{x^{3}}{3}\right)_{0}^{L}
\end{equation*}
\begin{equation*}
= \frac{M}{3L}(L^{3}-0)=\frac{1}{3}ML^{2}
\end{equation*}
Alternative Using parallel axis theorem,
\begin{equation*}
I_{edge} = I_{cm}+Md^{2}
\end{equation*}
\begin{equation*}
=\frac{1}{12}ML^{2} +M\left(\frac{L}{2}\right)^{2}=\frac{1}{3}ML^{2}
\end{equation*}
here, \(d\) is the distance between axis of rotation and an axis through center of mass of a rod.
Subsubsection 7.1.4.3 About an axis passing along its length and through the center of mass
If the rod is negligibly thin (slender rod), then \(I_{z}=0\text{,}\) otherwise depends upon of its shape, its moment of inertia can be obtained similar to that for a solid cylinder
\begin{equation*}
I=\frac{1}{2}mr^{2}
\end{equation*}
or as for a rectangular prism
\begin{equation*}
I_{z}=\frac{1}{12}m(x^{2}+y^{2})
\end{equation*}
