Section 7.1 Moment of Inertia
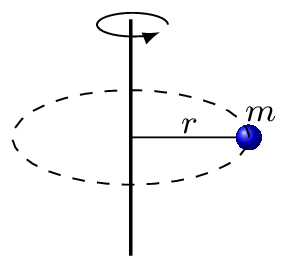
Moment of inertia is a property of a material during rotation. It is a measure of sluggishness (resistance to any changes) in object’s rotational motion. Moment of inertia depends on the shape, mass distribution, and axis of rotation of the object. It is a rotational analog of a mass for linear motion. For a point mass the moment of inertia is just the product of mass and the square of perpendicular distance to the rotation axis. If a point object has a mass \(m\) and is rotating about an axis then its moment of inertia, \(I\) is given by \(I=mr^{2}.\) where \(r\) is a distance of the object from the axis of rotation [Figure 7.1.1.(a)]. If there are an infinite number of point objects each at a distance \(r_{i}\) are rotating about an axis, then the moment of inertia (M.I) of these discrete objects are given as
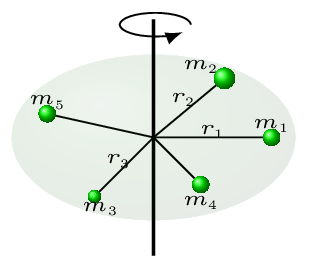

\begin{equation*}
I=\sum\limits_{i=1}^{n} m_{i}r^{2}_{i} = m_{1} r^{2}_{1} + m_{2} r_{2}^{2}+\cdots ,
\end{equation*}
as shown in Figure 7.1.1.(b). An extended object consists of a continuous distribution of mass at a continually varying distance from the axis of rotation, its moment of inertia can be written as,
\begin{equation*}
I=\int\,dI=\int\limits_{0}^{M} r^{2}\,dm
\end{equation*}
where \(\,dm\) is a differential (infinitely small) mass of the object [Figure 7.1.1.(c)] and \(r\) is a distance of this differential mass from axis of rotation.
