Section 6.1 Newton’s Law of Gravitation
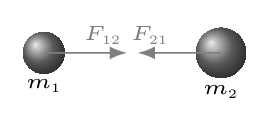
Newton observed that when an object, such as an apple, was released near the surface of the earth, it was accelerated toward the earth. Since the cause of such acceleration is an unbalanced force, there must be a force pulling that object toward the earth. On this basis he came up with an idea called Newton’s Law of Universal Gravitation. It states that any two masses in the universe attract each other with a force that is directly proportional to the product of the masses and inversely proportional to the square of the distance between them. Mathematically,
\begin{equation*}
F \varpropto \frac{m_{1}m_{2}}{r^{2}}
\end{equation*}
\begin{equation*}
\text{or,}\quad F =G \frac{m_{1}m_{2}}{r^{2}}
\end{equation*}
Where \(m_{1}\) and \(m_{2}\) are masses of two objects, \(r\) is the distance between them, and \(G = 6.67 \times 10^{-11} N.m^{2}/kg^{2}\text{,}\) is the proportionality constant, also called the universal gravitational constant. The value of G was first measured by Sir Henry Cavendish experimentally in 1798. The force \(F_{12}\) is the force on mass 1 due to mass 2, the force \(F_{21}\) is the force on mass 2 due to mass 1, and they are equal and opposite [Figure 6.1.1].
