Subsection 6.1.3 Orbital Velocity of a Satelite
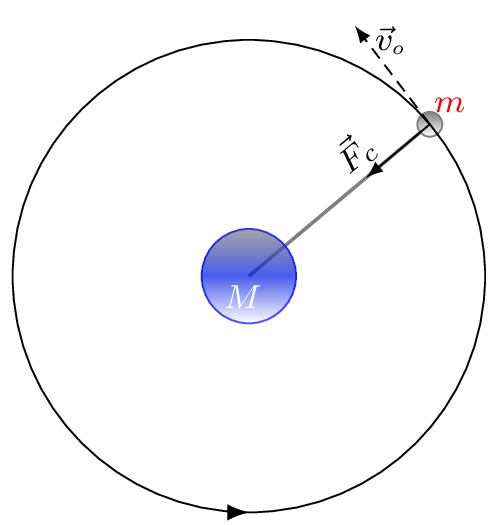
The velocity of a satellite in its orbit around the planet is called the orbital velocity, \(v_{o}\text{.}\) To move in a circular track an object must need a centripetal force which is provided by the force of gravity between the object and the planet. i.e.,
\begin{equation*}
F_{c} = F_{g} \quad \Rightarrow\quad \frac{mv^{2}_{o}}{r}=G\frac{Mm}{r^{2}}
\end{equation*}
\begin{equation*}
\therefore v_{o} = \sqrt{\frac{GM}{r}} =\sqrt{\frac{GM}{R+h}}
\end{equation*}
Where \(r=R+h \text{,}\) \(m\text{,}\) and \(M\) are distance of a satellite (object), mass of a satellite, and mass of the planet, respectively. \(R\) is radius of the planet, \(G\) is universal gravitational constant, and \(h\) is the altitude of the satellite from the surface of the planet.
