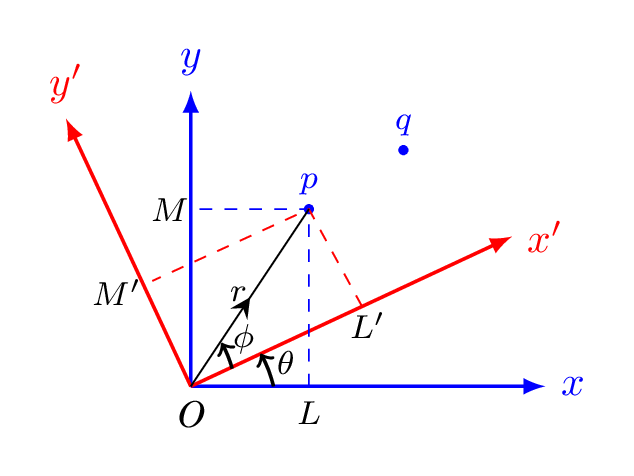
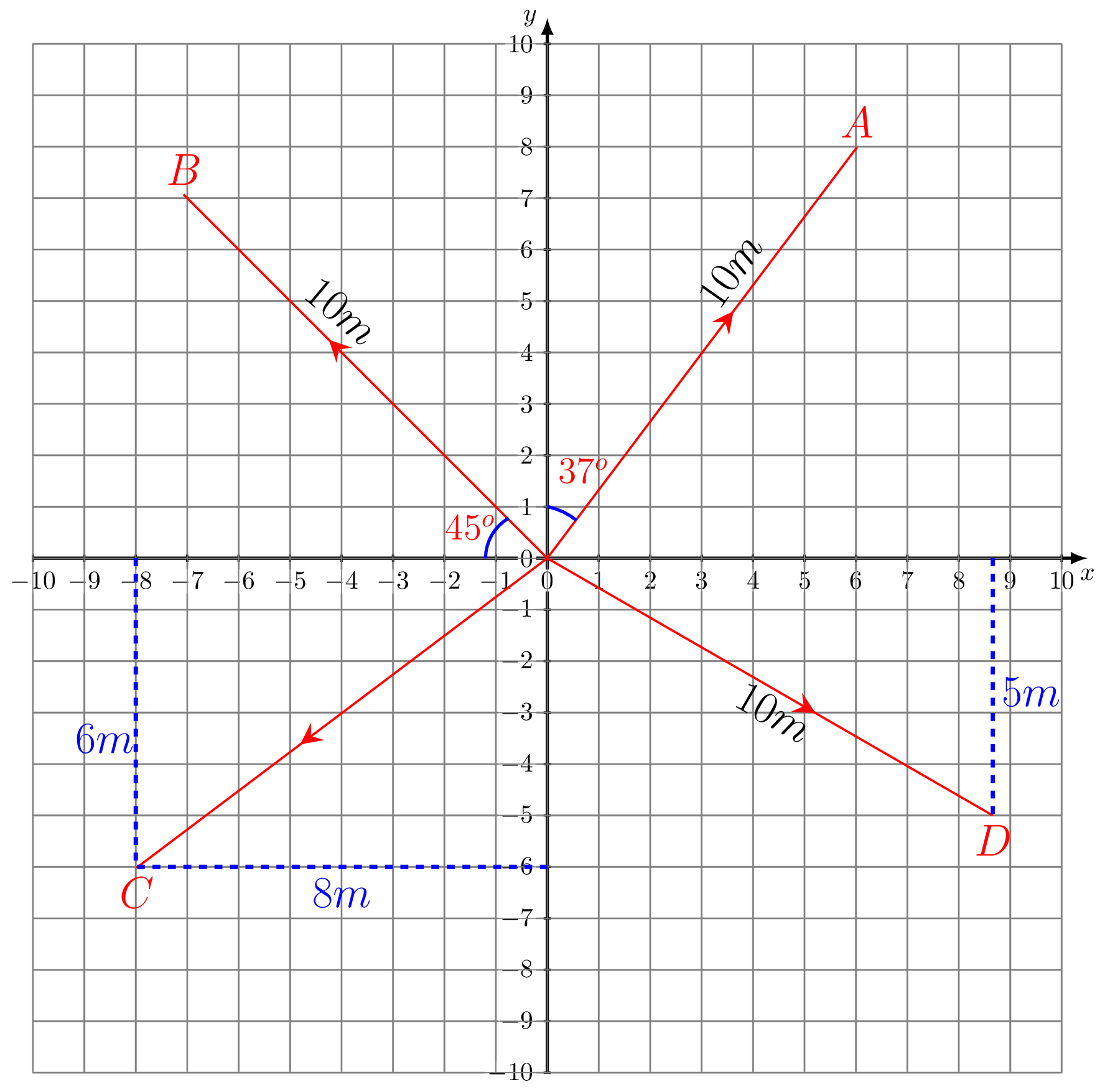
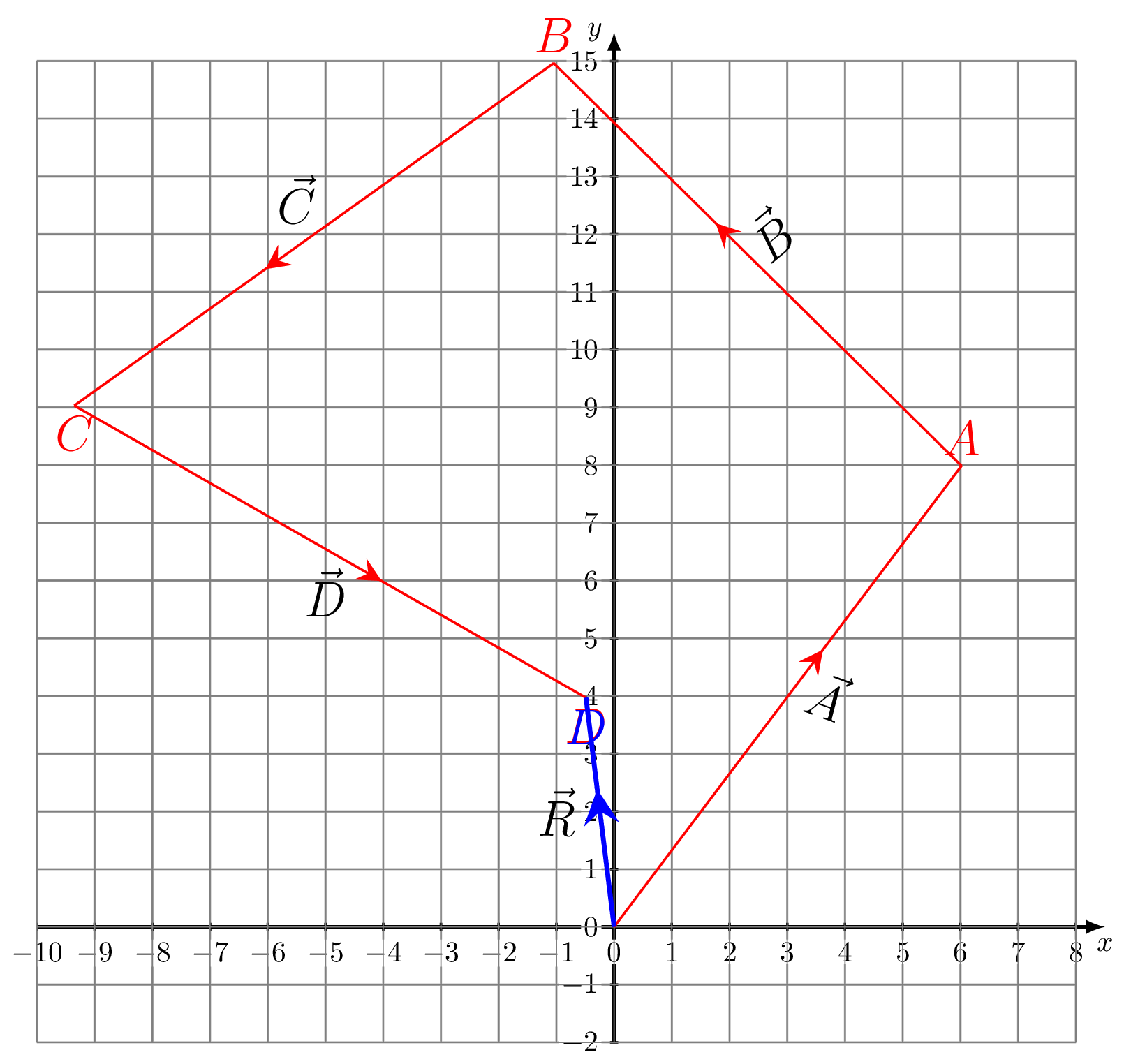
Let p and q be two points in space. Now from figure,
we have -
\begin{equation*}
x'=OL'=r\cos\phi
\end{equation*}
\begin{equation*}
\text{and} \quad y'= PL'=r\sin\phi\text{.}
\end{equation*}
\begin{equation*}
\text{Also} \quad x =OL=r\cos (\theta+\phi)
\end{equation*}
\begin{equation*}
\text{and} \quad y= PL=r\sin (\theta+\phi)
\end{equation*}
\begin{equation*}
\text{Now,} \quad x=r(\cos\theta\cos\phi-\sin\theta\sin\phi)=r\cos\phi\cos\theta-r\sin\phi\sin\theta
\end{equation*}
\begin{equation*}
\therefore\quad x = x'\cos\theta -y'\sin\theta
\end{equation*}
\begin{equation*}
\text{Again,} \quad y=r(\sin\theta\cos\phi-\cos\theta\sin\phi)=r\cos\phi\sin\theta+r\sin\phi\cos\theta
\end{equation*}
\begin{equation*}
\therefore\quad y = x'\sin\theta +y'\cos\theta
\end{equation*}
On solving these equations we get -
\begin{equation*}
x' = x\cos\theta + y\sin\theta
\end{equation*}
\begin{equation*}
\text{and}\quad y' = -x\sin\theta + y\cos\theta
\end{equation*}
The distance between points \(p(x_{1},y_{1})\) and \(q(x_{2},y_{2})\) in xy coordinate system is given by
\begin{equation*}
d=pq=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}
\end{equation*}
\begin{equation*}
=\sqrt{[(x'_{2}-x'_{1})\sin\theta + (y'_{2}-y'_{1})\cos\theta}]^{2} =\sqrt{(x'_{2}-x'_{1})^{2}+ (y'_{2}-y'_{1})^{2}}
\end{equation*}
which is the distance between points \(p(x'_{1},y'_{1})\) and \(q(x'_{2},y'_{2})\) in x’ y’ coordinate system, i.e., the distance between two points is invariant upon the rotation of a coordinate system.
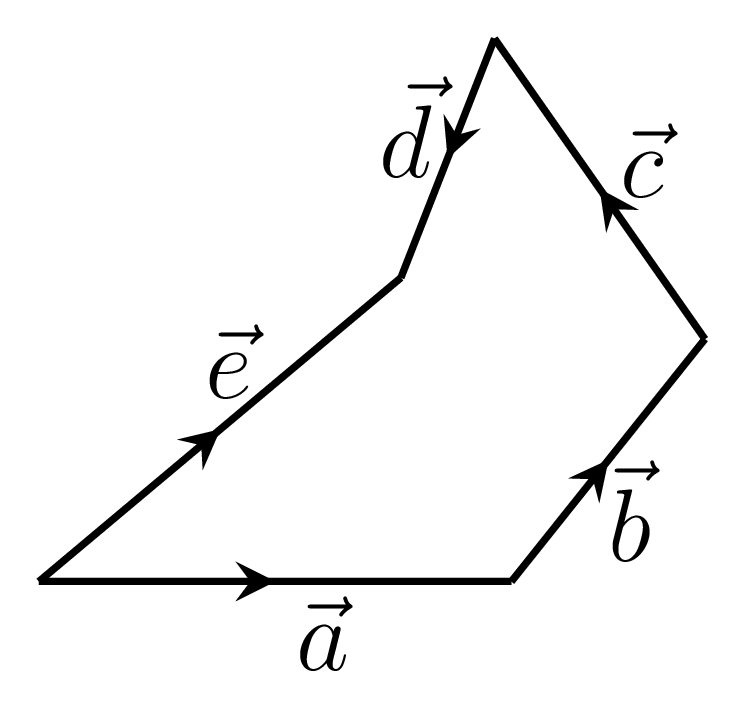
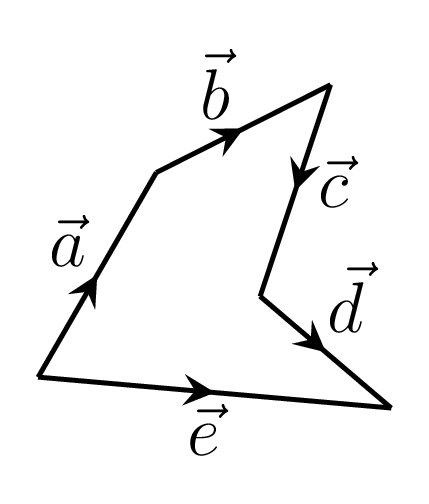
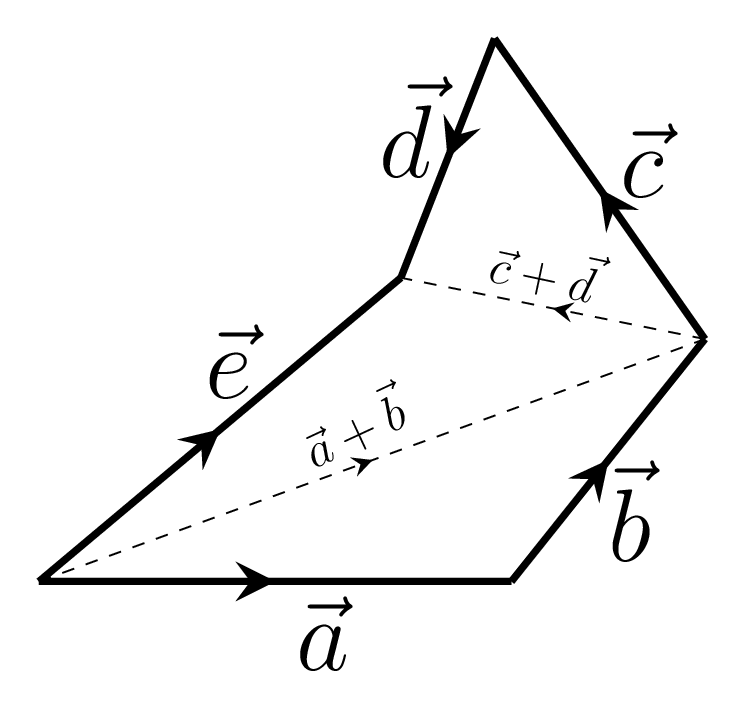
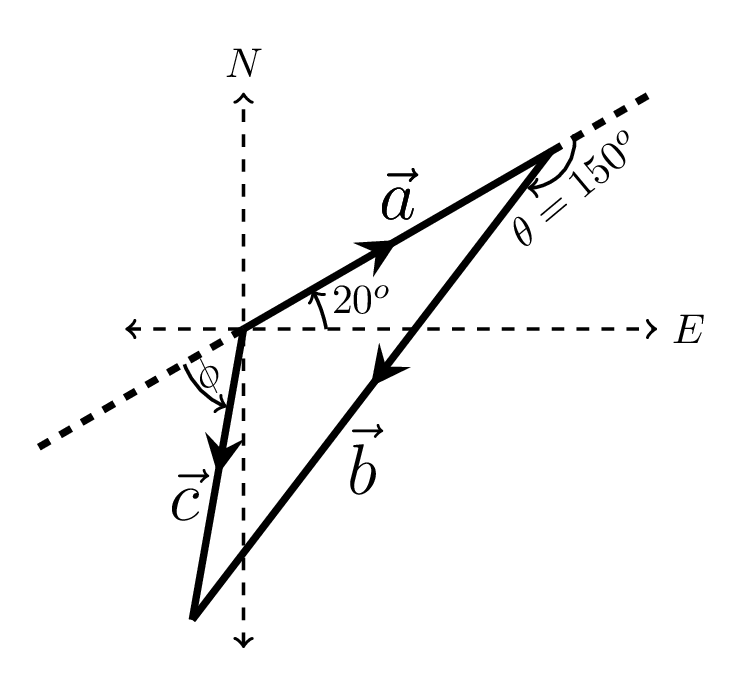
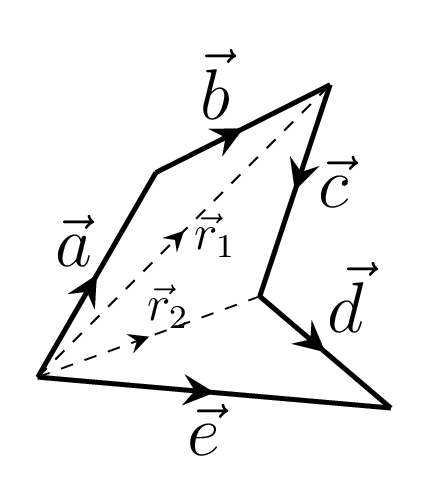 \begin{equation*} \vec{r}_{1}=\vec{a}+\vec{b}, \end{equation*}\begin{equation*} \vec{r}_{2}=\vec{r}_{1}+\vec{c}=(\vec{a}+\vec{b})+\vec{c}, \end{equation*}and\begin{equation*} \vec{e}=\vec{r}_{2}+\vec{d} \end{equation*}\begin{equation*} \therefore \vec{e}=\vec{a}+\vec{b}+\vec{c}+\vec{d} \end{equation*}
\begin{equation*} \vec{r}_{1}=\vec{a}+\vec{b}, \end{equation*}\begin{equation*} \vec{r}_{2}=\vec{r}_{1}+\vec{c}=(\vec{a}+\vec{b})+\vec{c}, \end{equation*}and\begin{equation*} \vec{e}=\vec{r}_{2}+\vec{d} \end{equation*}\begin{equation*} \therefore \vec{e}=\vec{a}+\vec{b}+\vec{c}+\vec{d} \end{equation*}