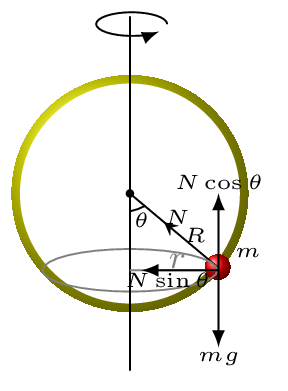
Example 4.9.1.
A car traveling at 80 km/h rounds a curve of radius 100m which is banked for a speed of 50 km/h. What is the minimum coefficient of friction that would keep the car on the road?
Solution.
Given: \(v_{1} = 50\, km/h = 50 \times \frac{5}{18} \frac{m}{s}=13.88 \,m/s r=100\,m\text{,}\) \(v_{2}=80\,km/h=22.22 \,m/s\text{,}\) \(\mu=?\) 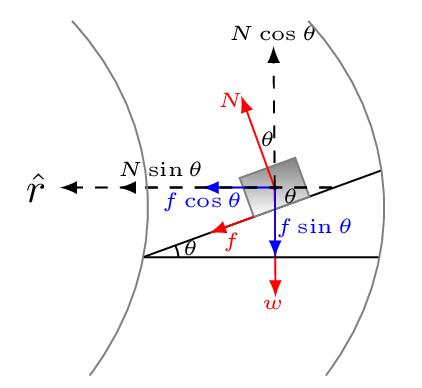

\begin{equation*}
\sum F_{x} = ma
\end{equation*}
\begin{equation}
\text{or,}\quad N\sin\theta+f\cos\theta=\frac{mv_{1}^{2}}{r} \tag{4.9.1}
\end{equation}
\begin{equation*}
\sum F_{y} = 0
\end{equation*}
\begin{equation}
\text{or,}\quad N\cos\theta=f\sin\theta+w \tag{4.9.2}
\end{equation}
\begin{equation}
\text{or,}\quad N\sin\theta=\frac{mv_{1}^{2}}{r} \qquad [\because f=0]\tag{4.9.3}
\end{equation}
\begin{equation}
\text{or,}\quad N\cos\theta=mg \qquad [\because f=0] \tag{4.9.4}
\end{equation}
\begin{equation*}
\text{or,}\quad \tan\theta=\frac{mv^{2}_{1}}{r mg} = \frac{v^{2}_{1}}{r g}=\frac{(13.88)^{2}}{100\times9.8} = 0.196
\end{equation*}
\begin{equation}
\therefore \quad \theta = 11.12^{o}\tag{4.9.5}
\end{equation}
again, from eqn. (4.9.1), if \(f \neq 0\) we have -
\begin{equation}
N\sin\theta+\mu N \cos\theta=\frac{mv_{2}^{2}}{r} \tag{4.9.6}
\end{equation}
\begin{equation*}
\text{or,}\quad N\left[(0.193)+ \mu (0.981)\right] = m\left(\frac{(22.22)^{2}}{100}\right)
\end{equation*}
\begin{equation}
\text{or,}\quad m = 0.2025 N\left[0.193+\mu (0.981)\right] \tag{4.9.7}
\end{equation}
also, from eqn. (4.9.2), if \(f \neq 0\) we have -
\begin{equation}
N\cos\theta-\mu N\sin\theta=mg\tag{4.9.8}
\end{equation}
\begin{equation*}
\text{or,}\quad N (0.981) -\mu N(0.193) =m(9.8)
\end{equation*}
\begin{equation}
\text{or,}\quad m = \frac{N}{9.8}\left[0.981 -\mu (0.193)\right] \tag{4.9.9}
\end{equation}
\begin{equation*}
0.2025 \times 9.8 \left[0.193+\mu (0.981)\right] =\left[0.981 -\mu (0.193)\right]
\end{equation*}
\begin{equation}
\therefore\quad \mu = 0.15 \tag{4.9.10}
\end{equation}