Section 9.5 Surface Tension

A paper clip, a needle, small insects, etc. can float on the surface of water without getting wet [Figure 9.5.1.(a)]. If these events have been observed very closely we can find that water surface behaves as if it is a thin stretched membrane of some kind. The strength of such membrane arises due to intermolecular attraction of the liquid. Liquid molecules try to get as closer as they can. The minimum average distance between the molecules of a liquid occurs when the liquid acquires a spherical shape. A spherical surface possess minimum surface area. Hence a property of a liquid by virtue of which it acquires minimum surface area is called a surface tension. The cohesive nature of a liquid helps resist an external force. If a force \(F\) is acting on a length \(l\) by the liquid surface to balance an external force then, it can be seen that
\begin{equation*}
F\propto l
\end{equation*}
\begin{equation*}
\Rightarrow\quad F = \gamma l
\end{equation*}
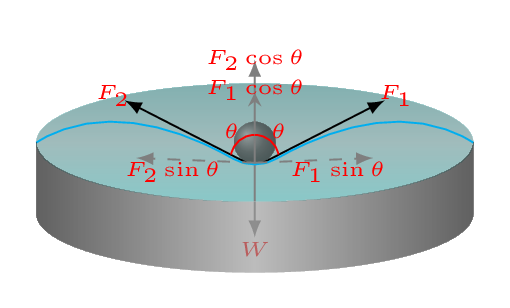
Where \(\gamma \) is a proportionality constant known as coefficient of surface tension, and is a property of the material of the liquid. The force is parallel to the surface and perpendicular to the line. The SI unit of surface tension is N/m. Suppose a needle of length \(l\) is placed of the surface of water very gently, so that it can float. If \(\gamma\) be the surface tension of water then the needle of maximum weight, \(W\) that can be placed on the water surface will be given by -
\begin{equation*}
\sum F = 0
\end{equation*}
\begin{equation*}
\text{or,}\quad F_{1} \cos\theta + F_{2} \cos\theta - W =0
\end{equation*}
\begin{equation*}
\text{or,}\quad \gamma l \cos\theta + \gamma l \cos\theta -W =0
\end{equation*}
\begin{equation*}
\text{or,} \quad W = 2\gamma l cos\theta
\end{equation*}
For maximum weight,
\begin{equation*}
\theta = 0, \qquad \therefore W = 2\gamma l
\end{equation*}
When needle is placed on the water surface, it depresses the water surface which applies forces \(F_{1}\) and \(F_{2}\) on the needle acting along its length on either side so that the needle can be balanced [Figure 9.5.1.(b)].
