Subsection 4.1.3 Friction
Friction is a resistive force that opposes or tends to oppose relative motion between two objects. It is a force that exists between the surfaces of contact of the two objects [Figure 4.1.4.(a)]. If two systems are in contact and stationary relative to each other, then the friction between them is called static friction. This force arises from mechanical interlocking at the microscopic level plus the electrostatic molecular forces that hold the surfaces themselves together. If two systems are in contact and moving relative to one another, then the friction between them is called kinetic friction. This force arises from forming and breaking of microscopic adhesive bonds between atoms on the surfaces plus some mechanical linkage between the small irregularities on the surfaces as shown in Figure 4.1.4.(b). Experimentally it is found that frictional force is proportional to normal force, i.e., \(f \propto N \) as shown in Figure 4.1.4.(c).
\begin{equation}
\text{or,} \quad f = \mu N\tag{4.1.2}
\end{equation}
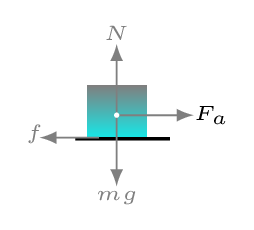

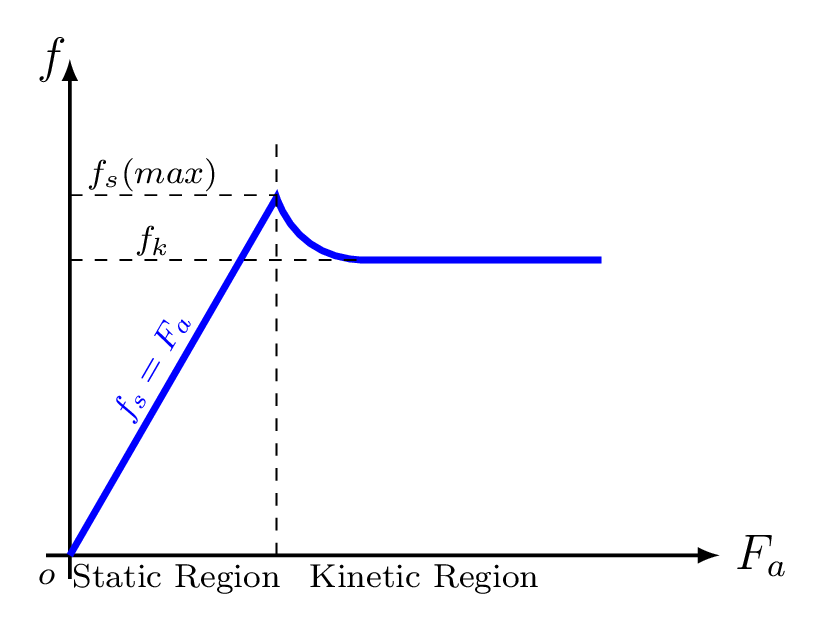
Where proportionality constant \(\mu\) is called coefficient of friction. It defines the nature of roughness of the surfaces being in contact. It is a dimensional less quantity. The coefficient of friction is a property of materials and does not change with the angle. For static friction, \(f_{s} \leq \mu_{s}\) N. The symbol \(\leq\) implies that static friction can have a maximum value of \(\mu_{s} N\text{.}\) Static friction is a responsive force that increases to be equal and opposite to whatever force is being exerted, up to its maximum limit. Once the applied force exceeds \(f_{s} (max) \text{,}\) the object moves. Thus, \(f_{s}(max) = \mu_{s} N\text{.}\) For kinetic friction, \(f_{k} =\mu_{k} N\text{.}\) Remember the direction of friction is always opposite to the direction of motion or applied force, not in the direction of normal. Hence the above equations has no vector form.
Friction decreases with increase in smoothness of the surfaces of contact as \(\mu\) decreases, but if the surfaces are ultra smooth then friction increases because of inter molecular forces starts to act between the two surfaces as they come very close to each other, due to which it becomes harder to make them slide on each other. Friction is a complex force, and its behavior is still not completely understood. On molecular level friction has no existence. In microscopic level most surfaces look very rough as shown in Figure 4.1.4.(b). Thus, when an object is pushed to move it must raise the object until it can skip the tips of the surface hitting, breaking off the points, or both. A considerable force can be resisted by friction with no apparent motion. Part of the friction is due to adhesive forces between he surface molecules of the two objects, which explains the dependence of friction on the nature of the substances. For example, rubber-soled shoes slip less than those with leather soles. Adhesion varies with substances in contact. Once an object is moving, there are fewer points of contact so less force is required to keep the object moving. At small but nonzero speeds, friction is nearly independent of speed.
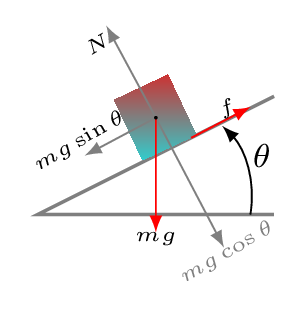
When an object is placed on the surface of an inclined plane and the angle of inclination is being increased slowly then at a particular angle the object just begins to slide, this angle is known an angle of repose, \(\phi\). At the angle of repose static frictional force is balanced by one of the components of weight \((mg\sin\theta)\) of the object (see in section statics).
\begin{align*}
mg\sin\theta \amp = f_{s}\\
and \qquad N \amp =mg\cos\theta
\end{align*}
\begin{equation*}
\therefore \quad \tan\theta = \frac{f_{s}}{N} = \frac{\mu_{s}N}{N}=\mu_{s}
\end{equation*}
\begin{equation*}
\theta_{repose}=\phi=\tan^{-1}(\mu_{s})
\end{equation*}
Force of Gravity: This force is acting on any object due to attraction of earth. Near the surface of the earth force of gravity is given by its weight, i.e., \(F_{g}=w=mg\text{.}\) Where \(g\) is the acceleration due to gravity and the direction force is acting along the center of the earth. Normal: This is a force of reaction from the surface where the object is placed. It is always perpendicular to the surface of contact. Tension: This force is acting between two objects on opposite ends of the string, in the directions to taut string at the points of contact. This force stretches the string along fixed support. It is a pulling force. Spring force: A spring is a special medium that has ability to restore its shape, if deformed. All materials have elastic property which helps them to restore their shape, if an applied deforming force has been released. From Hook’s law a material (spring) exerts a restoring force that is proportional to a deforming force in opposite direction in which it is stretched or compressed. In mathematical form,
\begin{equation}
\vec{F} = -k\vec{x}.\tag{4.1.3}
\end{equation}
The proportionality constant \(k\) is a measure of the spring’s stiffness, also called an elastic constant. The line of action of this force is parallel to the spring axis, and acts along the opposite direction of the displacement vector. The displacement must be measured from the relaxed (equilibrium) position; \(x = 0\) when the spring is relaxed.
