Subsection 2.1.2 Product of Two Vectors:
There are two ways in which vectors can be multiplied. The product of one of them is a scalar quantity, called a scalar product (or a dot product) and the other is a vector quantity, called a vector product (or a cross product).
Subsubsection 2.1.2.1 Scalar (or Dot) Product
The scalar product of two vectors \(\vec{a}\) and \(\vec{b}\) is denoted by \(\vec{a}\cdot \vec{b}\text{,}\) and is defined as
\begin{equation*}
\vec{a}\cdot {\vec{b}} = |\vec{a}| |\vec{b}| \cos\theta = ab\cos\theta,
\end{equation*}
where \(\theta\) is the angle between \(\vec{a}\) and \(\vec{b}\text{.}\)
Geometrical Interpretation:.
\begin{equation*}
\vec{a}\cdot {\vec{b}} = \vec{OA}\cdot {\vec{OB}} = (OA)(OB) \cos\theta = (OA)(ON)
\end{equation*}
= (length of \(\vec{a}\)) (projection of \(\vec{b}\) along \(\vec{a}\)).
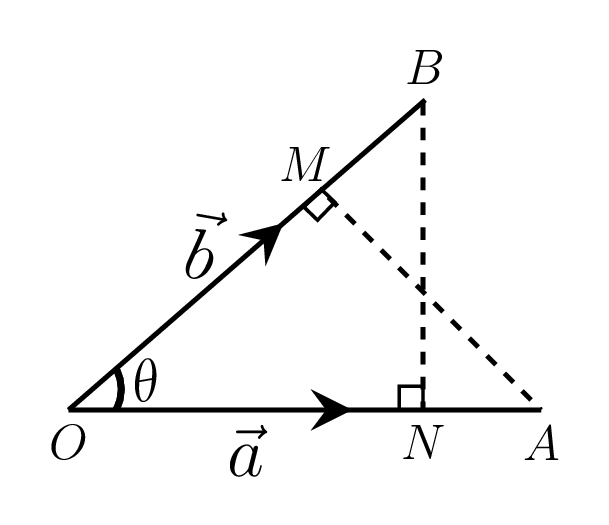
Therefore the dot product of two vectors is the product of length of one of these vectors and the projection of the other in the direction of the first.
Mnemonics:
\begin{equation*}
\hat{i}\cdot\hat{j}= \hat{j}\cdot\hat{k} = \hat{k}\cdot\hat{i} = 0
\end{equation*}
or,
\begin{equation*}
\hat{i}\cdot\hat{i} =\hat{j}\cdot\hat{j} = \hat{k}\cdot\hat{k} =1
\end{equation*}
Properties:
- Commutative law: \(\quad \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}\)
- Distributive law: \(\quad \vec{a} \cdot \left(\vec{b}+\vec{c} \right) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}\)
Subsubsection 2.1.2.2 Vector (or Cross) Product
The vector product of two vectors \(\vec{a}\) and \(\vec{b}\) is denoted by \(\vec{a}\times\vec{b}\) and is defined as
\begin{equation*}
\vec{a} \times \vec{b} = \mid{\vec{a}}\mid \mid{\vec{b}}\mid sin\theta \hat {n} = absin\theta {\hat{n}},
\end{equation*}
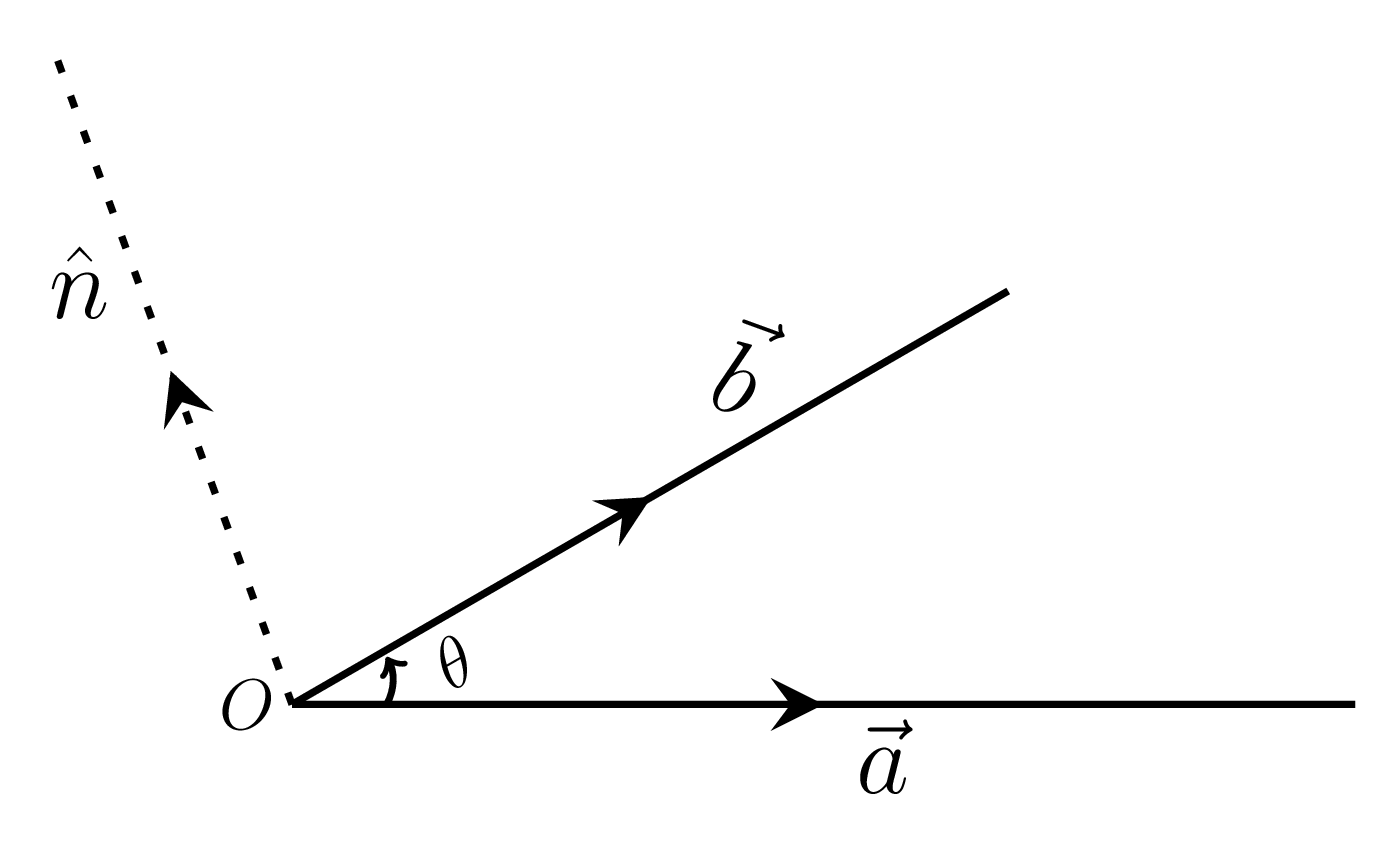
where \(\theta\) is the angle between \(\vec{a}\) and \(\vec{b}\text{,}\) and \({\hat{n}}\) is a unit vector perpendicular to the plane made by vectors \(\vec{a}\) and \(\vec{b}\text{,}\) and is representing the direction of \(\vec{a}\times\vec{b}\text{.}\) Here \(\vec{a}\text{,}\) \(\vec{b}\text{,}\) and \({\hat{n}}\) form a right handed system, as shown in Figure 2.1.4.(a).
Geometrical Interpretation:.
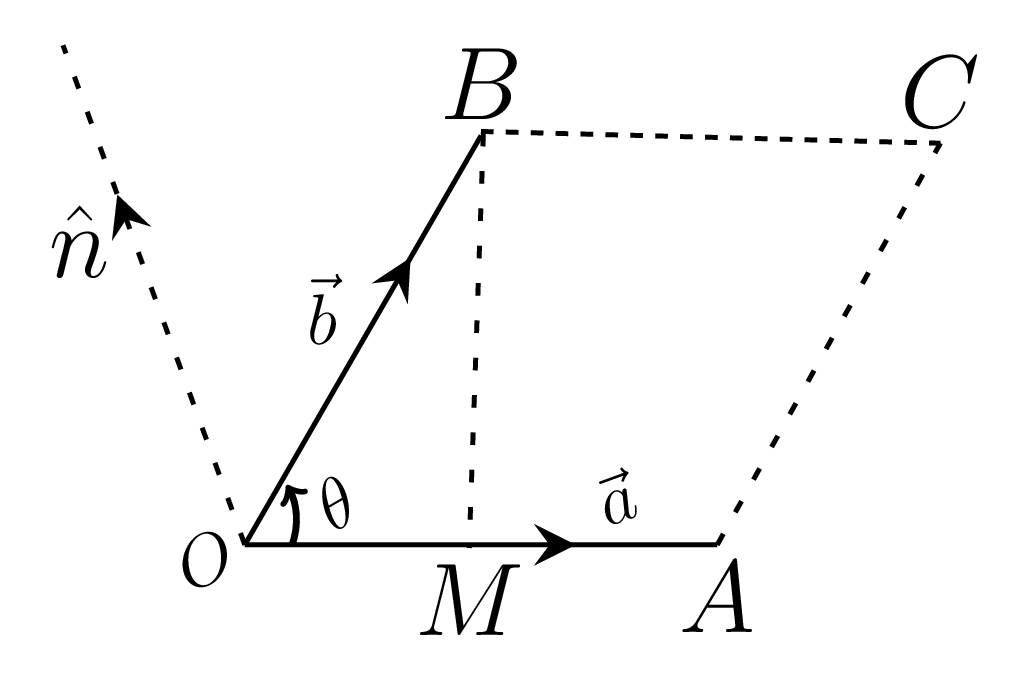
Let \(\vec{a}\) and \(\vec{b}\) be the adjacent sides of the parallelogram, as shown in Figure 2.1.4.(b), then
\begin{equation*}
\vec{a}\times\vec{b} = \vec{OA}\times\vec{OB} = (OA)(OB) \sin\theta \hat{n} = \left(OA\cdot{BM}\right){\hat{n}} = base \cdot height \quad \hat{n}
\end{equation*}
= vector area of parallelogram OACB.
i.e., a vector product of two vectors is the vector area of a parallelogram constructed by these vectors.
Vector product in determinant form.
If \(\vec{a} = a_{1}\hat{i}+a_{2}\hat{j}+ a_{3}\hat{k}\) and \(\vec{b} = b_{1}\hat{i}+b_{2}\hat{j}+ b_{3}\hat{k}\) then
\begin{equation*}
\vec{a}\times\vec{b} =\left( {a_{1}\hat{i}+a_{2}\hat{j}+ a_{3}\hat{k}}\right)\times \left( {b_{1}\hat{i}+b_{2}\hat{j}+ b_{3}\hat{k}}\right)
\end{equation*}
\begin{equation*}
=(a_{2}b_{3}-a_{3}b_{2})\hat{i}- (a_{1}b_{3}-a_{3}b_{1})\hat{j} + (a_{1}b_{2}-a_{2}b_{1})\hat{k}
\end{equation*}
\begin{equation*}
=\begin{bmatrix} \hat{i} & \hat{j} & \hat{k} \\a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{bmatrix}
\end{equation*}
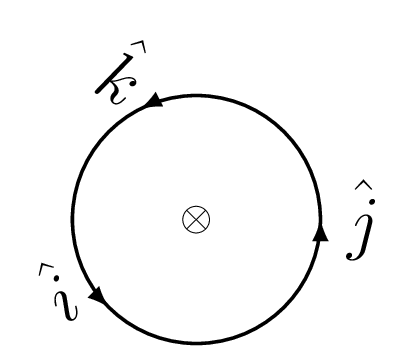
Mnemonics:.
\begin{equation*}
\hat{i}\times\hat{j}=\hat{k};\qquad \hat{j}\times\hat{k}=\hat{i};\qquad \hat{k}\times\hat{i}=\hat{j}
\end{equation*}
or,
\begin{equation*}
\hat{i}\times\hat{k}=-\hat{j};\qquad \hat{k}\times\hat{j}=-\hat{i};\qquad \hat{j}\times\hat{i}=-\hat{k}
\end{equation*}
Properties:.
- Commutative Law: \(\quad \vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)
- Distributive law: \(\quad \vec{a} \times \left(\vec{b}+\vec{c} \right) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\)
