Section 8.1 Hooke’s Law
Hook’s law states that within the elastic limit, stress is proportional to strain. Stress, \(\sigma\text{:}\) It is an internal pressure exerted by the material. It is equal and opposite to the applied pressure. Stress is defined as a force per unit cross-sectional area.
\begin{equation*}
\sigma = F/A.
\end{equation*}
Strain, \(\epsilon\text{:}\) It is a change in dimension of the material per unit original dimension.
\begin{equation*}
\epsilon = \Delta L/L
\end{equation*}
\begin{equation*}
\text{or,}\quad\epsilon= \Delta \theta/\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad\epsilon=\Delta V/V
\end{equation*}
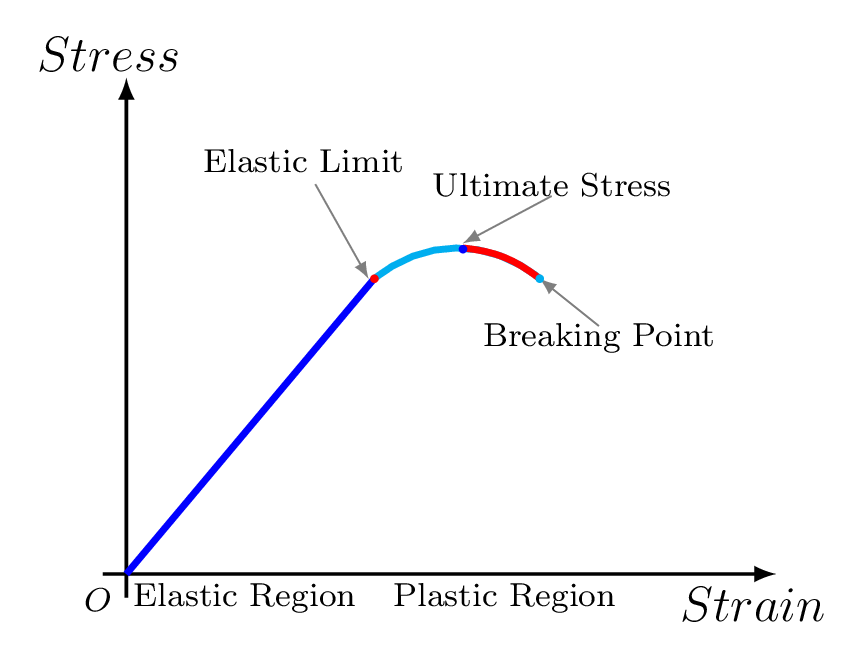
If the deforming force is applied on a material, initially strain increases gradually and remains proportional to the stress for a certain limit. After this high stress the atoms are pulled permanently away from their equilibrium position in the lattice structure. The maximum stress which the wire can experience and still return to its original length is called the elastic limit and the region is called elastic region as shown in Figure 8.1.1. Hooke’s law holds good only within this limit. If the stress is increased beyond this limit, the ultimate stress point is reached which is the highest point on the stress-strain curve. This is the greatest stress that the material can bear. Brittle materials break suddenly at this point, while some ductile materials can be stretched a little more due to a decrease in the cross-sectional area of the material. But they too break shortly thereafter at the breaking point. This region is called a plastic region.
