Subsection 6.1.1 Acceleration Due to Gravity, \(g\)
From Newton’s II law of motion, when an external unbalanced force acts on an object, it will give an acceleration \(a\) to that object, that is, \(F = ma\text{.}\) But, if the gravitational force is acting on the body near the surface of the earth, then the body experiences the acceleration \(g\) for a freely falling body. This force is called weight of the body, \(w = mg\text{.}\) Hence,
\begin{equation*}
F=mg=G\frac{Mm}{R^{2}} \quad \Rightarrow\quad g=\frac{GM}{R^{2}}
\end{equation*}
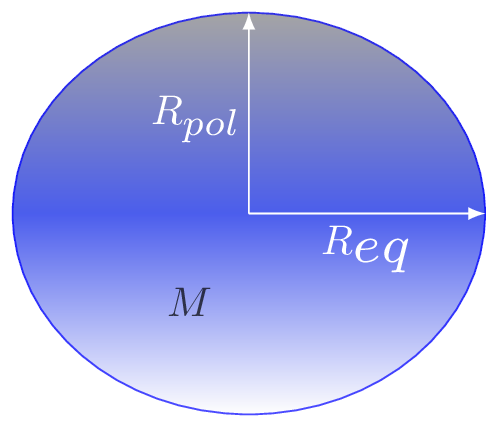
Where \(M, \quad m,\) and \(R\) are the mass of earth, mass of a body on the surface of the earth, and the radius of the earth, respectively. The shape of earth is not a perfect sphere, rather, it is an oblate spheroid. That is, the radius of the earth at the equator \(R_{eq}\) is slightly greater than the radius of the earth at the poles \(R_{pol}\) as shown in Figure 6.1.1. Hence the value of \(g\) varies slightly with latitude on the surface of the earth as \(g \varpropto \frac{1}{R^{2}},\) since G and M are constants. The value of
\begin{equation*}
R_{pol}=6.356\times10^{6}m, \quad R_{eq} = 6.378\times10^{6}m,
\end{equation*}
The mean value of \(R = 6.371\times10^{6}m.\) Even though the variation in the radius of the earth seems quite small, the variation in the acceleration due to gravity on the earth goes from as low as \(9.78 m/s^{2}\) at the equator to as high as \(9.83 m/s^{2}\) at the north Pole.
Subsubsection 6.1.1.1 Effect of the Rotation of the Earth on g
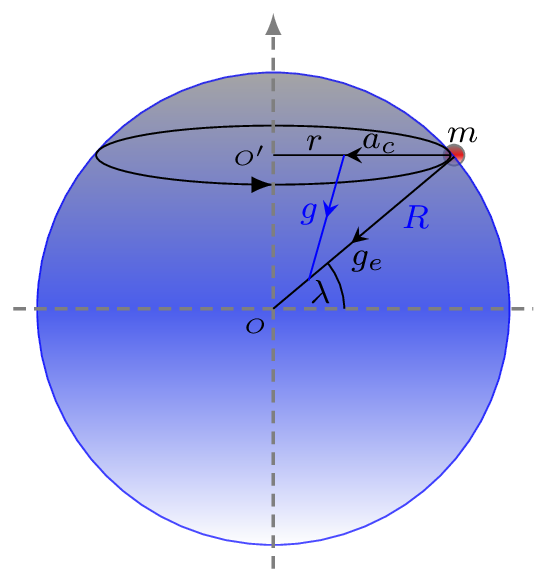
The value of \(g\) on the surface of the earth does not only vary with the radius of the earth but it is also affected by the rotation of the earth. Any mass rotating in a circular motion needs a centripetal force which is acting towards the center of the circular path. Remember that a centripetal force is not a real force that is acting on a rotating body, but it is the required force that must be applied to keep the body in that rotational motion. Hence the part of gravitational force must be acting on a body to provide a necessary centripetal force to keep that object moving on a circle with the rotation of the earth as shown in Figure 6.1.3.
Since the centripetal force \(\vec{F}_{c}=m\vec{a}_{c}\) required by the mass m to follow a circle of radius r, then this force must be provided by the vector difference in force of gravity \(\vec{F_{e}}=m\vec{g}_{e} \) and a real force \(F=m\vec{g}\text{,}\) i.e.,
\begin{equation*}
\vec{F}_{c}=\vec{F_{e}}-\vec{F}
\end{equation*}
\begin{equation*}
\text{or,}\quad m\vec{a}_{c} = m\vec{g}_{e}-m\vec{g}
\end{equation*}
\begin{equation*}
\therefore \vec{g}=\vec{g}_{e}-\vec{a}_{c}
\end{equation*}
The magnitude of \(\vec{g}\) can be found by
\begin{equation*}
\vec{g}\cdot\vec{g} =g^{2}= \left(\vec{g}_{e}-\vec{a}_{c}\right) \cdot\left(\vec{g}_{e}-\vec{a}_{c}\right)
\end{equation*}
\begin{equation*}
= \vec{g}_{e}\cdot\vec{g}_{e} + \vec{a}_{c}\cdot\vec{a}_{c}-2\vec{g}_{e}\cdot\vec{a}_{c} =g^{2}_{e}+a^{2}_{c}-2g_{e}a_{c}\cos\lambda
\end{equation*}
\begin{equation*}
\therefore g= \sqrt{g^{2}_{e}+a^{2}_{c}-2g_{e}a_{c}\cos\lambda}
\end{equation*}
where
\begin{equation*}
a_{c}=r\omega^{2} = R\omega^{2}\cos\lambda,
\end{equation*}
R is the radius of the earth, and the acceleration due to gravity on a non-rotating earth is
\begin{equation*}
g_{e}= \frac{GM}{R^{2}}.
\end{equation*}
Subsubsection 6.1.1.2 Effect of Altitude of the Earth on g
Acceleration due to gravity on the surface of the earth is given by
\begin{equation*}
g=\frac{GM}{R^{2}}
\end{equation*}
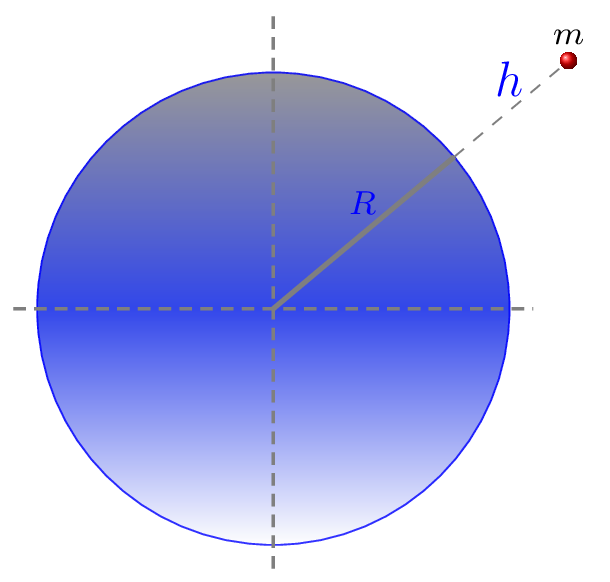
At height \(h\) from the surface of the earth [Figure Figure 6.1.4], acceleration due to gravity is given by
\begin{equation*}
g_{h} = \frac{GM}{(R+h)^{2}} = \frac{GM}{R^{2}\left(1+\frac{h}{R}\right)^{2}}
\end{equation*}
\begin{equation*}
=\frac{g}{\left(1+\frac{h}{R}\right)^{2}}=g\left(1+\frac{h}{R}\right)^{-2} =g\left(1-\frac{2h}{R} +\cdots\right)
\end{equation*}
using binomial theorem
\begin{equation*}
\therefore \quad g_{h} =g\left(1-\frac{2h}{R}\right)
\end{equation*}
Subsubsection 6.1.1.3 Effect of Depth of the Earth on g
Acceleration due to gravity on the surface of the earth is given by
\begin{equation*}
g=\frac{GM}{R^{2}}= \frac{G}{R^{2}}\left(\frac{4}{3}\pi R^{3}\rho\right) = \frac{4}{3}G\pi R\rho
\end{equation*}
where mass of the entire earth,
\begin{equation*}
M=Volume\times density = \left(\frac{4}{3}\pi R^{3}\right)\times \rho
\end{equation*}
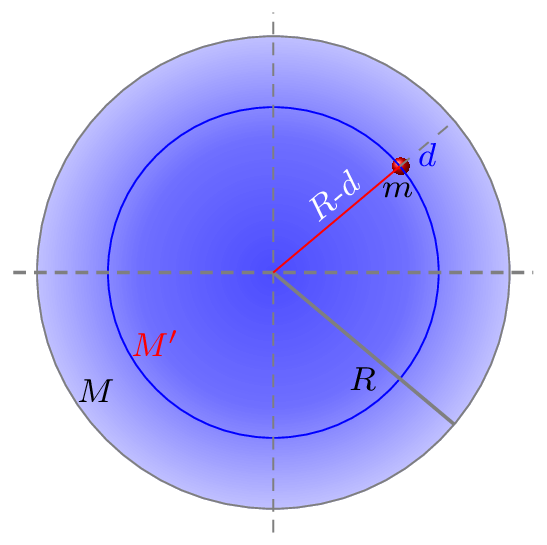
At depth \(d\) from the surface of the earth, mass of the earth
\begin{equation*}
M'=\frac{4}{3}\pi (R-d)^{3} \rho
\end{equation*}
[Figure 6.1.5]. Therefore the acceleration due to gravity at that depth is given by
\begin{equation*}
g_{d} = \frac{GM'}{(R-d)^{2}} = \frac{\frac{4}{3}G\pi (R-d)^{3} \rho}{(R-d)^{2}}
\end{equation*}
\begin{equation*}
=\frac{4}{3}G\pi (R-d) \rho = \frac{4}{3}G\pi \rho R\left(1-\frac{d}{R}\right)
\end{equation*}
\begin{equation*}
\therefore \quad g_{h} =g\left(1-\frac{d}{R}\right)
\end{equation*}
