Subsection 10.3.8 Solar Constant
It is the rate at which solar energy received by the unit surface area of the earth, when it is placed at the mean sun-earth distance. Solar constant, \(S = 1353 \,W/m^{2}.\)
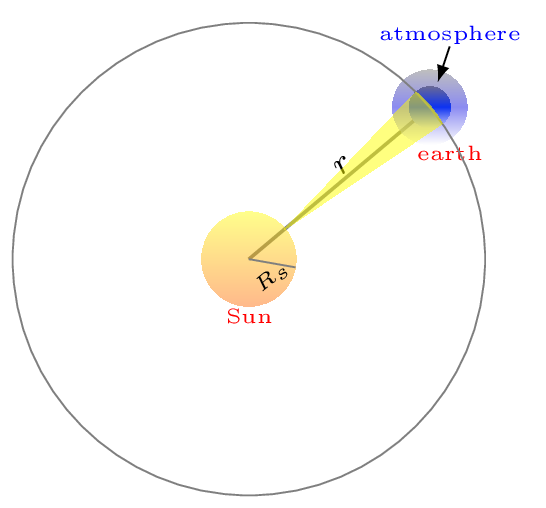
If \(R_{s}\) be the radius of the sun and \(T\) be its surface temperature, then by considering the sun as a perfect black body, solar energy radiated by the sun surface is given by
\begin{equation*}
P=\sigma \left(4\pi R_{s}^{2}\right) T^{4}
\end{equation*}
If \(r=1.496\times10^{11} \,m\) be the mean sun-earth distance then sun’s energy is radiated in the spherical surface of area \(4\pi r^{2} \text{.}\) Hence the energy received by unit surface on the earth is
\begin{equation*}
S=\frac{P}{ 4\pi r^{2}}
\end{equation*}
\begin{equation*}
= \frac{\sigma \left(4\pi R_{s}^{2}\right) T^{4}}{4\pi r^{2}} = \sigma T^{4}\left(\frac{R_{s}}{r}\right)^{2}
\end{equation*}
\begin{equation*}
\text{or,}\quad T^{4}=\frac{S}{\sigma}\left(\frac{r}{R_{s}}\right)^{2}
\end{equation*}
\begin{equation*}
\therefore\quad T =\sqrt[4]{\frac{S}{\sigma}\left(\frac{r}{R_{s}}\right)^{2}}
\end{equation*}
\begin{equation*}
=\sqrt[4]{\frac{1353(W/m^{2})}{5.67\times 10^{-8}(W/m^{2})}\left(\frac{1.496\times 10^{11}\,m}{6.98\times10^{8}\,m}\right)^{2}}
\end{equation*}
\begin{equation*}
=5762 \,K
\end{equation*}
