Example 4.2.1.
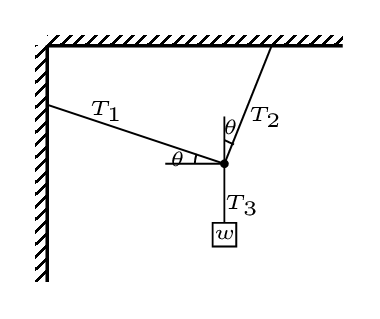
What is the tension in each of the strings of the system shown here:
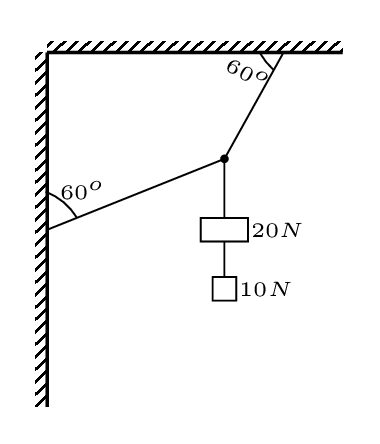
Solution.
Step 1. List the given quantities and label the diagram:
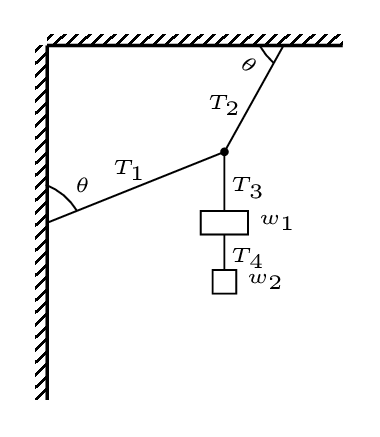
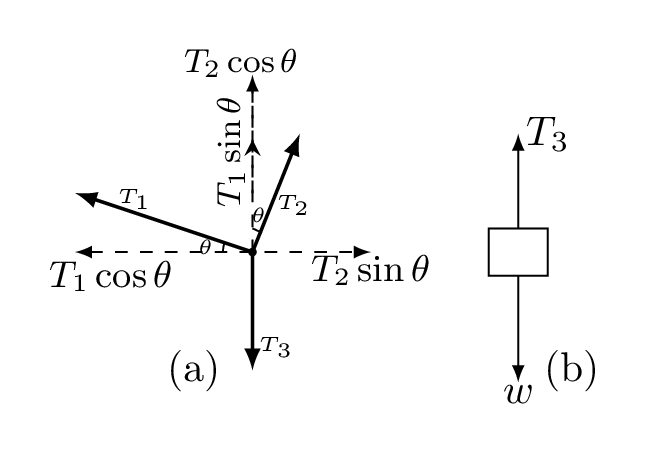
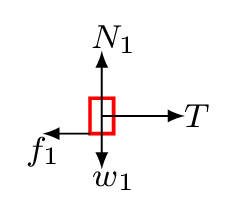
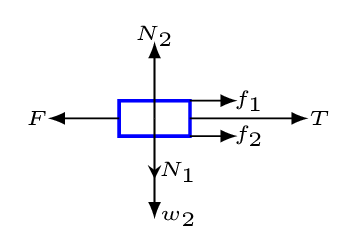
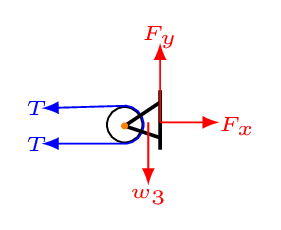
Step 2. Isolate each object and draw the force diagrams:
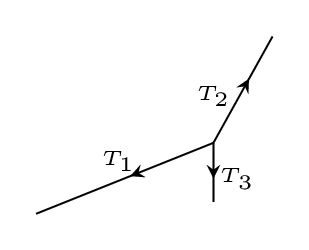
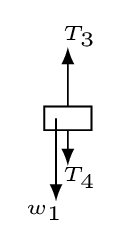
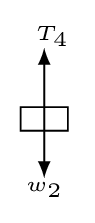



Step 3. Resolve forces into components as shown in figure:
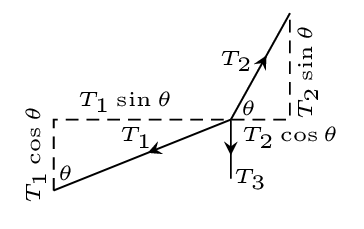
Step 4. Write equations using the figure

\begin{equation*}
\sum{F_{x}} = T_{2}\cos\theta - T_{1}\sin\theta = 0
\end{equation*}
\begin{equation*}
\sum{F_{y}} = T_{2}\sin\theta - T_{1}\cos\theta -T_{3}= 0
\end{equation*}
from figure 

\begin{equation*}
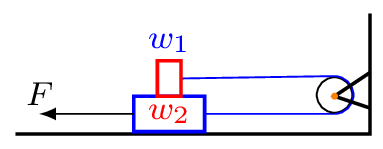
\sum{F_{y}} = T_{3}-w_{1}-T_{4}= 0
\end{equation*}
from figure 

\begin{equation*}
\sum{F_{y}} = T_{4}-w_{2} = 0
\end{equation*}
Step 5. Solve equations simultaneously for unknowns:
\begin{equation*}
T_{4} = w_{2} = 10 \,N
\end{equation*}
\begin{equation*}
T_{3} = T_{4} + w_{1} = 30 \,N
\end{equation*}
\begin{equation*}
Now,\quad T_{2} = \frac{T_{1}\sin\theta}{\cos\theta}= T_{1}\tan\theta
\end{equation*}
\begin{equation*}
also,\quad T_{1} = \frac{T_{3}}{\tan\theta\sin\theta-\cos\theta} = 30 \,N;
\end{equation*}
\begin{equation*}
\therefore T_{2} =52 \,N
\end{equation*}