General Physics I:

A body which does not deform (i.e., the distance between two points never changes) under the influence of forces is known as a rigid body. However, there is no such thing as a perfect rigid body in real life. Practically all bodies deform somewhat more or less with the applied force. A rigid body conserves its shape under the action of external forces. A concrete pillar, a dead snake, bones, etc can be considered as rigid bodies. In rigid body a physics of real object is described for its real dimension not as we have described physics earlier for an object by considering it as a point mass.

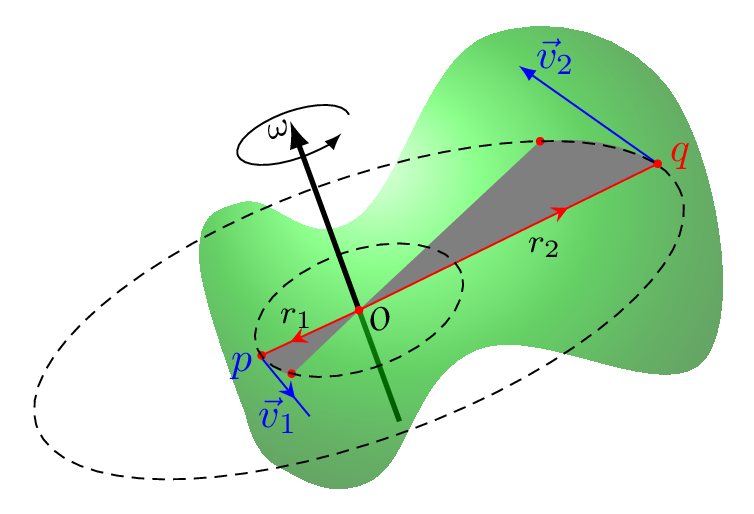
The movement of a rigid body not fixed to an axis shows a translation motion while a body with fixed axis shows a combination of translational and rotational motion. In translational motion all the particles of a system have same velocity and acceleration as the velocity and acceleration of its center of mass. In rotational motion different particles of a body moves in different circular paths with all their centers lie on a point of rotation. The straight line that is passing through the point of rotation and perpendicular to the plane of circular paths is called an axis of rotation. In rotational motion every particle of the system follows the same angular velocity but has different tangential velocities which depends upon their position from the axis of rotation. The further the particle from the axis of rotation, the higher will be their tangential velocities. The angular measurements is described in radian rather than degree in the rigid body. In Figure 7.0.1, angular velocity, \(\omega\) is pointed along the axis of rotation which is given by the right hand thumb’s rule, where if fingers of right hand are curled in the direction of rotation then thumb is directed along the angular velocity. Point \(O\) is a point of rotation and the tangential velocities of particles \(p\) and \(q\) are given as \(\vec{v}_{1}\) and \(\vec{v}_{2},\) respectively where magnitude of \(\vec{v}_{2} \gt \vec{v}_{1}.\)