Subsection 3.1.3 Relative velocity
It is the velocity that an object \(A\) would appear (to be moving or at rest) to an observer on the object \(B\) and vice-versa. If \(v_{AB}\) is a velocity vector of an object \(A\) relative to another object \(B\text{,}\) then
\begin{equation*}
\vec{v}_{AB} = - \vec{v}_{BA}
\end{equation*}
and the basic equation for relative velocity becomes:
\begin{equation*}
\vec{v}_{az} = \vec{v}_{ab} + \vec{v}_{bc} + \cdots + \vec{v}_{yz}
\end{equation*}
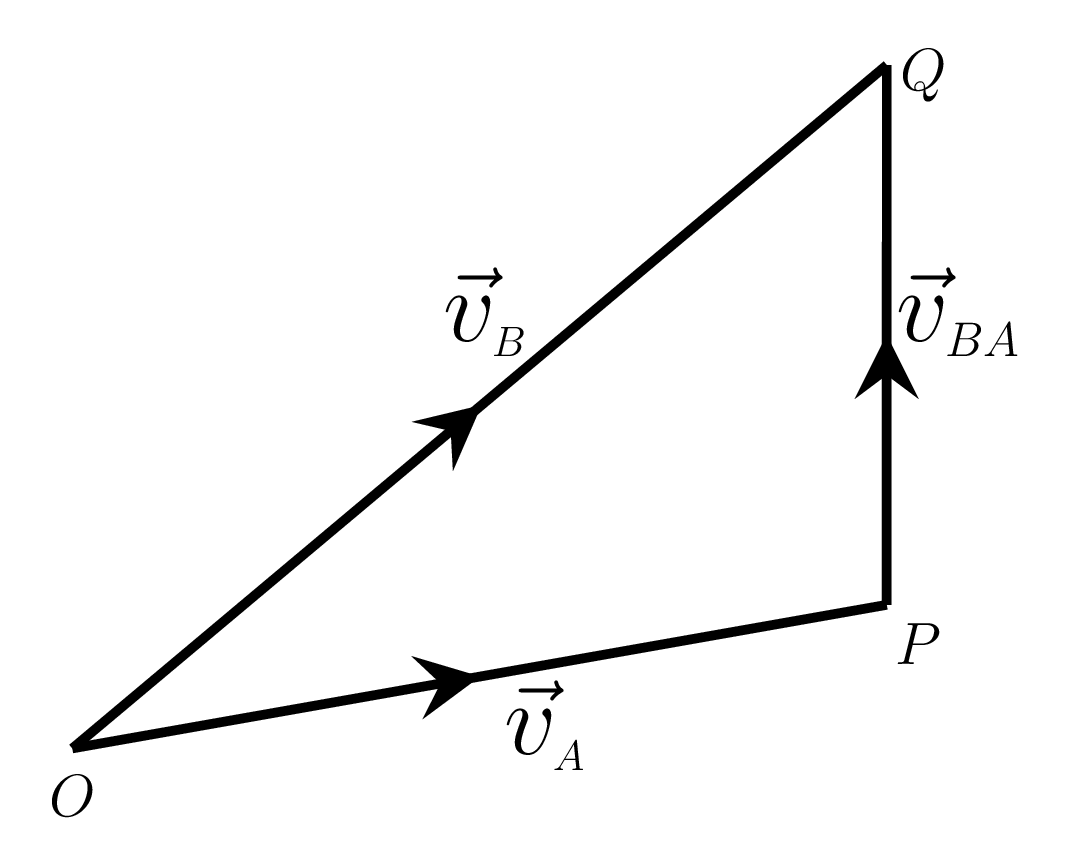
From Figure 3.1.9.(a) we have
\begin{equation*}
\vec{v}_{A}+\vec{v}_{BA} = \vec{v}_{B}
\end{equation*}
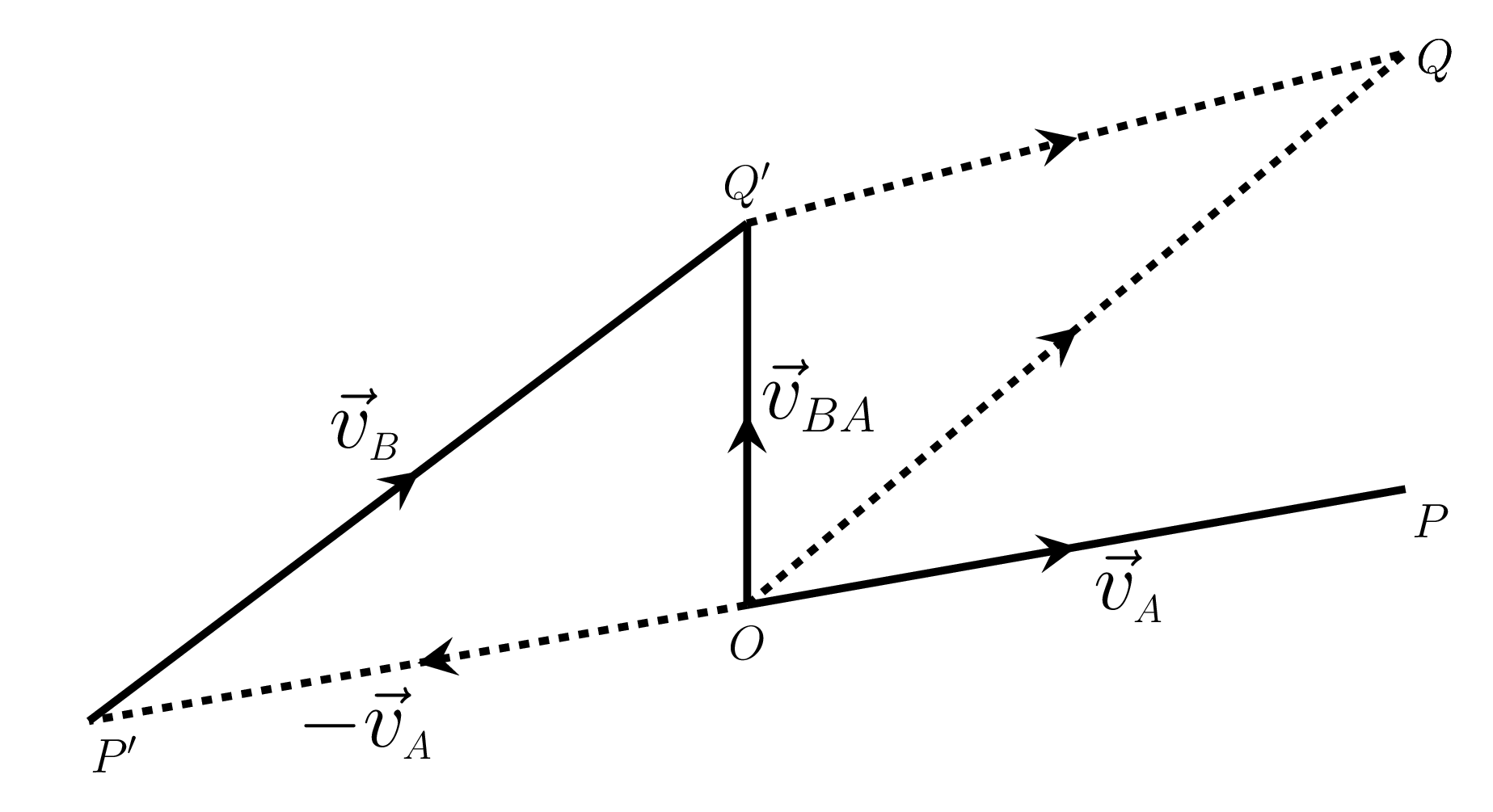
and from Figure 3.1.9.(b),
\begin{equation*}
-\vec{v}_{A}+\vec{v}_{B} = \vec{v}_{BA};
\end{equation*}
\begin{equation*}
\therefore \vec{v}_{BA} =\vec{v}_{B}-\vec{v}_{A}
\end{equation*}
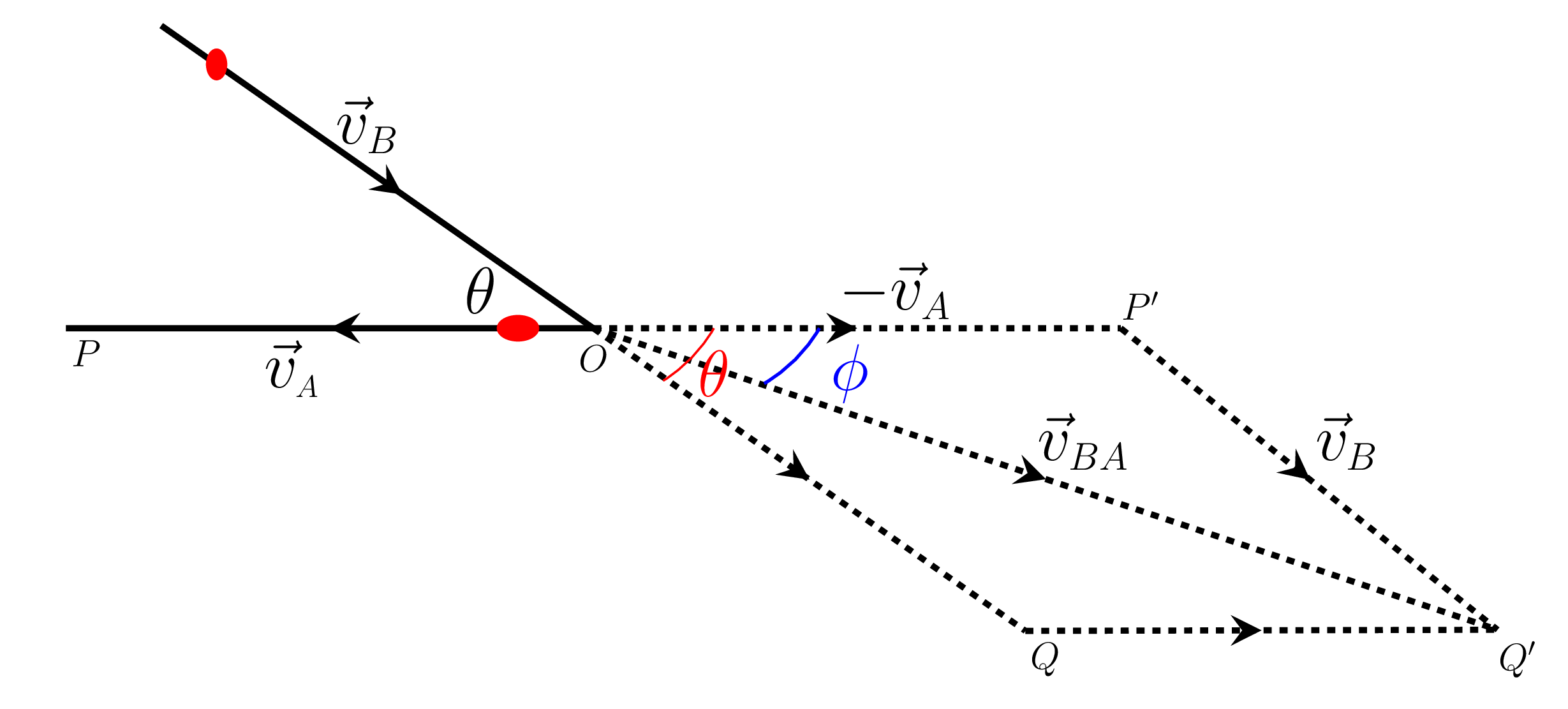
where \(\vec{v}_{A} \) and \(\vec{v}_{B}\) are called absolute velocities of objects A and B, respectively. Consider an airplane \(A\) is coming with velocity \(\vec{v}_{A} =600 \quad km/h\) due \(\theta=35^{o}\) south of east and another one \(B\) is coming with velocity \(\vec{v}_{A} =700 \quad km/h\) due west as shown in Figure 3.1.9.(c). Find the relative velocity of \(B\) with respect to \(A\text{.}\) To solve such problem assume that object \(A\) is at rest. The object \(A\) must be the object with respect to which we are finding the velocity of object \(B\text{.}\)
To assume that the object \(A\) is at rest take its velocity in negative direction to draw a parallelogram of adjacent vectors \(\vec{v}_{B}\) and \(-\vec{v}_{A}\) so that their resultant velocity is \(\vec{v}_{BA} \text{.}\) From Figure 3.1.9.(c), we have -
\begin{equation*}
\vec{v}_{BA} = -\vec{v}_{A}+\vec{v}_{B};
\end{equation*}
\begin{equation*}
v_{Bx}=v_{B}\cos\theta = 491.5 \quad km/h,
\end{equation*}
\begin{equation*}
v_{By}=v_{B}\sin\theta = 344 \quad km/h,
\end{equation*}
\begin{equation*}
\text{and} v_{A}=700 \quad km/h
\end{equation*}
\begin{equation*}
v_{Rx}=v_{A}+v_{Bx}=1191.5 \quad km/h;
\end{equation*}
\begin{equation*}
v_{Ry}=v_{By}=344 \quad km/h
\end{equation*}
\begin{equation*}
\therefore v_{BA} = \sqrt{v^{2}_{Rx}+ v^{2}_{Ry}} = 1240.16 km/h
\end{equation*}
where the direction of relative velocity is given by
\begin{equation*}
\phi = \tan^{-1}\left(\frac{v_{Ry}}{v_{Rx}}\right) = 16^{o} \quad \text{S of E}.
\end{equation*}
