Subsection 4.5.1 Atwood’s Machine
It is device where two masses \(m_{1}\) and \(m_{2}\) are hung at both ends of a massless, unstretchable string that runs over a frictionless and massless pulley as shown in figure below. This machine is used to learn the concept of dynamics in a little complex condition. In massless and frictionless pulley tension on both sides of the string and the magnitude of acceleration of both masses remain the same as there is no slack in the string as it moves.
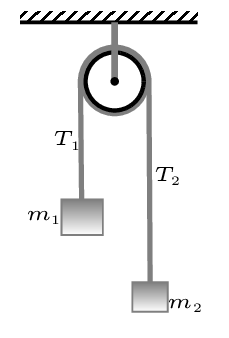
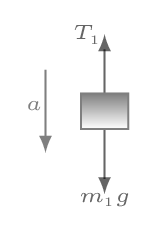
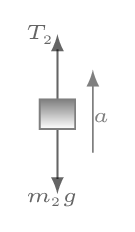
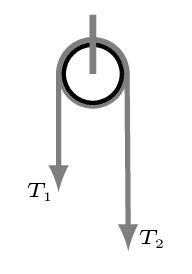
From free body diagram Figure 4.5.1.(b), we have -
\begin{equation}
m_{1}g-T_{1} =m_{1}a \quad \Rightarrow \quad T_{1} = m_{1}g-m_{1}a \tag{4.5.1}
\end{equation}
From free body diagram Figure 4.5.1.(c), we have -
\begin{equation}
T_{2}-m_{2}g- =m_{2}a \quad \Rightarrow \quad T_{2} = m_{2}g+m_{2}a \tag{4.5.2}
\end{equation}
System as a whole from figure Figure 4.5.1.(a), we have -
\begin{equation*}
F_{net} = (m_{1}+m_{2})a
\end{equation*}
\begin{equation}
\text{or,}\quad m_{1}g-m_{2}g = (m_{1}+m_{2})a\quad \Rightarrow \quad a=\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})} \tag{4.5.3}
\end{equation}
Therefore from eqn. (4.5.1), we get -
\begin{equation}
T_{1} = m_{1}g-m_{1}\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}= \frac{2m_{1}m_{2}g}{(m_{1}+m_{2})} \tag{4.5.4}
\end{equation}
Also from eqn.(4.5.2), we get -
\begin{equation}
T_{2} = m_{2}g+m_{2}\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}= \frac{2m_{1}m_{2}g}{(m_{1}+m_{2})}\tag{4.5.5}
\end{equation}
Hence from eqns.(4.5.4) and (4.5.5), it is clear that \(T_{1}=T_{2}\) in massless and frictionless pulley. We can see in rigid body dynamics that when pulley has mass and friction, \(T_{1}\) is no longer equal to \(T_{2}\text{.}\) Now, we can evaluate velocity of masses as
\begin{equation*}
a=\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\,dv}{\,dt}=\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}
\end{equation*}
\begin{equation*}
\text{or,}\quad \,dv =\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}\,dt
\end{equation*}
\begin{equation*}
\text{or,}\quad \int\limits_{0}^{v(t)}\,dv =\int\limits_{0}^{t}\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}\,dt
\end{equation*}
\begin{equation*}
\therefore\quad v(t) =\frac{(m_{1}-m_{2})g}{(m_{1}+m_{2})}t
\end{equation*}
Also, the distance traveled in time \(t\) is given by -
\begin{equation*}
v(t)=\frac{\,dx}{\,dt} \quad \Rightarrow \int\limits_{0}^{x(t)}\,dx =\frac{(m_{1}-m_{2})}{(m_{1}+m_{2})}g\int\limits_{0}^{t}t\,dt
\end{equation*}
\begin{equation*}
\therefore\quad x(t) = \frac{(m_{1}-m_{2})}{(m_{1}+m_{2})}\left(\frac{gt^{2} }{2}\right)
\end{equation*}
