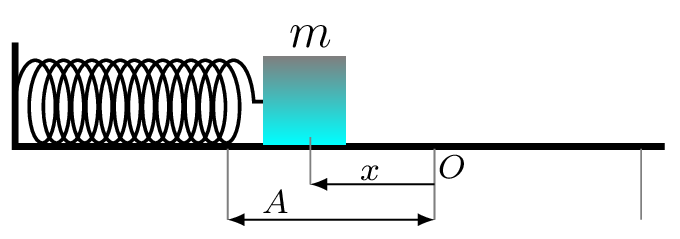
Example 7.6.1.
A mass of 1 kg resting on a frictionless horizontal surface is pressed against a spring of constant 100 N/m compressing the spring 25 cm and released from rest as shown in the figure below. 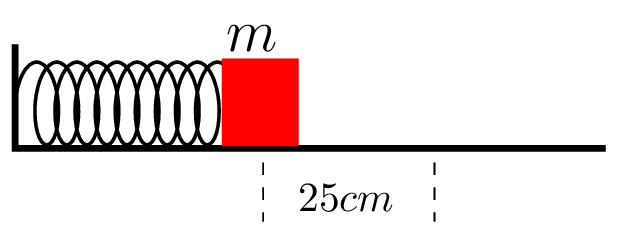

- Where will the block attain its fastest velocity?
- How fast will it be moving at that time?
- Where will it stop again?
- What will it do after it stops?
- Where does the block attain its greatest acceleration?
- What is that acceleration?
- Describe the motion of the block as time progresses.
- Write the equation of motion for the block.
- Write the equation for the velocity of the block.
- Write the equation for the acceleration of the block.
- Compare (h) with (j) to obtain a relationship between \(a\) and \(x\) for the block.
- Apply Newton’s Second Law to the block so as to find \(a\) in terms of \(x.\)
- Compare (k) with (l) to obtain a relationship between \(k\) and \(m\) at (\(x=A\)) for the block.
- How long does it take for the block to reach the equilibrium point the first time?
- How fast is the block moving when it is 10 cm beyond the equilibrium point?
- What is the energy of the block when it is 10 cm beyond the equilibrium point?
Solution.
Given: \(m = 1 \,kg, \quad k = 100 \,N/m,\quad A = 0.25 \,m,\quad v_{o} = 0,\) \(\omega = \sqrt{\frac{k}{m}}=10 \,rad/s. \)
- The velocity particle in shm is given by\begin{equation*} v=A\omega\sin\omega t. \end{equation*}For \(v\) to be maximum, \(\sin\omega t=1 \Rightarrow\omega t=\frac{\pi}{2}\text{.}\) Hence the position of the particle at that time is\begin{equation*} x=A\cos\omega t = A\cos\frac{\pi}{2}=0 \end{equation*}i.e., at the equilibrium position: \(x = 0.\)
-
At equilibrium position, velocity of the block is \(v=A\omega = 0.25\times10= 2.5 \,m/s.\)Alternatively: The total potential energy at extreme position is converted into total kinetic energy at mean position, i.e.,\begin{equation*} 1/2 k A^{2} = 1/2 m v^{2} \quad \Rightarrow \quad v = \omega A = 2.5 \,m/s \end{equation*}
- Velocity,\begin{equation*} v=A\omega\sin\omega t =0 \quad \Rightarrow \quad \omega t=0. \end{equation*}Therefore,\begin{equation*} x=A\cos\omega t = A. \end{equation*}Hence at 25 cm to the right of equilibrium: \(x = 0.25 \,m.\)
- Because of maximum restoring force it starts accelerate to the left.
- Since the restoring force is maximum at extremes, it attains maximum acceleration (\(a=-\omega^{2}x\)) at that points. Hence at the extremes, where it stops: \(x = A= \pm 0.25 \,m.\)
- \begin{equation*} k x = m a \Rightarrow a = \omega^{2}A = 25 \,m/s^{2} \end{equation*}
- It speeds up, coasts through equilibrium, slows down, stops, and reverses itself.
- \begin{equation*} x = - A \cos\omega t, \quad \omega = \Rightarrow x = - (0.25 \,m) \cos((10 \,rad/s) t) \end{equation*}
- \begin{equation*} v = dx/dt = \omega A \sin\omega t \Rightarrow v = (2.5 \,m/s) \sin ((10 \,rad/s) t) \end{equation*}
- \begin{equation*} a = \,d^{2}x/\,dt^{2} = \omega^{2} A \cos\omega t \Rightarrow a = (25 \,m/s^{2}) \cos ((10 \,rad/s) t) \end{equation*}
- \begin{equation*} \frac{a}{x} = -100 = -\omega^{2} \quad \Rightarrow a=-\omega^{2} x \end{equation*}
- \begin{equation*} - k x = m a \Rightarrow a = - \frac{k}{m} A \end{equation*}
- \begin{equation*} \frac{a}{a} = \frac{-\omega^{2} A}{- \frac{k}{m} A}\quad \Rightarrow\quad \omega^{2} = k/m \quad \Rightarrow \omega = \sqrt{\frac{k}{m}} \end{equation*}
- \begin{equation*} [x = - (0.25 m) \cos ((10 rad/s) t) = 0 \Rightarrow \cos 10t =\cos \frac{\pi}{2} \end{equation*}\begin{equation*} \quad \therefore t=\frac{\pi}{20} = 0.157 \,s \end{equation*}
- \begin{equation*} 1/2 k A^{2} = 1/2 m v^{2} + 1/2 k x^{2}, \quad \text{at}\quad x = 0.1 \,m, \end{equation*}\begin{equation*} v = \omega\sqrt{A^{2}-x^{2}}= 2.29 \,m/s \end{equation*}
- \begin{equation*} E = \frac{1}{2} k A^{2} = 3.125 \,J \end{equation*}