Subsection 7.3.4 The Gyroscope
It is a spinning disc or wheel in which the axis of rotation is free to orient in any direction. It is used to detect rotational movement. It is very useful in navigation, especially where magnetic compasses can’t be used, such as in spacecraft, intercontinental ballistic missiles, and satellites. Wheels on a bicycle, for example, act as gyroscopes as they spin up to speed, making it easier to stay upright and harder to upset momentum.
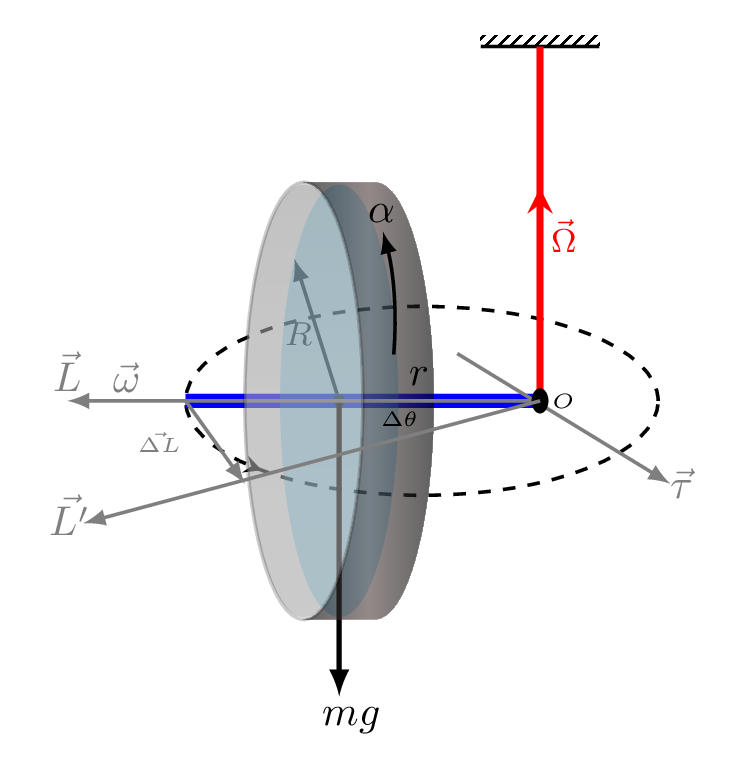
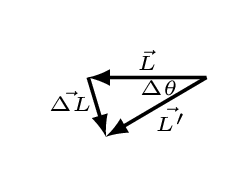
In the Figure 7.3.5, \(L\) and \(L'\) are initial and final angular momentum after time \(\Delta t,\) respectively. \(\omega\) is angular velocity of wheel rotation and \(\Omega\) is a precessional velocity. \(\vec{r}\) is the distance of wheel from the axis of rotation, \(O\text{.}\) \(\tau\) is the direction of torque being acted on the wheel because of its weight. The direction of torque can be given by right hand thumb rule. When the right hand fingers are curled from the direction along \(\hat{r}\) to the direction along weight then the direction of thumb will be pointed along the torque. Because of torque the direction of angular momentum changes every second hence the orientation of new angular momentum is given by
\begin{equation*}
\Delta L = L\Delta\theta
\end{equation*}
\begin{equation*}
\text{or,}\quad \frac{\Delta L }{\Delta t}= L\frac{\Delta\theta}{\Delta t}
\end{equation*}
\begin{equation*}
\tau = L\Omega
\end{equation*}
\begin{equation*}
\therefore \quad \Omega = \frac{\tau}{L} = \frac{mgr}{I\omega}
\end{equation*}
Earth precesses because of the torque produced on it due to gravitational tidal force of the Sun and the Moon.
