Skip to main content Contents Index Prev Up Next \(\newcommand{\N}{\mathbb N}
\newcommand{\Z}{\mathbb Z}
\newcommand{\Q}{\mathbb Q}
\newcommand{\R}{\mathbb R}
\newcommand{\T}{\mathcal T}
\newcommand\comb[2]{^{#1}C{_{#2}}}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\definecolor{fillinmathshade}{gray}{0.9}
\newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}}
\)
Subsection 1.4.3 The Volume Integral
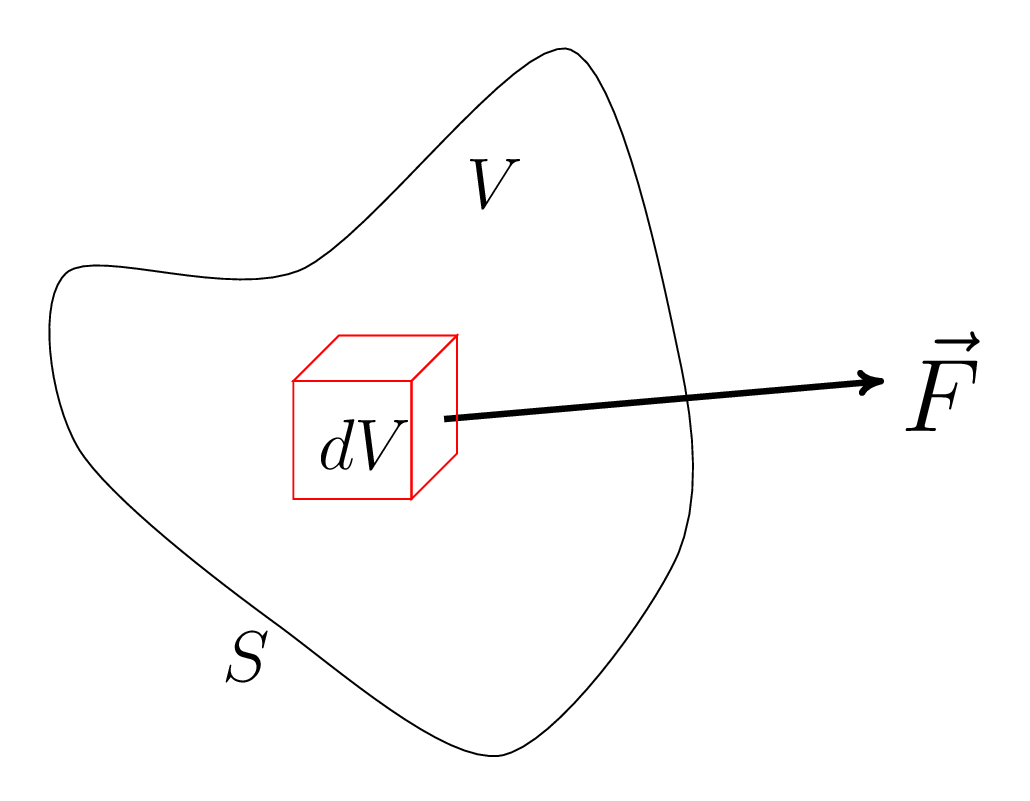
Figure 1.4.3.
Let us consider the volume
\(V\) is enclosed by a closed the surface
\(S\text{,}\) as shown in
Figure 1.4.3 which is lying in the vector field of function
\(\vec{F}\text{,}\) then the
\begin{equation*}
\text{Volume Integral} = \iiint\limits_{V}\vec{F}\,dV.
\end{equation*}
If \(\phi\) is scalar point function in volume \(V\text{,}\) then \(\iiint\phi \,dV\) is a volume integral.