Section 7.3 Heat Equation
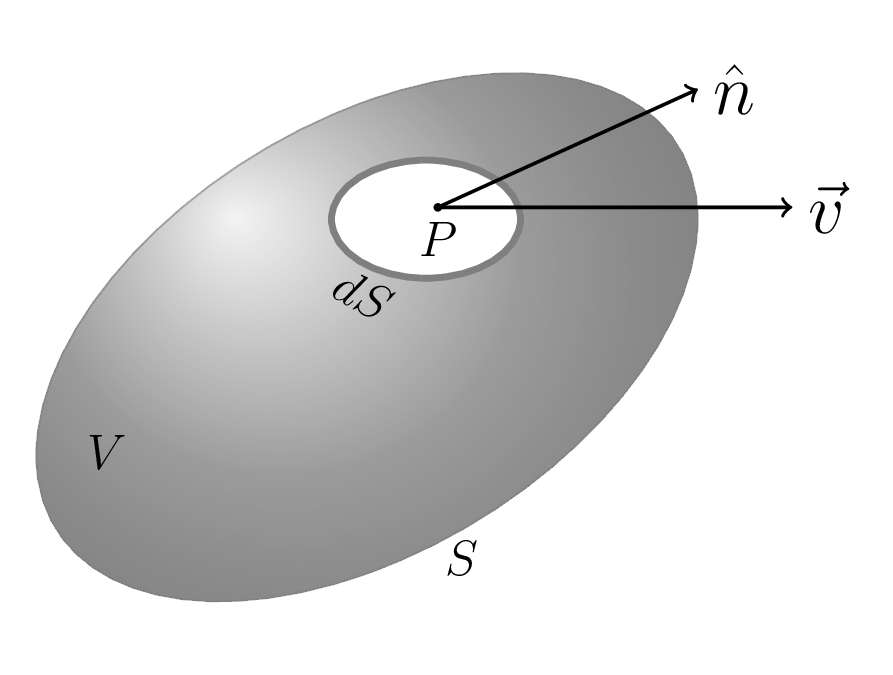
we know that heat flows from hotter region to colder region inside a solid by conduction. Physical experiments reveal that the rate of flow is proportional to the temperature gradient, which implies that the velocity \(v\) of the heat flow in a body is given by \(\vec{v}=-k \,grad \,u =-k \vec{\nabla} u\text{.}\) Where k is a constant, known as thermal conductivity of the body; \(u(x,y,z,t)\) is the temperature at a point P and \(t\) is the time. Now, consider a volume \(V\) of the body enclosed by the boundary surface \(S\text{,}\) as shown in figure Figure 7.3.1. Then the amount of heat leaving the body per unit time is given by
\begin{equation}
-\frac{\partial Q}{\partial t}=\iint\limits_{s}\vec{v}\cdot \hat{n}\,ds\tag{7.3.1}
\end{equation}
But from Gauss’s Divergence Theorem, we have
\begin{equation*}
\iint\limits_{s}\vec{v}\cdot \hat{n}\,ds =\iiint\limits_{V}div\,\vec{v}\,dV
\end{equation*}
where \(V\) is the volume enclosed by surface S.
\begin{equation*}
= \iiint\limits_{V}\vec{\nabla}\cdot\vec{v}\,dV =\iiint\limits_{V}\vec{\nabla}\cdot\left(-k \vec{\nabla} u\right)\,dV
\end{equation*}
\begin{equation}
=-k\iiint\limits_{V}\vec{\nabla}\cdot\vec{\nabla} u\,dV = -k\iiint\limits_{V}\nabla^{2}u\,dV \tag{7.3.2}
\end{equation}
Now if \(\rho\) be the density of the body, \(c\) be the specific heat capacity, then the total heat \(Q\) contained in the body is given by
\begin{equation}
Q=\iiint\limits_{V}c\rho u\,dV \tag{7.3.3}
\end{equation}
\([\because\quad Q = mc\theta =V\rho c \theta ] \) here \(\theta\) = temperature, \(u\)] so the rate of decrease of \(Q\) is given by
\begin{equation}
-\frac{\partial Q}{\partial t}=-\iiint\limits_{V}c\rho \frac{\partial u}{\partial t}\,dV\tag{7.3.4}
\end{equation}
This must be equal to the amount of heat leaving the body in unit time, i.e.,
\begin{equation*}
-\iiint\limits_{V}c\rho \frac{\partial u}{\partial t}\,dV = -k \iiint\limits_{V}\nabla^{2}u\,dV
\end{equation*}
or,
\begin{equation}
\iiint\limits_{V}\left[c\rho \frac{\partial u}{\partial t}-k\nabla^{2}u\right]\,dV=0\tag{7.3.5}
\end{equation}
Since the surface \(S\) is arbitrary, the volume enclosed by surface \(\,dS\) is \(\,dV\neq 0\text{.}\)Thus the integrands must be zero. i.e.,
\begin{equation*}
c\rho \frac{\partial u}{\partial t}= k\nabla^{2}u
\end{equation*}
or,
\begin{equation*}
\frac{\partial u}{\partial t}=\frac{k}{c\rho} \nabla^{2}u
\end{equation*}
\begin{equation}
\therefore \quad \frac{\partial u}{\partial t} =h^{2}\nabla^{2}u\tag{7.3.6}
\end{equation}
This equation is known as heat equation. The quantity \(h^{2}\) is known as diffusivity of the solid, and is defined as the ratio of thermal conductivity and heat capacity of solid per unit volume.
note:
- If there is no heat flow in \(z\)- direction (or temperature of the body is independent of \(z\)), then\begin{equation*} \frac{\partial^{2}u}{\partial z^{2}}=0 \end{equation*}and heat equation\begin{equation} \frac{1}{h^{2}} \frac{\partial u}{\partial t}= \frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}} \tag{7.3.7} \end{equation}is known as heat equation for two - dimensional flow parallel to \(xy\) plane.
- If the flow of heat is only along \(x\)- axis, the heat equation reduces to\begin{equation} \frac{1}{h^{2}} \frac{\partial u}{\partial t}= \frac{\partial^{2}u}{\partial x^{2}} \tag{7.3.8} \end{equation}and is known as the heat equation for one - dimensional flow.
- When the temperature does not change with time (or \(u\) is independent of time) then\begin{equation*} \frac{\partial u}{\partial t} =0 \end{equation*}and equation (7.3.6) reduces to\begin{equation} \nabla^{2}u=0\tag{7.3.9} \end{equation}and is known as heat equation for steady - state flow, which is a famous Laplace’s Equation.
