Appendix D Laplace’s equation in spherical coordinates
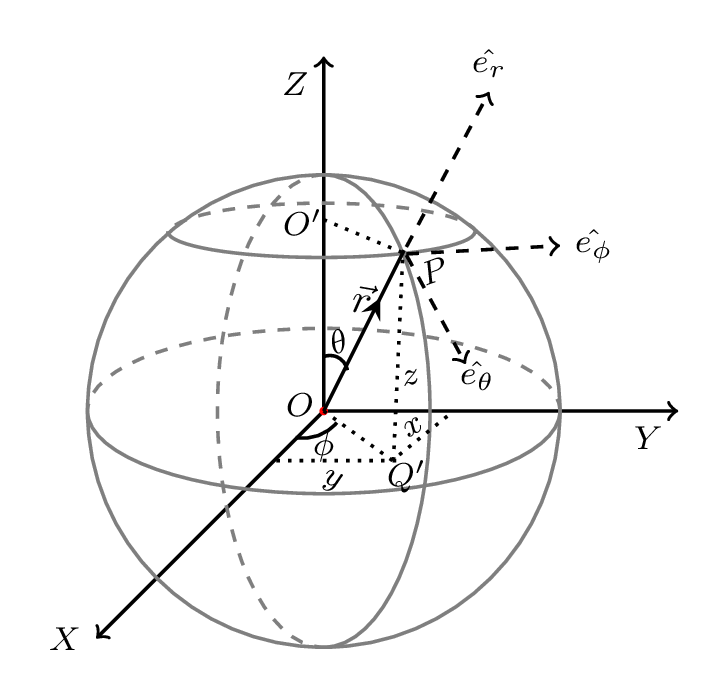
Let us consider a point p having cartesian coordinates \((x,y,z)\) and spherical coordinates \((r,\theta,\phi)\text{,}\) then \(x=r\sin\theta\cos\phi,\) \(y=r\sin\theta\sin\phi, \) and \(z=r\cos\theta\text{,}\) so that,
\begin{equation*}
r^{2}=x^{2}+y^{2}+z^{2},
\end{equation*}
\begin{equation*}
\theta =\tan^{-1}(\frac{\sqrt{x^{2}+y^{2}}}{z}),
\end{equation*}
and
\begin{equation*}
\phi= \tan^{-1}(\frac{y}{x}),
\end{equation*}
also,
\begin{equation*}
\frac{\partial r}{\partial x} =\frac{x}{r}=\sin\theta\cos\phi,
\end{equation*}
\begin{equation*}
\frac{\partial r}{\partial y} =\frac{y}{r}=\sin\theta\sin\phi;
\end{equation*}
\begin{equation*}
\frac{\partial r}{\partial z} =\frac{z}{r}=\cos\theta;
\end{equation*}
\begin{equation*}
\frac{\partial \theta}{\partial x} = \frac{1}{1+(\frac{x^{2}+y^{2}}{z^{2}})}\cdot\frac{1}{z}\cdot\frac{1}{2}\cdot\frac{2x}{\sqrt{x^{2}+y^{2}}}
\end{equation*}
\begin{equation*}
=\frac{zx}{(x^{2}+y^{2}+z^{2})\sqrt{x^{2}+y^{2}}} = \frac{r\cos\theta .r\sin\theta .\cos\phi}{r^{2}.r\sin\theta} = \frac{\cos\theta\cos\phi}{r};
\end{equation*}
\begin{equation*}
\frac{\partial \phi}{\partial x} =\frac{1}{1+\frac{y^{2}}{x^{2}}}\left(-\frac{y}{x^{2}}\right) = -\frac{y}{x^{2}+y^{2}} = -\frac{r\sin\theta\sin\phi}{r^{2}\sin^{2}\theta}= -\frac{\sin\phi}{r\sin\theta};
\end{equation*}
\begin{equation*}
\frac{\partial \theta}{\partial y} =\frac{\cos\theta\sin\phi}{r}; \quad \frac{\partial \theta}{\partial z} =-\frac{\sin\theta}{r};
\end{equation*}
\begin{equation*}
\frac{\partial \phi}{\partial y} = -\frac{\cos\phi}{r\sin\theta}; \quad \frac{\partial \phi}{\partial z} = 0.
\end{equation*}
Now,
\begin{equation*}
\frac{\partial u}{\partial x} =\frac{\partial u}{\partial r}\frac{\partial r}{\partial x}+\frac{\partial u}{\partial \theta}\frac{\partial \theta}{\partial x}+\frac{\partial u}{\partial \phi}\frac{\partial \phi}{\partial x}
\end{equation*}
\begin{equation*}
= \frac{\partial u}{\partial r}\sin\theta\cos\phi+\frac{\partial u}{\partial \theta} \frac{\cos\theta\cos\phi}{r}+\frac{\partial u}{\partial \phi} \left(-\frac{\sin\phi}{r\sin\theta}\right)
\end{equation*}
\begin{equation*}
=\sin\theta\cos\phi \frac{\partial u}{\partial r}+\frac{\cos\theta\cos\phi}{r}\frac{\partial u}{\partial \theta} -\frac{\sin\phi}{r\sin\theta}\frac{\partial u}{\partial \phi}
\end{equation*}
Thus the operator,
\begin{equation*}
\frac{\partial}{\partial x} = \sin\theta\cos\phi \frac{\partial }{\partial r}+\frac{\cos\theta\cos\phi}{r}\frac{\partial }{\partial \theta} -\frac{\sin\phi}{r\sin\theta}\frac{\partial }{\partial \phi};
\end{equation*}
\begin{equation*}
\frac{\partial^{2}u}{\partial x^{2}} =\frac{\partial}{\partial x} \left(\frac{\partial u}{\partial x}\right)
\end{equation*}
\begin{equation*}
=\sin^{2}\theta\cos^{2}\phi \frac{\partial^{2}u}{\partial r^{2}}+\frac{2\sin\theta\cos\theta\cos^{2}\phi}{r}\frac{\partial^{2}u}{\partial r\partial\theta}
\end{equation*}
\begin{equation*}
-\frac{2\sin\theta\cos\theta\cos^{2}\phi}{r^{2}}\frac{\partial u}{\partial\theta}
\end{equation*}
\begin{equation*}
-\frac{2\sin\phi\cos\phi}{r}\frac{\partial^{2}u}{\partial r\partial\phi}+\frac{\cos^{2}\theta\cos^{2}\phi}{r}\frac{\partial u}{\partial r}
\end{equation*}
\begin{equation*}
+\frac{\sin\phi\cos\phi}{r^{2}}\frac{\partial u}{\partial \phi}+\frac{\cos^{2}\theta\cos^{2}\phi}{r^{2}}\frac{\partial^{2}u}{\partial \theta^{2}}
\end{equation*}
\begin{equation*}
-\frac{2\cos\theta\sin\phi\cos\phi}{r^{2}\sin\theta}\frac{\partial^{2}u}{\partial \theta\partial\phi}
\end{equation*}
\begin{equation*}
+\frac{\cos^{2}\theta\sin\phi\cos\phi}{r^{2}\sin^{2}\theta}\frac{\partial u}{\partial\phi}+\frac{\cos\theta\sin^{2}\phi}{r^{2}\sin\theta}\frac{\partial u}{\partial\theta}
\end{equation*}
\begin{equation*}
+\frac{\sin^{2}\phi}{r}\frac{\partial u}{\partial r}
\end{equation*}
\begin{equation}
+\frac{\sin^{2}\phi}{r^{2}\sin^{2}\theta}\frac{\partial^{2}u}{\partial \phi^{2}}+\frac{\sin\phi\cos\phi}{r^{2}\sin^{2}\theta}\frac{\partial u}{\partial \phi} \tag{D.0.1}
\end{equation}
also,
\begin{equation*}
\frac{\partial u}{\partial y}= \frac{\partial u}{\partial r}\frac{\partial r}{\partial y}+\frac{\partial u}{\partial \theta}\frac{\partial \theta}{\partial y}+\frac{\partial u}{\partial \phi}\frac{\partial \phi}{\partial y}
\end{equation*}
\begin{equation*}
= \frac{\partial u}{\partial r}\sin\theta\sin\phi +\frac{\partial u}{\partial \theta}\frac{\cos\theta\sin\phi}{r} +\frac{\partial u}{\partial\phi}\frac{\cos\phi}{r\sin\theta}
\end{equation*}
Thus,
\begin{equation*}
\frac{\partial }{\partial y}\equiv \sin\theta\sin\phi\frac{\partial }{\partial r} +\frac{\cos\theta\sin\phi}{r}\frac{\partial }{\partial \theta} +\frac{\cos\phi}{r\sin\theta}\frac{\partial }{\partial\phi};
\end{equation*}
\begin{equation*}
\therefore \quad \frac{\partial^{2}u}{\partial y^{2}} = \frac{\partial}{\partial y} \left(\frac{\partial u}{\partial y}\right)
\end{equation*}
\begin{equation*}
=\sin^{2}\theta\sin^{2}\phi \frac{\partial^{2}u}{\partial r^{2}}
\end{equation*}
\begin{equation*}
+\frac{2\sin\theta\cos\theta\sin^{2}\phi}{r}\frac{\partial^{2}u}{\partial r\partial\theta}
\end{equation*}
\begin{equation*}
-\frac{2\sin\theta\cos\theta\sin^{2}\phi}{r^{2}}\frac{\partial u}{\partial\theta}
\end{equation*}
\begin{equation*}
+\frac{2\sin\phi\cos\phi}{r}\frac{\partial^{2}u}{\partial r\partial\theta}+\frac{\cos^{2}\theta\sin^{2}\phi}{r}\frac{\partial u}{\partial r}
\end{equation*}
\begin{equation*}
-\frac{\sin\phi\cos\phi}{r^{2}}\frac{\partial u}{\partial \phi}+\frac{\cos^{2}\theta\sin^{2}\phi}{r^{2}}\frac{\partial^{2}u}{\partial \theta^{2}}
\end{equation*}
\begin{equation*}
+\frac{2\cos\theta\sin\phi\cos\phi}{r^{2}\sin\theta}\frac{\partial^{2}u}{\partial \theta\partial\phi}
\end{equation*}
\begin{equation*}
-\frac{\cos^{2}\theta\sin\phi\cos\phi}{r^{2}\sin^{2}\theta}\frac{\partial u}{\partial\phi}+\frac{\cos\theta\cos^{2}\phi}{r^{2}\sin^{2}\theta}\frac{\partial u}{\partial\theta}
\end{equation*}
\begin{equation*}
+\frac{\cos^{2}\phi}{r}\frac{\partial u}{\partial r}
\end{equation*}
\begin{equation}
+\frac{\cos^{2}\phi}{r^{2}\sin^{2}\theta}\frac{\partial^{2}u}{\partial \phi^{2}}-\frac{\sin\phi\cos\phi}{r^{2}\sin^{2}\theta}\frac{\partial u}{\partial \phi} \tag{D.0.2}
\end{equation}
again
\begin{equation*}
\frac{\partial u}{\partial z} =\frac{\partial u}{\partial r}\frac{\partial r}{\partial z}+\frac{\partial u}{\partial \theta}\frac{\partial \theta}{\partial z}+\frac{\partial u}{\partial \phi}\frac{\partial \phi}{\partial z}
\end{equation*}
\begin{equation*}
= \cos\theta \frac{\partial u}{\partial r} - \frac{\sin\theta}{r}\frac{\partial u}{\partial \theta}
\end{equation*}
Hence,
\begin{equation*}
\frac{\partial }{\partial z}\equiv \cos\theta \frac{\partial}{\partial r} - \frac{\sin\theta}{r}\frac{\partial}{\partial \theta}
\end{equation*}
and
\begin{equation*}
\frac{\partial^{2} u}{\partial z^{2}} =\frac{\partial }{\partial z}\left(\frac{\partial u}{\partial z}\right)
\end{equation*}
\begin{equation*}
=\cos^{2}\theta\frac{\partial^{2} u}{\partial r^{2}}-\frac{2\sin\theta\cos\theta}{r} \frac{\partial^{2} u}{\partial r\partial\theta}
\end{equation*}
\begin{equation}
+\frac{2\sin\theta\cos\theta}{r^{2}} \frac{\partial u}{\partial r}+\frac{\sin^{2}\theta}{r}\frac{\partial }{\partial r}+\frac{\sin^{2}\theta}{r^{2}}\frac{\partial^{2} u}{\partial \theta^{2}} \tag{D.0.3}
\end{equation}
\begin{equation*}
\frac{\partial^{2} u}{\partial x^{2}}+ \frac{\partial^{2} u}{\partial y^{2}} + \frac{\partial^{2} u}{\partial z^{2}}
\end{equation*}
\begin{equation*}
= \frac{\partial^{2} u}{\partial r^{2}}+\frac{2}{r}\frac{\partial u}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}}+\frac{\cot\theta}{r^{2}}\frac{\partial u}{\partial \theta}+\frac{1}{r^{2}\sin^{2}\theta}\frac{\partial^{2} u}{\partial \phi^{2}}.
\end{equation*}
Thus the Laplace’s differential equation in spherical coordinates is given by
\begin{equation*}
\frac{\partial^{2} u}{\partial r^{2}}+\frac{2}{r}\frac{\partial u}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} u}{\partial \theta^{2}}+\frac{\cot\theta}{r^{2}}\frac{\partial u}{\partial \theta}+\frac{1}{r^{2}\sin^{2}\theta}\frac{\partial^{2} u}{\partial \phi^{2}} =0
\end{equation*}
or,
\begin{equation*}
\frac{1}{r^{2}}\frac{\partial }{\partial r}\left(r^{2}\frac{\partial u}{\partial r}\right)+\frac{1}{r^{2}\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial u}{\partial \theta}\right)+\frac{1}{r^{2}\sin^{2}\theta}\frac{\partial^{2} u}{\partial \phi^{2}} =0.
\end{equation*}
