Skip to main content

Mathematical Methods of Physics: For Undergraduate

Sunil Karna

Section 4.2 ExamplesA

Example 4.2.1.

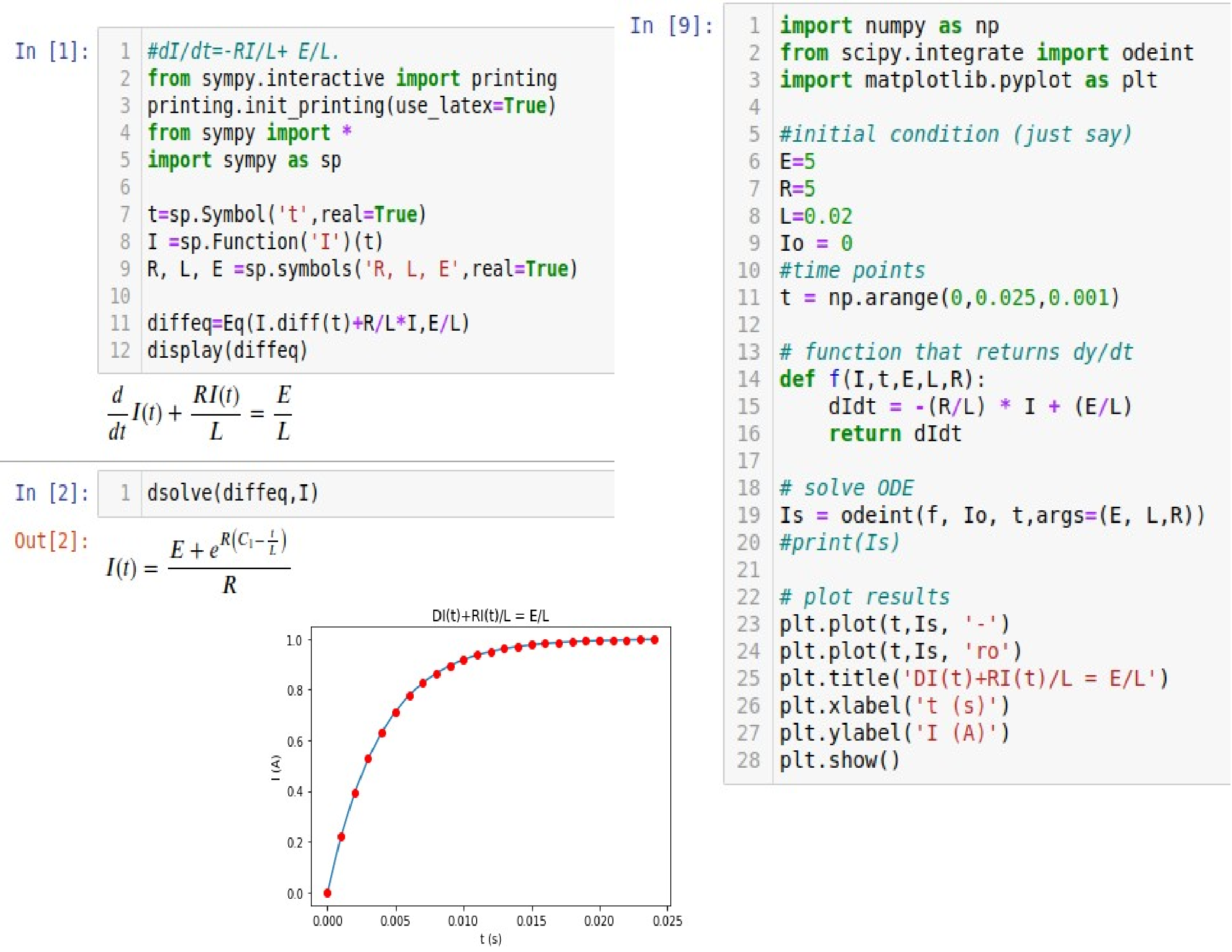
The current in a circuit, containing a resistance \(R\text{,}\) an induction \(L\text{,}\) and a constant e.m.f. \(E\text{,}\) at time \(t\text{,}\) is given by \(i=\frac{E}{R}\left(1-e^{-\frac{Rt}{L}}\right)\text{.}\) Obtain a suitable approximation to \(i\) when \(t\) is very small.
Solution.
From a circuit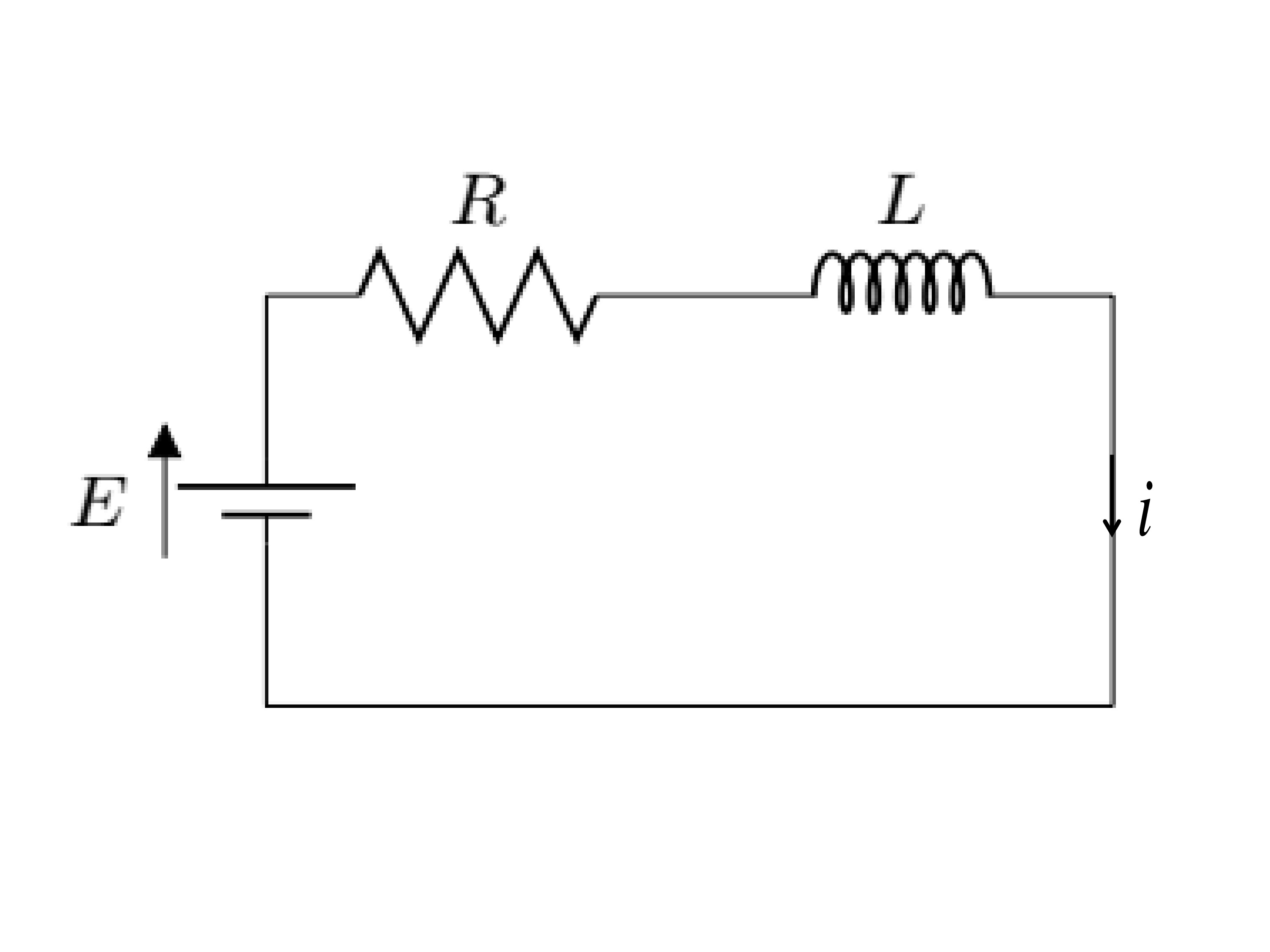
, we have potential drop across resistance \(=iR\) and voltage induced at inductance \(=-L\frac{\,di}{\,dt} \text{.}\) Using Kirchoff’s Voltage law,
\begin{equation*} E-L\frac{\,di}{\,dt} = iR \end{equation*}
or,
\begin{equation*} \frac{\,di}{\,dt}+\frac{Ri}{L}=\frac{E}{L} \end{equation*}
or,
\begin{equation*} I.F. = e^{\int \frac{R}{L}\,dt}=e^{\frac{Rt}{L}} \end{equation*}
Its solution is
\begin{equation*} i\cdot e^{\frac{Rt}{L}} = \int \frac{E}{L}e^{\frac{Rt}{L}}\,dt+C =\frac{E}{L}\cdot\frac{L}{R}e^{\frac{Rt}{L}}+C \end{equation*}
\begin{equation} \therefore \quad i=\frac{E}{R}+Ce^{-\frac{Rt}{L}} \tag{4.2.1} \end{equation}
when \(t=0,\quad i=0 \) then, \(0=\frac{E}{R}+C\) or, \(C=-\frac{E}{R}\text{.}\) Therefore, expression (4.2.1) becomes
\begin{equation*} i=\frac{E}{R}-\frac{E}{R}e^{-\frac{Rt}{L}} = \frac{E}{R}\left(1-e^{-\frac{Rt}{L}}\right) \end{equation*}
but, when \(t = \infty,\)
\begin{equation*} i=\frac{E}{R}. \qquad \text{ans.} \end{equation*}

Example 4.2.2.

Find the solution for the equation of motion when a mass \(m\) attached to a spring with spring constant \(k\) is pulled and then released, as shown in figure
Solution.
The motion executed by a spring is simple harmonic motion, therefore, \(F=-ky\) (where \(y\) is the displacement of mass \(m\) at any time, \(t\text{.}\))
\begin{equation*} m\frac{\,d^{2}y}{\,dt^{2}}=-ky \end{equation*}
or,
\begin{equation*} \frac{\,d^{2}y}{\,dt^{2}}+\frac{k}{m}y=0 \end{equation*}
or,
\begin{equation} \frac{\,d^{2}y}{\,dt^{2}}+\omega^{2}y=0\tag{4.2.2} \end{equation}
where \(\omega^{2} = \frac{k}{m}\text{.}\) The eqn. (4.2.2) is the equation of motion.
\begin{equation*} A.E. = m^{2}+\omega^{2}=0 \hspace{0.5cm} \text{or,} \quad m=\pm i\omega \end{equation*}
The general solution of eqn. (4.2.2) is then
\begin{equation} y(t) =C_{1}e^{i\omega}t+C_{2}e^{-i\omega}t = A\cos\omega t+B\sin\omega t\tag{4.2.3} \end{equation}
If \(T\) be the period of motion, then \(y(t)=y(t+T)\text{.}\)
\begin{equation*} \therefore A \cos\omega t +B\sin\omega t =A\cos(\omega t+\omega T)+B\sin(\omega t+\omega t) \end{equation*}
\begin{equation*} = A\left[\cos\omega t\cdot\cos\omega T-\sin\omega t\cdot\sin\omega T\right] + B\left[\sin\omega t\cdot\cos\omega T+\cos\omega t\cdot\sin\omega T\right] \end{equation*}
\begin{equation*} =\left(A\cos\omega T+B\sin\omega T\right)\cos\omega t+\left(B\cos\omega T-A\sin\omega T\right)\sin\omega t \end{equation*}
equating on both sides, we get -
\begin{equation*} A\cos\omega T+B\sin\omega T = A \end{equation*}
\begin{equation*} \Rightarrow \cos\omega T =1 \hspace{1cm} \text{and} \quad \sin\omega T =0. \end{equation*}
i.e.,
\begin{equation*} \cos\omega T =1=\cos 2n\pi \end{equation*}
or,
\begin{equation*} \omega T = 2n\pi \end{equation*}
\begin{equation*} \therefore T = \frac{2n\pi}{\omega} = 2n\pi\sqrt{\frac{m}{k}} \end{equation*}

Example 4.2.3.

Solve
\begin{equation*} \frac{\,d^{2}y}{\,dx^{2}}+a^{2}y=\sec ax. \end{equation*}
Solution.
A.E. is \(D^{2}+a^{2}=0\) or, \(D=\pm ai\text{.}\)
\begin{equation*} C.F. = C_{1}\cos ax+C_{2}\sin ax \end{equation*}
\begin{equation*} P.I. = \frac{1}{D^{2}+a^{2}}\cdot \sec ax = \frac{1}{(D+ai)(D-ai)}\cdot \sec ax \end{equation*}
\begin{equation*} = \frac{1}{2ai}\left[\frac{1}{(D-ai)}-\frac{1}{(D+ai)}\right]\sec ax \end{equation*}
Therefore,
\begin{equation} P.I. = \frac{1}{2ai}\frac{1}{(D-ai)}\sec ax-\frac{1}{2ai}\frac{1}{(D+ai)}\sec ax \tag{4.2.4} \end{equation}
Now,
\begin{equation} \frac{1}{(D-ai)}\sec ax = e^{aix}\int e^{-aix}\sec ax\,dx\tag{4.2.5} \end{equation}
[using eqns. (4.1.17), and (4.1.18)]
\begin{equation*} =e^{aix}\int\frac{\cos ax-i\sin ax}{\cos ax}\,dx =e^{aix}\int(1-i\tan ax)\,dx \end{equation*}
\begin{equation*} = e^{aix}(x+\frac{i}{a}\log\cos ax) \end{equation*}
changing \(i\) to \(-i\text{,}\) we have
\begin{equation*} \frac{1}{(D+ai)}\sec ax =e^{-aix}(x-\frac{i}{a}\log\cos ax) \end{equation*}
putting these values in eqn. (4.2.4), we get -
\begin{equation*} P.I. = \frac{1}{2ai}\left[e^{aix}\left(x+\frac{i}{a}\log\cos ax\right)-e^{-aix}\left(x-\frac{i}{a}\log\cos ax\right)\right] \end{equation*}
\begin{equation*} =\frac{x}{2ai}e^{aix}-\frac{x}{2ai}e^{-aix}+\frac{e^{aix}\log\cos ax}{2a^{2}}+\frac{e^{-aix}\log\cos ax}{2a^{2}} \end{equation*}
\begin{equation*} =\frac{x}{a}\frac{e^{aix}-e^{-aix}}{2i}+\frac{1}{a^{2}}\frac{e^{aix}+e^{-aix}}{2}\log\cos ax \end{equation*}
\begin{equation*} =\frac{x}{a}\sin ax +\frac{1}{a^{2}}\cos ax\cdot\log\cos ax \end{equation*}
\begin{equation*} \therefore y= C_{1}\cos ax+C_{2}\sin ax+\frac{x}{a}\sin ax+\frac{1}{a^{2}}\cos ax\cdot\log\cos ax. \end{equation*}

Example 4.2.4.

Solve
\begin{equation*} \frac{\,d^{2}y}{\,dx^{2}}-2\frac{\,dy}{\,dx}+y=2\cos x. \end{equation*}
Solution.
\begin{equation} (D^{2}-2D+1)y =2\cos x \tag{4.2.6} \end{equation}
\begin{equation*} \text{A.E.,} \quad m^{2}-2m+1=0 \end{equation*}
or,
\begin{equation*} (m-1)^{2}=0 \quad \Rightarrow m=1,1 \end{equation*}
\begin{equation} \therefore \quad C.F. = y_{c} = (C_{1}+C_{2}x)e^{x} \tag{4.2.7} \end{equation}
\begin{equation} \text{P.I.} = y_{p} \quad \text{(By inspection method)}\tag{4.2.8} \end{equation}
Let, \(y_{p} =-\sin x,\) \(Dy_{p}=-\cos x\text{,}\) and, \(D^{2} y_{p} =\sin x\text{.}\) Therefore, \(y=y_{p}\) is a P.I. of eqn. (4.2.6), becouse it satisfies the equation.
\begin{equation} y=y_{c}+y_{p}=(C_{1}+C_{2}x)e^{x}-\sin x \tag{4.2.9} \end{equation}
It is a general solution of eqn. (4.2.6).
The solution of eqn. (4.2.6) by successive integration method. The roots of A.E. are real and equal, i.e., \(m=1,1\text{.}\) Hence, from eqn. (4.1.19)
\begin{equation} y= e^{x}\int \bar{Q}(x)e^{-x}\,dx +C_{2}e^{x} \tag{4.2.10} \end{equation}
where,
\begin{equation} \bar{Q}(x) =2e^{x}\int e^{-x}\cos x\,dx+C_{1}e^{x} \tag{4.2.11} \end{equation}
using (4.1.20). Hence,
\begin{equation*} \int e^{-x}\cos x\,dx=\frac{e^{-x}(\sin x-\cos x)}{1+1}=\frac{e^{-x}(\sin x-\cos x)}{2} \end{equation*}
\begin{equation*} \because \quad \int e^{mx}\cos nx\,dx=\frac{e^{mx}(n\sin nx+m\cos nx)}{m^{2}+n^{2}} \end{equation*}
and
\begin{equation*} \int e^{mx}\sin nx\,dx=\frac{e^{mx}(m\sin nx-n\cos nx)}{m^{2}+n^{2}} \end{equation*}
or,
\begin{equation*} \bar{Q}(x)=e^{x}.e^{-x}(\sin x-\cos x)+C_{1}e^{x} \end{equation*}
\begin{equation*} \therefore y=e^{x}\int \left\{\left(\sin x-\cos x\right)+C_{1}e^{x}\right\}e^{-x}\,dx +C_{2}e^{x} \end{equation*}
\begin{equation*} =e^{x}\left[\int e^{-x}\sin x\,dx-\int e^{-x}\cos x\,dx+C_{1}\int\,dx\right]+C_{2}e^{x} \end{equation*}
\begin{equation*} =e^{x}\left[\frac{e^{-x}(-\sin x-\cos x)}{2}-\frac{e^{-x}(\sin x-\cos x)}{2}+C_{1}x\right]+C_{2}e^{x} \end{equation*}
\begin{equation*} =\frac{(-\sin x-\cos x)}{2}-\frac{(\sin x-\cos x)}{2}+C_{1}xe^{x}+C_{2}e^{x} \end{equation*}
\begin{equation*} =(C_{1}x+C_{2})e^{x}-\sin x. \qquad \text{ans}. \end{equation*}

Python Code for Differential Equation.

  1. For equation
    \begin{equation*} \frac{\,di}{\,dt}+\frac{Ri}{L}=\frac{E}{L} \end{equation*}
    the Python code is
    from sympy.interactive import printing
    printing.init_printing(use_latex=True)
    from sympy import *
    import sympy as sp
    t=sp.Symbol(’t’, real=True)
    I=sp.Function(’I’)(t)
    R, L, E=sp.symbols(’R, L, E’, real=True)
    diffeq=Eq(I.diff(t)+R/L*I,E/L)
    display(diffeq)
    dsolve(diffeq,I)
    import numpy as np
    from scipy.integrate import odeint
    import matplotlib.pyplot as plt
    E=5
    R=5
    L=0.02
    Io=0
    t=np.arange(0,0.025,0.001)
    def f(I,t,E,L,R):
    dIdt =-(R/L)*I+(E/L)
    return dIdt
    Is=odeint(f,Io,t,args=(E,L,R))
    plt.plot(t,Is, ’-’)
    plt.plot(t,Is, ’ro’)
    plt.title(’DI(t)+RI(t)/L=E/L’)
    plt.xlabel(’t(s)’)
    plt.ylabel(’I(A)’)
    plt.show()
    Since \(e^{RC_{1}}\) is a constant, the general solution of this equation is \(I(t) = \left[\frac{E}{R}+Ce^{-Rt/L}\right]\text{.}\)
  2. \(y"+a^2*y=0\)
    from sympy.interactive import printing
    printing.init_printing(use_latex=True)
    from sympy import *
    import sympy as sp
    t,y =sp.symbols(’t,y’)
    a=sp.Symbol(’a’,positive=True)
    y=sp.Function(’y’)(t)
    diffeq=Eq(y.diff(t,2)+a**2*y,0)
    display(diffeq)
    dsolve(diffeq,y)
    import numpy as np
    from scipy.integrate import odeint
    import matplotlib.pyplot as plt
    def f(u,t): return (u[1], -5*u[0])
    yo=[0,4]
    xs=np.arange(0,5,0.1)
    us=odeint(f,yo,xs)
    ys=us[:,0]
    plt.plot(xs,ys, ’-’)
    plt.plot(xs,ys, ’ro’)
    plt.title(’(D**2+5)y=0’)
    plt.xlabel(’t values’)
    plt.ylabel(’y values’)
    plt.show()
  3. \(y"+a^2*y=\sec(ax)\)
  4. \(y"-2y'+y=2*\cos(x)\)

Example 4.2.5.

Solve
\begin{equation*} x^{2}y''-(x^{2}+2x)y'+(x+2)y=x^{3}\text{.} \end{equation*}
Solution.
The equation in standard form is
\begin{equation} y''-\left(1+\frac{2}{x}\right)y' +\left(\frac{1}{x}+\frac{2}{x^{2}}\right)y=x \tag{4.2.12} \end{equation}
Here, \(P=-\left(1+\frac{2}{x}\right) \) and \(Q= \left(\frac{1}{x}+\frac{2}{x^{2}}\right)\text{.}\) Since, \(P+Qx=0\text{,}\) we have \(y_{1} =x \) is a known integral of C.F. So we find C.F. of the given differential eqn. (4.2.12) by putting \(y=vx\) in
\begin{equation} y''-\left(1+\frac{2}{x}\right)y' +\left(\frac{1}{x}+\frac{2}{x^{2}}\right)y=0 \tag{4.2.13} \end{equation}
or,
\begin{equation*} \frac{d^{2}v}{dx^{2}}-\frac{dv}{dx}=0 \end{equation*}
or,
\begin{equation*} [D^{2}-D]v =0, \end{equation*}
\begin{equation*} \therefore \quad D =0,1. \end{equation*}
Hence, \(v=C_{1}+C_{2}e^{x}\) [\(\because C.F.= C_{1}e^{m_{1}x}+C_{2}e^{m_{2}x}\)]. Therefore the C.F. of eqn. (4.2.13) is \(y=vx=C_{1}x+C_{2}xe^{x} \text{,}\) where, \(y_{1} =x {,} y_{2}=xe^{x}\text{,}\) and \(|W| =y_{1}y'_{2} -y'_{1} y_{2} =x^{2}e^{x}\text{.}\) Now, let \(y=v_{1}y_{1}+v_{2}y_{2} = v_{1}x+v_{2}xe^{x}\) be the solution of eqn. (4.2.12). Where,
\begin{equation*} v_{1}=-\int \frac{Xy_{2}}{|W|}\,dx+C_{1} =-x+C_{1} \end{equation*}
and
\begin{equation*} v_{2}=\int \frac{Xy_{1}}{|W|}\,dx+C_{2} =-e^{-x}+C_{2} \end{equation*}
Therefore the complete solution is
\begin{equation*} y=(-x+C_{1})x+(-e^{-x}+C_{2})xe^{x}=(C_{1}x+C_{2}xe^{x})-(x^{2}+x). \end{equation*}

Example 4.2.6.

Solve
\begin{equation*} x^{2}y''-2xy'+2y=x\ln{x}\text{.} \end{equation*}
Solution.
The equation in standard form is
\begin{equation} y''-\frac{2}{x}y' +\frac{2}{x^{2}}y =\frac{\ln{x}}{x}\tag{4.2.14} \end{equation}
Since \(P+Qx=0\) and \(2+2Px+Qx^{2} =0 \) we assume \(y_{1}=x\) and \(y_{2}=x^{2}\) to be the two independent solutions of eqn. (4.2.14). Hence we have \(|W|=x^{2}\text{.}\) Therefore the complete solution of eqn. (4.2.14) is [see eqn. (4.1.33)]
\begin{equation*} y=x\left[-\int\frac{x^{2}\left(\frac{\ln{x}}{x}\right)}{x^{2}}\,dx+C_{1}\right]+x^{2}\left[\int\frac{x\left(\frac{\ln{x}}{x}\right)}{x^{2}}\,dx+C_{2}\right] \end{equation*}
\begin{equation*} =-x\int\left(\frac{\ln{x}}{x}\right)\,dx+C_{1}x+x^{2}\int\left(\frac{\ln{x}}{x^{2}}\right)\,dx+C_{2}x^{2} \end{equation*}
\begin{equation*} =-x\left\{\frac{1}{2}(\ln x)^{2}\right\}+x^{2}\left\{-\frac{\ln x}{x}-\frac{1}{x}\right\}+(C_{1}x+C_{2}x^{2}) \end{equation*}
\begin{equation*} =-x\left\{\frac{1}{2}(\ln x)^{2}+\ln x+1\right\}+(C_{1}x+C_{2}x^{2}). \end{equation*}

Example 4.2.7.

Solve
\begin{equation*} x^{2}y''+xy' - y=x^{2}e^{x}. \end{equation*}
Solution.
\begin{equation} x^{2}y''+xy' - y=x^{2}e^{x} \tag{4.2.15} \end{equation}
This is the equation with decreasing power of x. Hence put \(x=e^{z}\) and \(\frac{d}{dz}\equiv D\text{.}\) We have
\begin{equation*} D(D-1)y+Dy-y=e^{2z}e^{e^{z}} \end{equation*}
or,
\begin{equation} (D^{2}-1)y=e^{2z}e^{e^{z}}\tag{4.2.16} \end{equation}
A.E. is
\begin{equation*} D^{2}-1 =0 \end{equation*}
or,
\begin{equation*} D=+1,-1 \end{equation*}
\begin{equation} \text{C.F.} = C_{1}e^{z}+C_{2}e^{-z} = C_{1}x+\frac{C_{2}}{x} \tag{4.2.17} \end{equation}
where \(y_{1}=x\) and \(y_{2}=\frac{1}{x}\) also
\begin{equation*} |W| =y_{1}y'_{2} -y'_{1}y_{2} = x(-\frac{1}{x^{2}})-1.\frac{1}{x} =-\frac{2}{x} \end{equation*}
The standard form of eqn. (4.2.15) is
\begin{equation} y'' +\frac{1}{x}y'-\frac{1}{x^{2}}y = e^{x} \tag{4.2.18} \end{equation}
Now the complete solution of eqn. (4.2.18) is
\begin{equation*} y=x\left[-\int\frac{e^{x}.\frac{1}{x}}{-\frac{2}{x}}\,dx +C_{1}\right]+\frac{1}{x}\left[\int\frac{e^{x}.x}{-\frac{2}{x}}\,dx+C_{2}\right] \end{equation*}
 1 
If \(x=e^{z}\) then \(z=\log x\) and \(\frac{\,dz}{\,dx}=\frac{1}{x} \) hence,
\begin{equation*} \frac{\,dy}{\,dx} =\frac{\,dy}{\,dz}\cdot \frac{\,dz}{\,dx} =\frac{1}{x}\cdot \frac{\,dy}{\,dz} \end{equation*}
or,
\begin{equation*} x\frac{\,dy}{\,dx}=\frac{\,dy}{\,dz}=Dy \end{equation*}
also,
\begin{equation*} x^{2}\frac{\,d^{2}y}{\,dx^{2}} \end{equation*}
\begin{equation*} = \frac{\,d^{2}y}{\,dz^{2}}-\frac{\,dy}{\,dz}=D^{2}y-Dy =D(D-1)y \end{equation*}
\begin{equation*} =x\left[\frac{e^{x}}{2}+C_{1}\right]+\frac{1}{x}\left[-\frac{1}{2}e^{x}x^{2}+xe^{x}-e^{x}+C_{2}\right] \end{equation*}
\begin{equation*} = (C_{1}x+\frac{C_{2}}{x})+(e^{x}-\frac{e^{x}}{x}) \end{equation*}

Example 4.2.8.

Solve
\begin{equation*} y''-2y' - 3y=\sin(2x) \end{equation*}
Solution.
It has \(1-P+Q=0\) type auxiliary equaion, hence \(y_{1} =e^{-x}\) be the known integral of C.F. Select \(y=vy_{1}\) be the solutioin of corresponding differential equation. (read page Subsubsection 4.1.2.3 for details). We may get a homogeneous equation like \(v''-2v'=0\) which gives, \(D=\pm\sqrt{2}.\) This corresponds to \(C.F. = C_{1}e^{m_{1}x}+C_{2}e^{m_{2}x}.\) Use Wronskian to find the complete solution of the differential equation.
PrevTopNext