ExamplesB

Section 7.4 ExamplesB

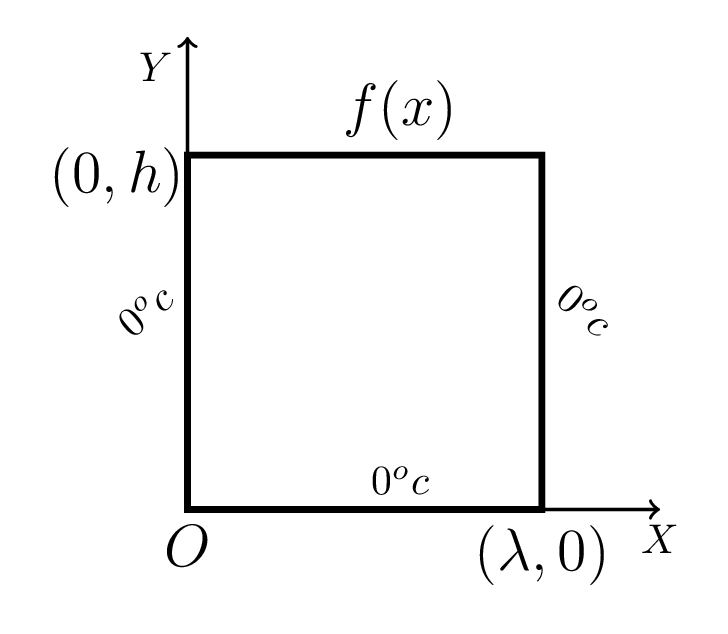
Example 7.4.1.

Find the temperature distribution in the bar if bar and its ends are perfactly insulated, i.e.,

\begin{equation*} \left.\frac{\partial u}{\partial x}\right\vert_{(0,t)} =0= \left.\frac{\partial u}{\partial x}\right\vert_{(\lambda,t)} \end{equation*}

and initial temperature is \(u(x,0)=f(x)\text{.}\)

Solution.

Let the heat eqn. is

\begin{equation} \frac{\partial u}{\partial t} =h^{2}\frac{\partial^{2}u}{\partial x^{2}} \tag{7.4.1} \end{equation}

and

\begin{equation} u(x,t)=X(x)T(t) \tag{7.4.2} \end{equation}

be the solution of eqn. (7.4.1). Then by making substitution of eqn. (7.4.2) into eqn. (7.4.1), we get the solution as

\begin{equation} u(x,t) = (A\cos\lambda x+B\sin\lambda x)Ce^{-\lambda^{2}h^{2}t} \tag{7.4.3} \end{equation}

or,

\begin{equation} \frac{\partial u}{\partial x}=-A\lambda \sin\lambda x+B\lambda\cos\lambda x)Ce^{-\lambda^{2}h^{2}t} \tag{7.4.4} \end{equation}

putting \(\frac{\partial u}{\partial x}=0 \) at \(x=0\) in eqn. (7.4.4), we get -

\begin{equation*} 0=B\lambda Ce^{-\lambda^{2}h^{2}t} \Rightarrow B=0. \end{equation*}

Therefore, eqn. (7.4.3) reduces to

\begin{equation} u(x,t) = (A\cos\lambda x)Ce^{-\lambda^{2}h^{2}t} \tag{7.4.5} \end{equation}

and

\begin{equation} \frac{\partial u}{\partial x} =-A\lambda \sin\lambda x Ce^{-\lambda^{2}h^{2}t} \tag{7.4.6} \end{equation}

putting

\begin{equation*} \frac{\partial u}{\partial x}= 0 \end{equation*}

at \(x=\lambda \) in eqn. (7.4.6), we have -

\begin{equation*} 0=-AC\lambda\sin\lambda\lambda e^{-\lambda^{2}h^{2}t} \Rightarrow \sin\lambda\lambda =0=\sin n\pi \end{equation*}

or,

\begin{equation*} \lambda\lambda =n\pi \end{equation*}

or,

\begin{equation} \lambda=\frac{n\pi}{\lambda} \quad \text{where} \quad n=1,2,3,\cdots \tag{7.4.7} \end{equation}

on putting the value of \(\lambda\) in eqn. (7.4.5), we have -

\begin{equation} u(x,t) = (AC\cos\frac{n\pi x}{\lambda})e^{-n^{2}\pi^{2}h^{2}t/\lambda^{2}} = \sum\limits_{n=1}^{\infty}b_{n}\cos\frac{n\pi x}{\lambda}e^{-n^{2}\pi^{2}h^{2}t/\lambda^{2}} \tag{7.4.8} \end{equation}

which is the required solution of eqn. (7.4.1). Now, for initial condition, eqn. (7.4.8) becomes

\begin{equation} u(x,0) =f(x) = \sum\limits_{n=1}^{\infty}b_{n}\cos\frac{n\pi x}{\lambda} \tag{7.4.9} \end{equation}

and

\begin{equation} b_{n}=\frac{2}{\lambda}\int\limits_{0}^{\lambda}f(x) \cos\frac{n\pi x}{\lambda}\,dx \tag{7.4.10} \end{equation}

Example 7.4.2.

A rod of length \(\lambda\) with insulated sides is initially at a uniform temperature \(u\text{.}\) Its ends are suddenly cooled to \(0^{o} C\) and maintained at this temperature. Prove that the temperature function \(u\) is given by

\begin{equation*} u(x,t) = \sum\limits_{n=1}^{\infty}b_{n}\sin \frac{n\pi x}{\lambda}e^{-n^{2}\pi^{2}h^{2}t/\lambda^{2}}. \end{equation*}

where \(b_{n} \) is determined from the equation

\begin{equation*} u_{o}= \sum\limits_{n=1}^{\infty}b_{n}\sin \frac{n\pi x}{\lambda}. \end{equation*}

Solution.

Let the heat equation be

\begin{equation} \frac{\partial u}{\partial t} =h^{2}\frac{\partial^{2}u}{\partial x^{2}}\tag{7.4.11} \end{equation}

and solution of which is given by

\begin{equation} u(x,t)=X(x)T(t) =(A\cos\lambda x+B\sin\lambda x)Ce^{-\lambda^{2}h^{2}t} \tag{7.4.12} \end{equation}

The boundary conditions \(u=0\) at \(x=0\text{,}\) we get -

\begin{equation*} 0= ACe^{-\lambda^{2}h^{2}t} \Rightarrow A=0 \quad \text{since}\quad C\neq 0. \end{equation*}

again, \(u=0\) at \(x=\lambda\text{,}\) we have -

\begin{equation*} 0=Ce^{-\lambda^{2}h^{2}t}\cdot B\sin\lambda\lambda, \end{equation*}

since \(B\) can not be zero. or,

\begin{equation*} \sin\lambda\lambda = 0=\sin n\pi \Rightarrow \lambda = \frac{n\pi}{\lambda}, \end{equation*}

where \(n=1,2,3,\cdots \text{.}\) Now eqn. (7.4.12) becomes -

\begin{equation*} u=BC\sin\frac{n\pi x}{\lambda}e^{-n^{2}\pi^{2}h^{2}t/\lambda^{2}} \end{equation*}

\begin{equation} =\sum\limits_{n=1}^{\infty}b_{n}\sin \frac{n\pi x}{\lambda}e^{-n^{2}\pi^{2}h^{2}t/\lambda^{2}} \tag{7.4.13} \end{equation}

which is the required solution of eqn. (7.4.11). By initial condition \(u=u_{o} \) at \(t=0\text{,}\) we have-

\begin{equation*} u_{o}=\sum\limits_{n=1}^{\infty}b_{n}\sin \frac{n\pi x}{\lambda} \end{equation*}

Laplace Equation.

Example 7.4.3.

A rectangular plate bounded by the lines \(x=0,y=0,x=a,y=b\) has an initial distribution of temperature given by

\begin{equation*} f(x,y)=B\sin\frac{\pi x}{a}\sin\frac{\pi y}{b}. \end{equation*}

Solution.

The general solution is given as

\begin{equation*} u(x,y,t)=\sum\limits_{r,s=1}^{\infty}a_{rs}e^{-m_{rs}t}\sin\frac{r\pi x}{a}\sin\frac{s\pi y}{b} \end{equation*}

where

\begin{equation*} a_{rs} =\frac{4}{ab}\int\limits_{0}^{a}\int\limits_{0}^{b}f(x,y)\sin\frac{r\pi x}{a}\sin\frac{s\pi y}{b}\,dx\,dy \end{equation*}

\begin{equation*} = \frac{4B}{ab}\int\limits_{0}^{a}\int\limits_{0}^{b}\sin\frac{\pi x}{a}\sin\frac{\pi y}{b}\sin\frac{r\pi x}{a}\sin\frac{s\pi y}{b}\,dx\,dy \end{equation*}

\begin{equation*} \therefore \quad a_{r1}= \frac{4B}{ab}\int\limits_{0}^{a}\frac{b}{2}\sin\frac{\pi x}{a}\sin\frac{r\pi x}{a}\,dx \end{equation*}

\begin{equation*} \because \quad \int\limits_{0}^{b}\sin\frac{\pi y}{b}\sin\frac{s\pi y}{b}\,dy = \begin{cases} 0, & n=2,3,4,\cdots\\ b/2, & n=1 \end{cases} \end{equation*}

so that \(a_{11}=B\) and

\begin{equation*} m_{11}=h^{2}\pi^{2}\left(\frac{1}{a^{2}}+\frac{1}{b^{2}}\right) \end{equation*}

Hence the solution is

\begin{equation*} u(x,y,t) =a_{11}e^{-m_{11}t}\cdot \sin\frac{\pi x}{a}\sin\frac{\pi y}{b}. \end{equation*}

Example 7.4.4.

Determine the steady state temperature in a rectangular plate of length \(a\) and width \(b\) with sides maintained at a temperature zero while the lower end is kept at temperature \(f(x) \) and the upper one is insulated.

Solution.

The equation of steady state heat flow is given by

\begin{equation*} \frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}} =0 \end{equation*}

The boundary conditions are given as

\begin{equation*} u(0,y) =0=u(a,y), \end{equation*}
\begin{equation*} u(x,y) =f(x), \end{equation*}
\begin{equation*} u_{y}(x,b)=0. \end{equation*}

The solution of this problem is obtained as

\begin{equation*} u(x,y) = \sum\limits_{n=1}^{\infty}\left[C_{n}\cosh\frac{n\pi y}{a}+D_{n}\sinh\frac{n\pi y}{a}\right] \sin \frac{n\pi x}{a} \end{equation*}

from condition (iii), we have -

\begin{equation*} f(x)= \sum\limits_{n=1}^{\infty}C_{n}\sin\frac{n\pi x}{a}\quad \text{so that }\quad C_{n} =\frac{2}{a}\int\limits_{0}^{a}f(x) \sin \frac{n\pi x}{a}\,dx \end{equation*}

and from condition (iv) -

\begin{equation*} 0=u_{y}(x,b) = \sum\limits_{n=1}^{\infty}\frac{n\pi}{a}\left(C_{n}\sinh\frac{n\pi b}{a} + D_{n}\cosh\frac{n\pi b}{a}\right)\sin\frac{n\pi x}{a} \end{equation*}

\begin{equation*} \Rightarrow D_{n} = -C_{n}\tanh\frac{n\pi b}{a}. \end{equation*}

Hence,

\begin{equation*} u(x,y) = \frac{2}{a}\sum\limits_{n=1}^{\infty}\left(\cosh\frac{n\pi y}{a}-\tanh\frac{n\pi y}{a}\sin\frac{n\pi y}{a}\right)\sin\frac{n\pi x}{a}\int\limits_{0}^{a}f(x) \sin \frac{n\pi x}{a}\,dx. \end{equation*}

Example 7.4.5.

To find the steady state temperature distribution in a thin plate bounded by the lines \(x=0,x=\lambda,y=0,y=\infty\text{,}\) the sides \(x=0,x=\lambda\) are kept at temperature zero, the side \(y=0\) is kept at temperature \(f(x)\) and the edge \(y=\infty\) at temperature zero.

Solution.

The boundary conditions are

\begin{equation*} u(0,y)=0=u(\lambda,y)=u(x,\infty) \end{equation*}

and

\begin{equation*} u(x,0)=f(x). \end{equation*}

The steady state heat equation is given by

\begin{equation} \frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}} =0 \tag{7.4.14} \end{equation}

Let

\begin{equation} u(x,y)=X(x)Y(y) \tag{7.4.15} \end{equation}

be the solution of eqn. (7.4.14). Substituting of eqn. (7.4.15) into eqn. (7.4.14), we get -

\begin{equation*} Y\frac{\partial^{2}X}{\partial x^{2}} +X\frac{\partial^{2}Y}{\partial y^{2}} =0 \end{equation*}

\begin{equation} \frac{1}{X}\frac{\partial^{2}X}{\partial x^{2}} =-\frac{1}{Y}\frac{\partial^{2}Y}{\partial y^{2}} = -p^{2} \quad \text{(say)} \tag{7.4.16} \end{equation}

\begin{equation*} \therefore, X=A\cos px +B\sin px \end{equation*}

and

\begin{equation*} Y=Ce^{py}+De^{-py} \end{equation*}

\begin{equation} \therefore \quad u(x,y) = \left(A\cos px+B\sin px\right)\left(Ce^{py}+De^{-py}\right) \tag{7.4.17} \end{equation}

from boundary condition \(u(x,\infty)=0 \quad \Rightarrow C=0 \) \([ \because \quad e^{-\infty}=0.]\)

\begin{equation} \therefore \quad u(x,y)=\left(A' \cos px+B' \sin px\right)e^{-py} \tag{7.4.18} \end{equation}

from boundary condition \(u(0,y) =0=A' e^{-py} \quad \Rightarrow A' =0 \text{.}\)

\begin{equation} \therefore \quad u(x,y) = B' \sin px e^{-py} \tag{7.4.19} \end{equation}

also,

\begin{equation*} u(\lambda,y) = 0 = B' \sin p\lambda e^{-py} \quad \because B' \neq 0 \end{equation*}

or,

\begin{equation*} \sin p\lambda = 0 =\sin n\pi, \quad \therefore \quad p=\frac{n\pi}{\lambda}, \quad n=1,2,3,\cdots \end{equation*}

Hence,

\begin{equation} u(x,y) = B_{n}\sin\frac{n\pi x}{\lambda}e^{-\frac{n\pi y}{\lambda}}\tag{7.4.20} \end{equation}

again from

\begin{equation*} u(x,0) = B_{n}\sin\frac{n\pi x}{\lambda} =f(x) \end{equation*}

\begin{equation*} \therefore \quad B_{n} = \frac{2}{\lambda}\int\limits_{0}^{\lambda}f(x)\sin\frac{n\pi x}{\lambda}\,dx \end{equation*}

Example 7.4.6.

To find the steady temperature distribution in a thin rectangular plate bounded by the lines \(x=0,x=\lambda, y=0, y=h\) the edges \(x=0, x=\lambda, y=0 \) are kept at temperature zero while the edge \(y=h\) is kept at temp. \(f(x)\text{.}\)

Solution.

The boundary conditions are

\begin{equation*} u(0,y)=0=u(\lambda,y)=u(x,0)\quad u(x,h) =f(x). \end{equation*}

The steady state heat eqn. is

\begin{equation} \frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}} =0 \tag{7.4.21} \end{equation}

The solution of eqn. (7.4.21) is given by

\begin{equation} u(x,y)=\left(A\cos px+B\sin px\right)\left(Ce^{py}+De^{-py}\right) \tag{7.4.22} \end{equation}

Now

\begin{equation*} u(0,y)=0=A\left(Ce^{py}+De^{-py}\right)\quad \Rightarrow A=0 \end{equation*}

also

\begin{equation*} u(\lambda,y) =0=B\sin p\lambda\left(Ce^{py}+De^{-py}\right) \end{equation*}

\(\Rightarrow \sin py =0=\sin n\pi \quad [\because B \neq 0]\)

\begin{equation} \therefore \quad p=\frac{n\pi}{\lambda}, \quad n=1,2,3,\cdots \tag{7.4.23} \end{equation}

or,

\begin{equation} u(x,y)= \left(C_{n}e^{\frac{n\pi y}{\lambda}} +D_{n}e^{-\frac{n\pi y}{\lambda}}\right)\sin\frac{n\pi x}{\lambda} \tag{7.4.24} \end{equation}

again,

\begin{equation*} u(x,0) = 0 = C_{n}+D_{n} \quad \Rightarrow C_{n}=-D_{n} \end{equation*}

Hence,

\begin{equation*} u(x,y) = C_{n}\left(e^{\frac{n\pi y}{\lambda}} -e^{-\frac{n\pi y}{\lambda}}\right)\sin\frac{n\pi x}{\lambda} \end{equation*}

\begin{equation} =2 C_{n}\sin\frac{n\pi x}{\lambda}\sin\frac{n\pi y}{\lambda}\tag{7.4.25} \end{equation}

using the last boundary condition -

\begin{equation*} u(x,h)= 2 C_{n}\sin\frac{n\pi x}{\lambda}\sin\frac{n\pi y}{\lambda} =f(x) \end{equation*}

or,

\begin{equation*} C_{n}\sin\frac{n\pi h}{\lambda} =\frac{2}{\lambda}\int\limits_{0}^{\lambda}\frac{1}{2}f(x) \sin\frac{n\pi x}{\lambda}\,dx. \end{equation*}

Example 7.4.7.

The diameter of a semi - circular plate of radius \(r\) is kept at \(0^{o} C\) and temperature at the semi - circular boundary is at \(T^{o} C\text{.}\) Find the steady state temperature in the plate.

Solution.

The boundary conditions are

\(u=0\text{,}\) when \(\theta=0 \) for \(0 \leq r \lt a\text{,}\)
\(u\) is finite, when \(r \to 0\text{,}\)
\(u=T\text{,}\) when \(r=a\) for \(0 \lt \theta \lt \pi\text{.}\)

The solution of this problem is

\begin{equation*} u=a_{o}\log r \end{equation*}

\begin{equation} +\sum\limits_{n=1}^{\infty}\left(a_{n}\cos n\theta + b_{n}\sin n\theta\right)\left(p_{n}r^{n}+q_{n}r^{-n}\right) +C_{o} \tag{7.4.26} \end{equation}

But \(u\) is finite when \(r \to 0\text{.}\) Eqn. (7.4.26) must not contain terms of \(\log r\) and \(r^{-n}\) and this will be so when \(a_{o}=0 =q_{n}\text{.}\) Thus eqn. (7.4.26) reduces to

\begin{equation} u=\sum\limits_{n=1}^{\infty}\left(L_{n}\cos n\theta + M_{n}\sin n\theta\right)r^{n} +C_{o} \tag{7.4.27} \end{equation}

from condition (i), \(C_{o}=0 \text{.}\) Hence,

\begin{equation*} u=\sum\limits_{n=1}^{\infty}\left(L_{n}\cos n\theta + M_{n}\sin n\theta\right)r^{n} \end{equation*}

from condition (iii),

\begin{equation*} T= \sum\limits_{n=1}^{\infty}\left(L_{n}\cos n\theta + M_{n}\sin n\theta\right)a^{n} \end{equation*}

from which we can find

\begin{equation*} L_{n} = \frac{2}{\pi}\int\limits_{0}^{\pi}\frac{T}{a^{n}} \cos n\theta \,d\theta \quad = \frac{2T}{\pi a^{n}}\int\limits_{0}^{\pi} \cos n\theta \,d\theta =0 \end{equation*}

and

\begin{equation*} M_{n} = \frac{2}{\pi}\int\limits_{0}^{\pi}\frac{T}{a^{n}} \sin n\theta \,d\theta \end{equation*}

\begin{equation*} = \frac{2T}{\pi a^{n}}\int\limits_{0}^{\pi} \sin n\theta \,d\theta = \frac{2T}{n\pi a^{n}}(1-\cos n\pi) \end{equation*}

Hence, the required solution is

\begin{equation*} u= \frac{2T}{n\pi a^{n}}\sum\limits_{n=1}^{\infty}(1-\cos n\pi)r^{n} \sin n\theta. \end{equation*}

Prev Top Next