Subsection 1.1.4 Linear Combination of Vectors
Let \(\vec{v_{1}},\vec{v_{2}},\vec{v_{3}},\cdots,\vec{v_{n}}\) be the vectors of the same order, then a new vector \(\vec{v}\) is said to be the linear combination of these vectors if there exists scalars \(k_{1},k_{2}, k_{3}, \cdots, k_{n}\text{,}\) such that
\begin{equation}
\vec{v} = k_{1}\vec{v_{1}} + k_{2}\vec{v_{2}} + k_{3}\vec{v_{3}} + \cdots + k_{n}\vec{v_{n}}\tag{1.1.5}
\end{equation}
A set of n vectors is said to be linearly dependent, if there exists \(n\) scalars \(k_{1},k_{2}, k_{3}, \cdots, k_{n}\text{,}\) not all zero (i.e. at least one k’s is non - zero), such that
\begin{equation}
k_{1}\vec{v_{1}} + k_{2}\vec{v_{2}} + k_{3}\vec{v_{3}} + \cdots,+ k_{n}\vec{v_{n}} = \vec{O} \tag{1.1.6}
\end{equation}
where \(\vec{O}\) is a null vector. In equation (1.1.6), if all the k’s are zero, then the vectors \(\vec{v_{1}},\vec{v_{2}},\vec{v_{3}},\cdots,\vec{v_{n}}\) are linearly independent. For linearly dependent vectors, suppose \(k_{n}\) be one of the non - zero scalar, then
\begin{equation*}
k_{n}\vec{v_{n}} = - k_{1}\vec{v_{1}} - k_{2}\vec{v_{2}} + k_{3}\vec{v_{3}} + \cdots,+ k_{n-1}\vec{v}_{n-1}
\end{equation*}
\begin{equation*}
\text{or,} \quad \vec{v_{n}} = \lambda_{1}\vec{v_{1}}+\lambda_{2}\vec{v_{2}} + \lambda_{3}\vec{v_{3}} + \cdots\lambda_{n-1}\vec{v_{n-1}}
\end{equation*}
\(\because\) \(\lambda_{i} = -\frac{k_{i}}{k_{n}} \) = linear combination of (n-1) vectors \(\vec{v_{1}}{,}\vec{v_{2}}{,}\vec{v_{3}}{,}\cdots{,} \vec{v}_{n-1}\)
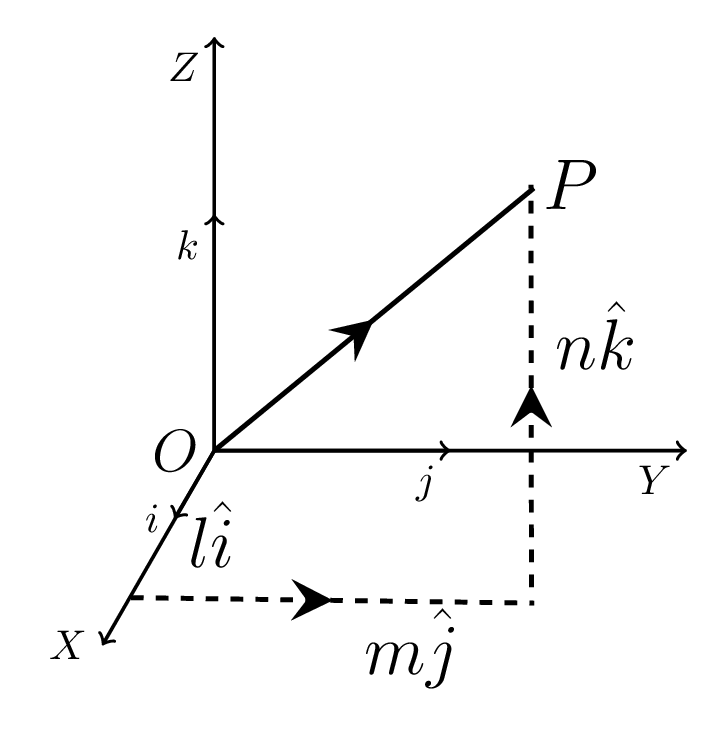
Thus \(n\) vectors are linearly dependent, if any one of them can be expressed as a linear combination of the remaining (n-1) vectors. The vectors \(\vec{v_{1}},\vec{v_{2}},\vec{v_{3}},
\cdots,\vec{v_{n}}\) of equation (1.1.5) form a base or basis for all the vectors in \(n\) - space. Hence these vectors are called the Basis Vectors, i.e., any vectors lying in the given space can be expressed in terms of these basis vectors basis vectors. For example, suppose \(\vec{A}\text{,}\) \(\vec{B}\text{,}\) and \(\vec{C}\) are any three non-zero and non-parallel vectors, and there exists the scalars \(l\text{,}\) \(m\text{,}\) and \(n\) such that \(\vec{D} = l\vec{A}+m\vec{B}+n\vec{C}\text{,}\) then \(\vec{D}\) is a linear combination of vectors\(\vec{A}\text{,}\) \(\vec{B}\text{,}\) and \(\vec{C}\) in three dimensional space. Where \(l\text{,}\) \(m\text{,}\) and \(n\) are components of a \(\vec{D}\) and \(\vec{A}\text{,}\) \(\vec{B}\text{,}\) and \(\vec{C}\) form the basis vectors. In space (or plane) it is advantageous to choose the basis for the vectors as perpendicular vector each of unit length. These vectors are denoted by \(\vec{i}\text{,}\) \(\vec{j}\text{,}\) and \(\vec{k}\) and their common foot by \(O\text{.}\) The lines determined by \(\vec{i}\text{,}\) \(\vec{j}\text{,}\) and \(\vec{k}\) are the \(x\text{,}\) \(y\) and \(z\) axes, respectively. Any vector \(\vec{r}\) in a space with foot at O, as shown in Figure 1.1.4, can be expressed as a linear combination of the basis vectors \(\vec{i}\text{,}\) \(\vec{j}\text{,}\) and \(\vec{k}\text{,}\) such that \(\vec{r}= x\vec{i}+y\vec{j}+z\vec{k}\text{.}\) .
Basis Vectors are a set of linearly independent vectors that span a vector space. A vector space can have many different bases, but any two bases of the same vector space have the same number of vectors, which is known as the dimension of the vector space. For example, in two-dimensional space, the standard basis vectors are (1, 0) and (0, 1), which are perpendicular to each other and span the entire space. Any vector in the plane can be written as a linear combination of these two vectors. Similarly, in three-dimensional space, the standard basis vectors are (1, 0, 0), (0, 1, 0), and (0, 0, 1), which are mutually orthogonal and span the entire space. Any vector in three-dimensional space can be expressed as a linear combination of these three vectors.
