Appendix C Laplace’s equation in cylindrical coordinates
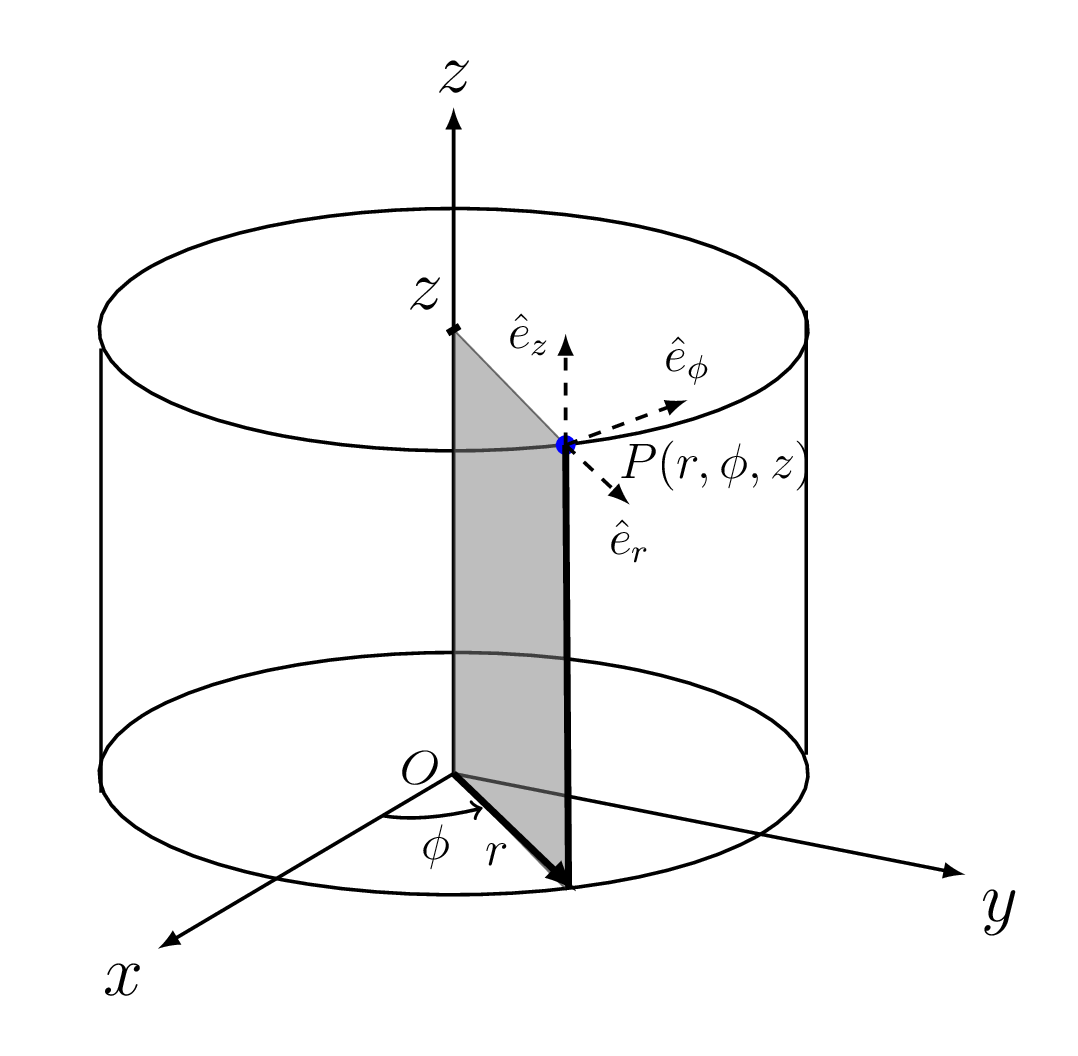
Let us consider the point P having cartesian coordinates \((x,y,z)\) and cylindrical coordinates \((r,\phi,z)\text{,}\) then \(x=r\cos\phi, y=r\sin\phi, z=z, \) so that
\begin{equation*}
r^{2}=x^{2}+y^{2}, \quad \phi =\tan^{-1}(\frac{y}{x}),\quad z=z,
\end{equation*}
and
\begin{equation*}
\frac{\partial r}{\partial x}=\frac{x}{r}=\cos\phi, \quad \frac{\partial r}{\partial y}=\frac{y}{r}=\sin\phi,
\end{equation*}
\begin{equation*}
\frac{\partial \theta}{\partial x}=\frac{1}{1+\frac{y^{2}}{x^{2}}}\left(-\frac{y}{x^{2}}\right)=-\frac{y}{x^{2}+y^{2}} =-\frac{r\sin\phi}{r^{2}}=-\frac{\sin\phi}{r},
\end{equation*}
\begin{equation*}
\frac{\partial \phi}{\partial y} = \frac{1}{1+\frac{y^{2}}{x^{2}}}\left(\frac{1}{x}\right)=\frac{x}{x^{2}+y^{2}} =\frac{r\cos\phi}{r^{2}}=\frac{\cos\phi}{r},
\end{equation*}
Now,
\begin{equation*}
\frac{\partial u}{\partial x}= \frac{\partial u}{\partial r} \frac{\partial r}{\partial x}+\frac{\partial u}{\partial \phi}\frac{\partial \phi}{\partial x}
\end{equation*}
\begin{equation*}
= \frac{\partial u}{\partial r} \cos\phi +\frac{\partial u}{\partial \phi}\left(-\frac{\sin\phi}{r}\right)
\end{equation*}
\begin{equation}
=\cos\phi \frac{\partial u}{\partial r}-\frac{\sin\phi}{r}\frac{\partial u}{\partial \phi} \tag{C.0.1}
\end{equation}
so the operator
\begin{equation*}
\frac{\partial }{\partial x} \equiv \cos\phi \frac{\partial }{\partial r} -\frac{\sin\phi}{r}\frac{\partial }{\partial \phi}
\end{equation*}
and
\begin{equation*}
\frac{\partial^{2} u}{\partial x^{2}} =\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}\right)
\end{equation*}
\begin{equation*}
= \left(\cos\phi \frac{\partial }{\partial r} -\frac{\sin\phi}{r}\frac{\partial }{\partial \phi}\right)\left(\cos\phi \frac{\partial u}{\partial r} -\frac{\sin\phi}{r}\frac{\partial u}{\partial \phi}\right)
\end{equation*}
\begin{equation*}
=\cos^{2}\phi \frac{\partial^{2} u}{\partial r^{2}} +\frac{2\cos\phi\sin\phi}{r^{2}}\frac{\partial u}{\partial \phi}-\frac{2\cos\phi\sin\phi}{r}\frac{\partial^{2} u}{\partial r\partial \phi}
\end{equation*}
\begin{equation}
+\frac{\sin^{2}\phi}{r}\frac{\partial u}{\partial r}+\frac{\sin^{2}\phi}{r^{2}}\frac{\partial^{2} u}{\partial \phi^{2}} \tag{C.0.2}
\end{equation}
or,
\begin{equation*}
\frac{\partial u}{\partial y} =\frac{\partial u}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial u}{\partial \phi}\frac{\partial \phi}{\partial y} = \sin\phi\frac{\partial u}{\partial r}+\frac{\cos\phi}{r}\frac{\partial u}{\partial \phi}
\end{equation*}
and
\begin{equation*}
\frac{\partial }{\partial y} \equiv \sin\phi\frac{\partial }{\partial r}+\frac{\cos\phi}{r}\frac{\partial }{\partial \phi}
\end{equation*}
\begin{equation*}
\therefore \frac{\partial^{2} u}{\partial y^{2}} =\sin^{2}\phi\frac{\partial^{2} u}{\partial r^{2}}-\frac{2\sin\phi\cos\phi}{r^{2}}\frac{\partial u}{\partial \phi}
\end{equation*}
\begin{equation*}
+\frac{2\sin\phi\cos\phi}{r}\frac{\partial^{2} u}{\partial r\partial \phi}
\end{equation*}
\begin{equation}
+\frac{\cos^{2}\phi}{r}\frac{\partial u}{\partial r}+\frac{\cos^{2}\phi}{r^{2}}\frac{\partial^{2} u}{\partial \phi^{2}} \tag{C.0.3}
\end{equation}
and
\begin{equation}
\frac{\partial^{2} u}{\partial z^{2}} =\frac{\partial^{2} u}{\partial z^{2}} \tag{C.0.4}
\end{equation}
\begin{equation*}
\frac{\partial^{2} u}{\partial x^{2}} +\frac{\partial^{2} u}{\partial y^{2}} +\frac{\partial^{2} u}{\partial z^{2}} =\frac{\partial^{2} u}{\partial r^{2}} +\frac{1}{r}\frac{\partial u}{\partial r} +\frac{1}{r^{2}}\frac{\partial^{2} u}{\partial \phi^{2}}+\frac{\partial^{2} u}{\partial z^{2}}
\end{equation*}
Hence, Laplace’s differential equation in cylindrical coordinates is
\begin{equation*}
\frac{\partial^{2} u}{\partial r^{2}} +\frac{1}{r}\frac{\partial u}{\partial r} +\frac{1}{r^{2}}\frac{\partial^{2} u}{\partial \phi^{2}}+\frac{\partial^{2} u}{\partial z^{2}} =0
\end{equation*}
and
\begin{equation*}
\frac{1}{r} \frac{\partial}{\partial r}\left(r\frac{\partial u}{\partial r}\right)+\frac{1}{r^{2}}\frac{\partial^{2} u}{\partial \phi^{2}}+\frac{\partial^{2} u}{\partial z^{2}} =0
\end{equation*}
