Mathematical Methods of Physics: For Undergraduate

\begin{equation*} \vec{F}=2x^{2}.4x^{2}\hat{i}+3x.4x^{2}\hat{j}=8x^{4}\hat{i}+12x^{3}\hat{j} \end{equation*}

\begin{equation*} \vec{r}=x\hat{i}+y\hat{j}= x\hat{i}+4x^{2}\hat{j} \end{equation*}

\begin{equation*} \vec{\,dr} = \,dx\hat{i}+8x\,dx\hat{j} \end{equation*}

\begin{equation*} \therefore \text{Work done} \quad \int_{c}\vec{F}\cdot\vec{\,dr} = \int^{1}_{0} (8x^{4}\hat{i}+ 12x^{3}\hat{j}) \cdot (dx\hat{i}+8x\,dx\hat{j}) \end{equation*}

\begin{equation*} =\int^{1}_{0} (8x^{4}dx+ 96x^{4}dx)=\int^{1}_{0} 104x^{4}\,dx \end{equation*}

\begin{equation*} = 104\int^{1}_{0}x^{4}\,dx = 104\left[x^{5}/5\right]^{1}_{0}=104/5. \end{equation*}

\begin{equation*} \int_{c}\vec{F}\cdot\vec{\,dr} =\int_{c}\left(\frac{\hat{i}y-\hat{j}x}{x^{2}+y^{2}}\right)\cdot (\,dx\hat{i}+\,dy\hat{j}+\,dz\hat{k}) \end{equation*}

\begin{equation*} =\int_{c}\left(\frac{y\,dx-x\,dy}{x^{2}+y^{2}}\right) = \int_{c}\left({y\,dx-x\,dy}\right) \end{equation*}

\begin{align*} x\amp = 1 \cos\theta\\ y\amp =1 \sin\theta \end{align*}

\begin{equation*} \therefore \,dx= -\sin\theta \,d\theta, \,dy=\cos\theta \,d\theta \end{equation*}

\begin{equation*} \int\limits_{c}\vec{F}\cdot\vec{dr} =\int\limits_{0}^{2\pi} \left[\sin\theta(-\sin\theta \,d\theta)-\cos\theta (\cos\theta \,d\theta)\right] \end{equation*}

\begin{equation*} =-\int\limits_{0}^{2\pi}( \sin^{2}\theta+\cos^{2}\theta)\,d\theta =-\int\limits_{0}^{2\pi} \,d\theta=-\left(\theta\right)_{0}^{2\pi}=-2\pi. \end{equation*}

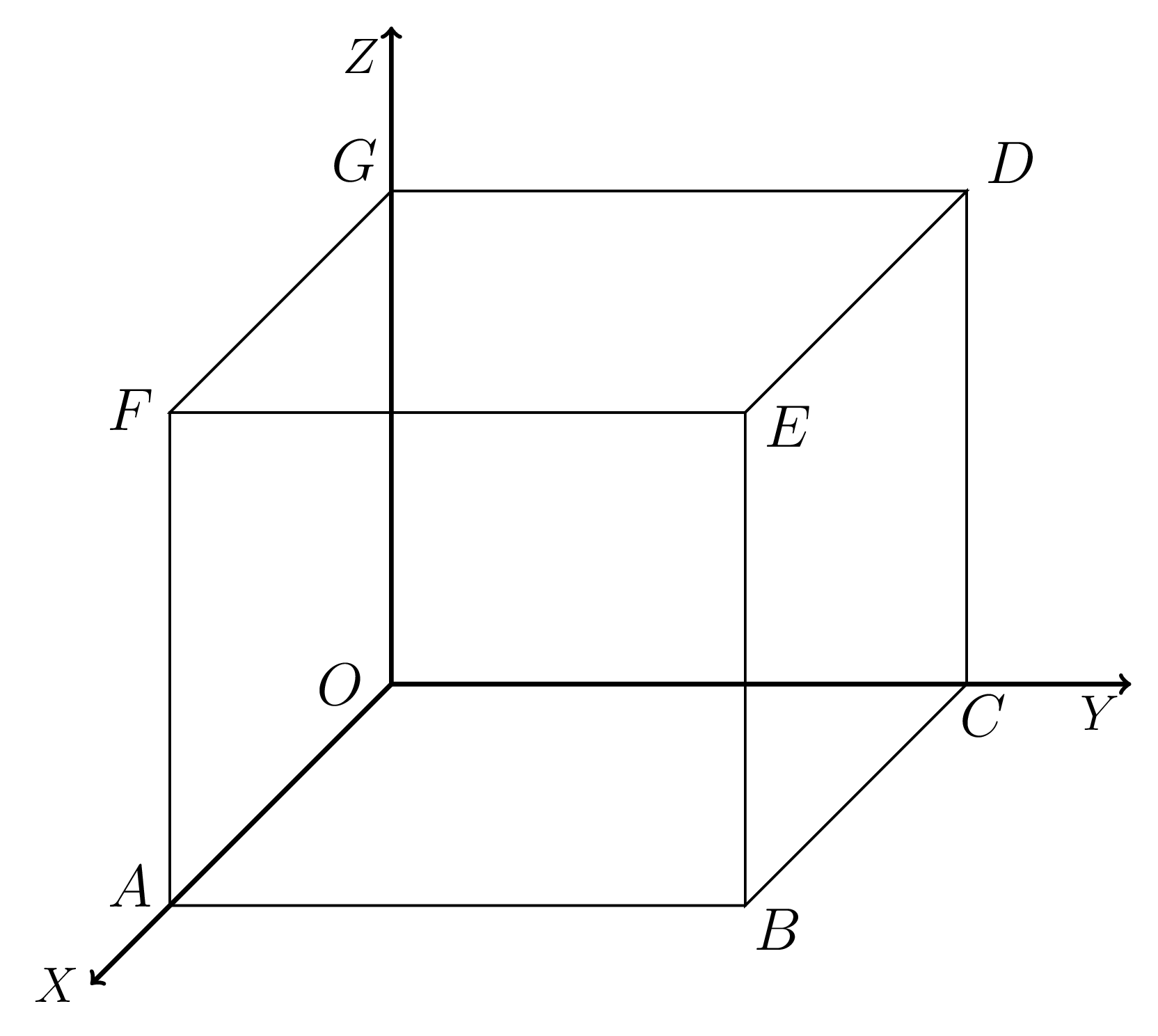
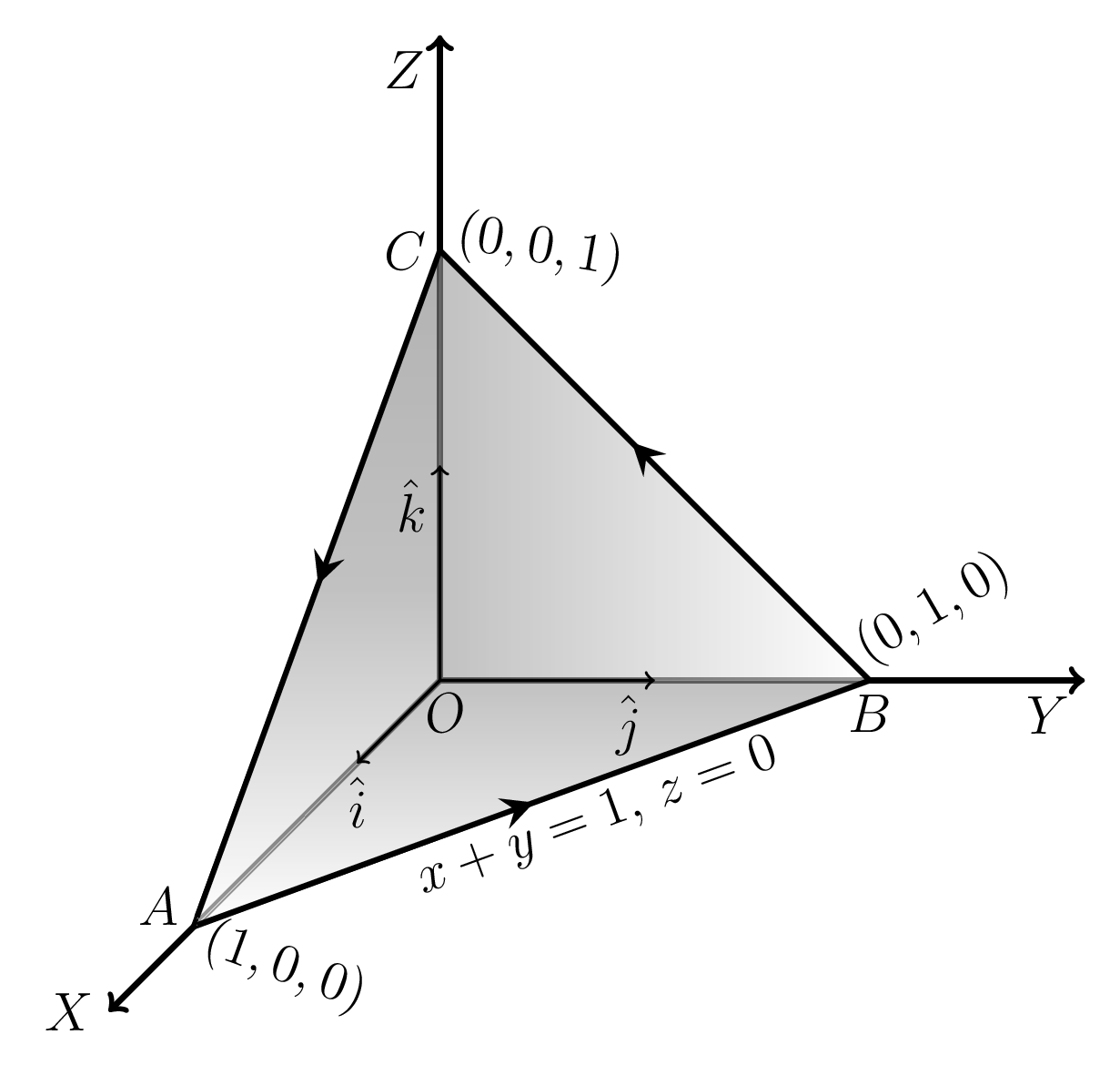
\begin{equation*} \iint\limits_{S}\vec{F}\cdot \hat{n}\,ds= \iint\limits_{OABC}\vec{F}\cdot \hat{n}\,ds+\iint\limits_{DEFG}\vec{F}\cdot \hat{n}\,ds \end{equation*}

\begin{equation*} \quad +\iint\limits_{OAFG}\vec{F}\cdot \hat{n}\,ds +\iint\limits_{BCDE}\vec{F}\cdot \hat{n}\,ds \end{equation*}

\begin{equation} \qquad +\iint\limits_{ABEF}\vec{F}\cdot \hat{n}\,ds+\iint\limits_{OCDG}\vec{F}\cdot \hat{n}\,ds \tag{1.5.1} \end{equation}

\begin{equation*} Now,\quad \iint\limits_{OABC}\vec{F}\cdot \hat{n}\,ds= \iint\limits_{OABC}(4xz\hat{i}-y^{2}\hat{j}+yz\hat{k})\cdot (-\hat{k})\,dx\,dy \end{equation*}

\begin{equation*} \quad =-\int\limits_{0}^{1}\int\limits_{0}^{1}yz\,dx\,dy=0.\quad [\because z=0 \quad\text{for face OABC}] \end{equation*}

\begin{equation*} \iint\limits_{DEFG}\vec{F}\cdot \hat{n}\,ds= \iint\limits_{DEFG}(4xz\hat{i}-y^{2}\hat{j}+yz\hat{k})\cdot (\hat{k})\,dx\,dy \end{equation*}

\begin{equation*} =\int\limits_{0}^{1}\int\limits_{0}^{1}yz\,dx\,dy =\int\limits_{0}^{1}\int\limits_{0}^{1}y.1 \,dx\,dy = \int\limits_{0}^{1}\,dx\int\limits_{0}^{1}y\,dy \end{equation*}

\begin{equation*} = \int\limits_{0}^{1}\,dx\left(\frac{y^{2}}{2}\right)_{0}^{1} =\frac{1}{2}(x)^{1}_{0}=\frac{1}{2}. \hspace{3pt} \text{(as z=1)} \end{equation*}

\begin{equation*} \iint\limits_{OAFG}\vec{F}\cdot \hat{n}\,ds = \iint\limits_{OAFG}(4xz\hat{i}-y^{2}\hat{j}+yz\hat{k})\cdot (-\hat{j})\,dx\,dz \end{equation*}

\begin{equation*} =\int\limits_{0}^{1}\int\limits_{0}^{1}y^{2}\,dx\,dz=0. \quad \text{(as y = 0)} \end{equation*}

\begin{equation*} \iint\limits_{BCDE}\vec{F}\cdot \hat{n}\,ds = \iint\limits_{BCDE}(4xz\hat{i}-y^{2}\hat{j}+yz\hat{k})\cdot (\hat{j})\,dx\,dz=\int\limits_{0}^{1}\int\limits_{0}^{1}-y^{2}\,dx\,dz \end{equation*}

\begin{equation*} =-\int\limits_{0}^{1}\int\limits_{0}^{1} dxdz = -\int\limits_{0}^{1}\,dx\int\limits_{0}^{1}\,dz = -\left(x\right)^{1}_{0}\left(z\right)^{1}_{0}=-1. \hspace{3pt} \text{(as y=1)} \end{equation*}

\begin{equation*} \iint\limits_{ABEF}\vec{F}\cdot \hat{n}\,ds= \iint\limits_{ABEF}(4xz\hat{i}-y^{2}\hat{j}+yz\hat{k})\cdot (\hat{i})\,dy\,dz=\int\limits_{0}^{1}\int\limits_{0}^{1}(4xz\,dy\,dz \end{equation*}

\begin{equation*} =\int\limits_{0}^{1}\int\limits_{0}^{1} 4.1.z \,dy\,dz = 2. \quad \text{(as x=1)} \end{equation*}

\begin{equation*} \iint\limits_{OCDG}\vec{F}\cdot \hat{n}\,ds= \iint\limits_{OCDG}(4xz\hat{i}-y^{2}\hat{j}+yz\hat{k})\cdot (-\hat{i})\,dy\,dz \end{equation*}

\begin{equation*} =-\int\limits_{0}^{1}\int\limits_{0}^{1}(4xz\,dy\,dz= 0. \quad \text{(as x=0)} \end{equation*}

\begin{equation*} \iint\limits_{S}\vec{F}\cdot \hat{n}\,ds = 0+\frac{1}{2}+0-1+2+0=\frac{3}{2}. \hspace{3pt} proved. \end{equation*}

\begin{equation} \iint\limits_{S}\vec{F}\cdot \hat{n}ds=\iint\limits_{R}\vec{F}\cdot \hat{n}\frac{dxdy}{\mid \hat{n}\cdot\hat{k}\mid}\tag{1.5.2} \end{equation}

\begin{equation*} \hat{n}=\frac{\text{grad f} }{\mid \text{grad f} \mid} \end{equation*}

\begin{equation*} \text{grad} f=\vec{\nabla}f = \vec{\nabla}(2x+3y+6z-12)=2\hat{i}+3\hat{j}+6\hat{k} \end{equation*}

\begin{equation*} \mid \text{grad} f\mid =\sqrt{4+9+36} =\sqrt{49} = 7. \end{equation*}

\begin{equation*} \therefore \hat{n}=\frac{2\hat{i}+3\hat{j}+6\hat{k}}{7} \end{equation*}

\begin{equation*} \hat{n}\cdot\hat{k} = \frac{1}{7}(2\hat{i}+3\hat{j}+6\hat{k})\cdot\hat{k}=\frac{6}{7} \end{equation*}

\begin{equation*} \vec{F}\cdot\hat{n}=(18z\hat{i}-12\hat{j}+3y\hat{k})\cdot \frac{1}{7}(2\hat{i}+3\hat{j}+6\hat{k}) = \frac{36z-36+18y}{7}, \end{equation*}

\begin{equation*} z=\frac{12-2x-3y}{6} \end{equation*}

\begin{equation*} \therefore \vec{F}\cdot\hat{n}=\frac{1}{7}\left[36\left(\frac{12-2x-3y}{6}\right)-36+18y\right] \end{equation*}

\begin{equation*} = \frac{1}{7}(72-12x-18y-36+18y) = \frac{1}{7}(36-12x). \end{equation*}

\begin{equation*} \iint\limits_{S}\vec{F}\cdot \hat{n}ds=\iint\limits_{R}\vec{F}\cdot \hat{n}\frac{dxdy}{\mid \hat{n}\cdot\hat{k}\mid} =\iint\limits_{R} \frac{1}{7}(36-12x)\frac{dxdy}{6}\cdot7 \end{equation*}

\begin{equation*} = \iint\limits_{R} (6-2x) \,dx\,dy \end{equation*}

\begin{equation*} \therefore \quad \iint\limits_{S}\vec{F}\cdot \hat{n}\,ds =\int\limits_{x=0}^{6}\int\limits_{y=0}^{(12-2x)/3}(6-2x)\,dx\,dy \end{equation*}

\begin{equation*} =\int\limits_{x=0}^{6}(6-2x)dx[y]^{(12-2x)/3}_{3} = \int\limits_{x=0}^{6}(24-12x+\frac{4}{3}x^{2})dx \end{equation*}

\begin{equation*} =24. \end{equation*}

\begin{equation*} \iint\limits_{S}\vec{F}\cdot \hat{n}ds=\iint\limits_{R}\vec{F}\cdot \hat{n}\frac{dxdz}{\mid \hat{n}\cdot\hat{j}\mid} \end{equation*}

\begin{equation*} \hat{n}=\frac{grad f}{\mid grad f\mid}= \frac{\vec{\nabla f}}{\mid\vec{\nabla f}\mid} =\frac{\vec{\nabla}(x^{2}+y^{2}-16)}{\mid\vec{\nabla}(x^{2}+y^{2}-16)\mid} \end{equation*}

\begin{equation*} =\frac{(2x\hat{i}+2y\hat{j})}{\sqrt{(4x^{2}+4y^{2})}} =\frac{(x\hat{i}+y\hat{j})}{\sqrt{(x^{2}+y^{2})}} =\frac{(x\hat{i}+y\hat{j})}{4}, \end{equation*}

\begin{equation*} \vec{F}\cdot\hat{n}=(z\hat{i}-x\hat{j}+3y^{2}z\hat{k}).\frac{1}{4}(x\hat{i}+y\hat{j}) = \frac{1}{4}(xz+xy), \end{equation*}

\begin{equation*} \hat{n}\cdot\hat{j}= \frac{1}{4}(x\hat{i}+y\hat{j})\cdot\hat{j}=\frac{1}{4}y \end{equation*}

\begin{equation*} \therefore \iint\limits_{R}\vec{F}\cdot \hat{n}\frac{dxdz}{\mid \hat{n}\cdot\hat{j}\mid} =\iint\limits_{R}\frac{1}{4}(xz+xy)\cdot\frac{4}{y}\,dx\,dz \end{equation*}

\begin{equation*} =\iint\limits_{R}\left(\frac{xz}{\sqrt{(16-x^{2})}}+x\right)\,dx\,dz \end{equation*}

\begin{equation*} = \int\limits_{x=0}^{4}\int\limits_{z=0}^{5}\left(\frac{xz}{\sqrt{(16-x^{2})}}+x\right)dxdz = \int\limits_{z=0}^{5}(4z+8)dz=90. \end{equation*}

\begin{equation*} \iiint\limits_{V}\vec{F}dv=\iiint\limits_{V}(2z\hat{i}-x\hat{j}+y\hat{k})\,dx\,dy\,dz \end{equation*}

\begin{equation*} =\int\limits_{x=0}^{2}\int\limits_{y=0}^{4}\int\limits_{z=x^{2}}^{2}(2z\hat{i}-x\hat{j}+y\hat{k})\,dx\,dy\,dz \end{equation*}

\begin{equation*} =\int\limits_{0}^{2}dx\int\limits_{0}^{4}dy[z^{2}\hat{i}-xz\hat{j}+yz\hat{k}]^{2}_{x^{2}} \end{equation*}

\begin{equation*} =\int\limits_{0}^{2}dx\int\limits_{0}^{4}dy[4\hat{i}-2x\hat{j}+2yz\hat{k}-x^{4}\hat{i}+x^{3}\hat{j}-x^{2}y\hat{k}] \end{equation*}

\begin{equation*} = \int\limits_{0}^{2}dx\left[4y\hat{i}-2xy\hat{j}+y^{2}\hat{k}-x^{4}y\hat{i}+x^{3}y\hat{j}-\frac{x^{2}y^{2}}{2}\hat{k}\right]^{4}_{0} \end{equation*}

\begin{equation*} = \int\limits_{0}^{2}(16\hat{i}-8x\hat{j}+16\hat{k}-4x^{4}\hat{i}+4x^{3}\hat{j}-8x^{2}\hat{k})\,dx \end{equation*}

\begin{equation*} = \left[16x\hat{i}-4x^{2}\hat{j}+16\hat{k}-\frac{4}{5}x^{5}\hat{i}+x^{4}\hat{j}-\frac{8}{3}x^{3}\hat{k}\right]^{2}_{0} \end{equation*}

\begin{equation*} =32\hat{i}-16\hat{j}+32\hat{k}-\frac{128}{5}\hat{i}+16\hat{j}-\frac{64}{3}\hat{k} \end{equation*}

\begin{equation*} =\frac{32}{5}\hat{i}+32\hat{k}=\frac{32}{5}(3\hat{i}+5\hat{k}). \end{equation*}

\begin{equation*} \iiint\limits_{V}\phi dV=\iiint\limits_{V}45x^{2}y \,dx\,dy\,dz. \end{equation*}

\begin{equation*} \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} \vec{E}\cdot\vec{\,dS}= \iiint\limits_{V}(\vec{\nabla}\cdot \vec{E})\,dV=\iiint\limits_{V}\left[\frac{\delta E_{x}}{\delta x}+\frac{\delta E_{y}}{\delta y}+\frac{\delta E_{z}}{\delta z}\right] \,dV \end{equation*}

\begin{equation} \therefore \quad \mathop{\vcenter{\huge\unicode{x222F}\,}}_{S} \vec{E}\cdot\vec{\,dS} = \iiint\limits_{V} a \,dV = aV=aL^{3} \tag{1.5.3} \end{equation}

\begin{equation} \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} \vec{E}\cdot\vec{\,dS} = \frac{q}{\epsilon_{o}} \tag{1.5.4} \end{equation}

\begin{equation*} \frac{q}{\epsilon_{o}} = aL^{3}. \end{equation*}

\begin{equation*} \therefore \quad q = \epsilon_{o} a L^{3}. \end{equation*}

\begin{equation*} \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} \vec{A}\cdot\vec{dS}=\iiint\limits_{V} div\vec{A} \,dV \end{equation*}

\begin{equation*} = \iiint\limits_{V} \left(\hat{i}\frac{\partial}{\partial x}+\hat{j}\frac{\partial}{\partial y} +\hat{k}\frac{\partial}{\partial z}\right)\cdot (x^{3}\hat{i}+ y^{3}\hat{j}+z^{3}\hat{k})\,dV \end{equation*}

\begin{equation*} =\iiint\limits_{V} \left(3x^{2}+ 3y^{2}+3z^{2}\right)dV= 3\iiint\limits_{V} \left(x^{2}+ y^{2}+z^{2}\right)\,dV =3\iiint\limits_{V}a^{2}dV= 3a^{2}\iiint\limits_{V}\,dV = 3a^{2}\left(\frac{4}{3}\pi a^{3}\right) = 4\pi a^{5}. \end{equation*}

\begin{equation*} \iint\limits_{S} \vec{F}\cdot\hat{n}\,dS = \iiint\limits_{V} div\vec{F} \,dV \end{equation*}

\begin{equation*} =\iiint\limits_{V} \left(\hat{i}\frac{\partial}{\partial x}+\hat{j}\frac{\partial}{\partial y}+\hat{k}\frac{\partial}{\partial z}\right)\cdot (x^{2}+ y^{2}+z^{2})(\hat{i}+\hat{j}+\hat{k})\,dV \end{equation*}

\begin{equation*} =\iiint\limits_{V} \left(2x+2y+2z\right)\,dV =2\iiint\limits_{V} \left(x+y+z\right)\,dV = 2\iiint\limits_{V}2\,dV \end{equation*}

\begin{equation*} = 4 \text{[volume of tetrahedron OABC]} \end{equation*}

\begin{equation*} = 4[\frac{1}{3} \text{Area of the base}\hspace{2pt} OAB \times \text{height}\hspace{2pt} OC] \end{equation*}

\begin{equation*} = 4[\frac{1}{3}(\frac{1}{2}\times 2 \times 2)\times 2] = \frac{16}{3}. \end{equation*}

\begin{equation*} \int\limits_{C}\left[(2x-y)\,dx-yz^{2}\,dy-y^{2}z\,dz\right] \end{equation*}

\begin{equation*} =\int\limits_{C}\left[(2x-y)\hat{i}-yz^{2}\hat{j}-y^{2}z\hat{k}\right]\cdot(\hat{i}dx+\hat{j}dy+\hat{k}\,dz) =\int\limits_{C}\vec{F}\cdot\vec{\,dr} \end{equation*}

\begin{equation} \int\limits_{C}\vec{F}\cdot\vec{dr}=\iint\limits_{S}curl\vec{F}\cdot\hat{n}ds \tag{1.5.5} \end{equation}

\begin{equation*} \therefore \quad curl\vec{F}=\vec{\nabla}\times\vec{F}= {\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\2x-y & -yz^{2} & -y^{2}z \end{vmatrix}} \end{equation*}

\begin{equation*} \int\limits_{C}\vec{F}\cdot\vec{\,dr}=\iint\limits_{S}\hat{k}\cdot\hat{n}\,ds=\iint\limits_{S}\,dx\,dy \end{equation*}

\begin{equation*} =\int\limits_{-1}^{+1}\,dx\int\limits_{-\sqrt{1-x^{2}}}^{+\sqrt{1-x^{2}}}\,dy=\int\limits_{-1}^{+1}[\sqrt{1-x^{2}}+\sqrt{1-x^{2}}] \,dx \end{equation*}

\begin{equation*} =2\int\limits_{-1}^{+1}[\sqrt{1-x^{2}}]dx =2\left[\frac{x}{2} \sqrt{1-x^{2}}+\frac{1}{2} sin^{-1}x\right]^{+1}_{-1} \end{equation*}

\begin{equation*} =2\left[0+\frac{1}{2} (\frac{\pi}{2})-\frac{1}{2} (\frac{-\pi}{2})\right] = \pi. \end{equation*}

\begin{equation*} \iint\limits_{S}curl\vec{V}\cdot\hat{n}ds = \int\limits_{c}\vec{V}\cdot\vec{\,dr} =\int\limits_{c}(\hat{i}y+\hat{j}z+\hat{k}x)\cdot(\,dx\hat{i}+\,dy\hat{j}+\,dz\hat{k}) \end{equation*}

\begin{equation*} =\int\limits_{C}(y\,dx+z\,dy)= \int\limits_{C}y\,dx \quad [\because z=0] \end{equation*}

\begin{equation*} \therefore \iint\limits_{S}curl\vec{V}\cdot\hat{n}\,ds= \int\limits_{0}^{2\pi}\sin\theta.(-\sin\theta)\,d\theta = \int\limits_{0}^{2\pi}\sin^{2}\theta \,d\theta \end{equation*}

\begin{equation*} =\frac{1}{2}\int\limits_{0}^{2\pi}(\cos 2\theta -1) \,d\theta =\frac{1}{2}\left(\frac{\sin2\theta}{2}-\theta\right)^{2\pi}_{0} = -\pi. \end{equation*}

\begin{equation*} \int\limits_{C}\vec{F}\cdot\vec{\,dr}=\int\limits_{C}[(2y+z)\hat{i}+(x-z)\hat{j}+(y-x)\hat{k}]\cdot (\,dx\hat{i}+\,dy\hat{j}+\,dz\hat{k}) \end{equation*}

\begin{equation*} =\int\limits_{C}[(2y+z)\,dx+(x-z)\,dy+(y-x)\,dz]. \end{equation*}

\begin{equation} \int\limits_{C}\vec{F}\cdot\vec{\,dr}=\int\limits_{AB}\vec{F}\cdot\vec{\,dr}+\int\limits_{BC}\vec{F}\cdot\vec{\,dr}+\int\limits_{CA}\vec{F}\cdot\vec{\,dr}. \tag{1.5.6} \end{equation}

\begin{equation*} \int\limits_{AB}\vec{F}\cdot\vec{\,dr}= \int\limits_{A}^{B}(2y\,dx+x\,dy) = \int\limits_{1}^{0}2(1-x)\,dx+\int\limits_{0}^{1}(1-y)\,dy \end{equation*}

\begin{equation*} =2\left(x-\frac{x^{2}}{2}\right)^{0}_{1}+\left(y-\frac{y^{2}}{2}\right)^{1}_{0}=-\frac{1}{2}. \end{equation*}

\begin{equation*} \int\limits_{BC}\vec{F}\cdot\vec{\,dr}= \int\limits_{B}^{C}(-z\,dy+y\,dz) = \int\limits_{1}^{0}(1-y)\,dy+\int\limits_{0}^{1}(1-z)\,dz \end{equation*}

\begin{equation*} =-\left(y-\frac{y^{2}}{2}\right)^{0}_{1}+\left(z-\frac{z^{2}}{2}\right)^{1}_{0}=1. \end{equation*}

\begin{equation*} \int\limits_{CA}\vec{F}\cdot\vec{\,dr}= \int\limits_{C}^{A}(z\,dx-x\,dz)= \int\limits_{0}^{1}(1-x)\,dx-\int\limits_{1}^{0}(1-z)\,dz \end{equation*}

\begin{equation*} =\left(x-\frac{x^{2}}{2}\right)^{1}_{0}-\left(z-\frac{z^{2}}{2}\right)^{0}_{1}=1. \end{equation*}

\begin{equation} \int\limits_{C}\vec{F}\cdot\vec{\,dr}=-\frac{1}{2}+1+1=\frac{3}{2}. \tag{1.5.7} \end{equation}

\begin{equation*} {\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\2y+z & x-z & y-x \end{vmatrix}} \end{equation*}

\begin{equation*} = \hat{i}(1+1)-\hat{j}(-1-1)+\hat{k}(1-2) = 2\hat{i}+2\hat{j}-\hat{k}. \end{equation*}

\begin{equation*} \iint\limits_{S}\left(\vec{\nabla}\times\vec{F}\right)\cdot\hat{n}ds=\iint\limits_{S}(2\hat{i}+2\hat{j}-\hat{k})\cdot\hat{k}\frac{1}{2}\,dx\,dy \end{equation*}

\begin{equation*} =\int\limits_{0}^{1}\int\limits_{0}^{1}(-\frac{1}{2})\,dx\,dy= -\frac{1}{2}[x]^{1}_{0}[y]^{1}_{0}=-\frac{1}{2} \end{equation*}

\begin{equation*} \iint\limits_{S}\left(\vec{\nabla}\times\vec{F}\right)\cdot\hat{n}\,ds=\iint\limits_{S}(2\hat{i}+2\hat{j}-\hat{k})\cdot\hat{i}(\frac{1}{2})\,dy\,dz \end{equation*}

\begin{equation*} =\int\limits_{0}^{1}\int\limits_{0}^{1}(2.\frac{1}{2})\,dy\,dz= 1. \end{equation*}

\begin{equation*} \iint\limits_{S}\left(\vec{\nabla}\times\vec{F}\right)\cdot\hat{n}\,ds=\iint\limits_{S}(2\hat{i}+2\hat{j}-\hat{k})\cdot\hat{j}(\frac{1}{2})\,dx\,dz \end{equation*}

\begin{equation*} =\int\limits_{0}^{1}\int\limits_{0}^{1}(2.\frac{1}{2})\,dx\,dz= 1. \end{equation*}

\begin{equation} \iint\limits_{S}\left(\vec{\nabla}\times\vec{F}\right)\cdot\hat{n}\,ds =-\frac{1}{2}+1+1=\frac{3}{2}. \tag{1.5.8} \end{equation}