Subsection 5.5.3 Gibb’s Phenomenon
Gibb’s phenomenon describes a special case where a funciton has a jump discontinuity. An anomaly occurs near the discontinuity in an approximation of an original function using its Fourier series. The values of the partial sums near the discontinuity overshoot or undershoot the fuction value. As more and more terms incorporate in the partial sums the graph of the function resembles the original function more closely away from the point of discontinuity. However, the blips near the discontinuity persists. Although the size of blips decreases in width they appear to remain at the same height. In other words, the series converges correctly at any point due to increase of terms in the partial sums, but the blips do not converges to zero as shown in figure Figure 5.5.1. This lack of improvement in the approximation near the discontinuity menifested in the continual presence of the overshoot or undershoot is the Gibb’s phenomenon.
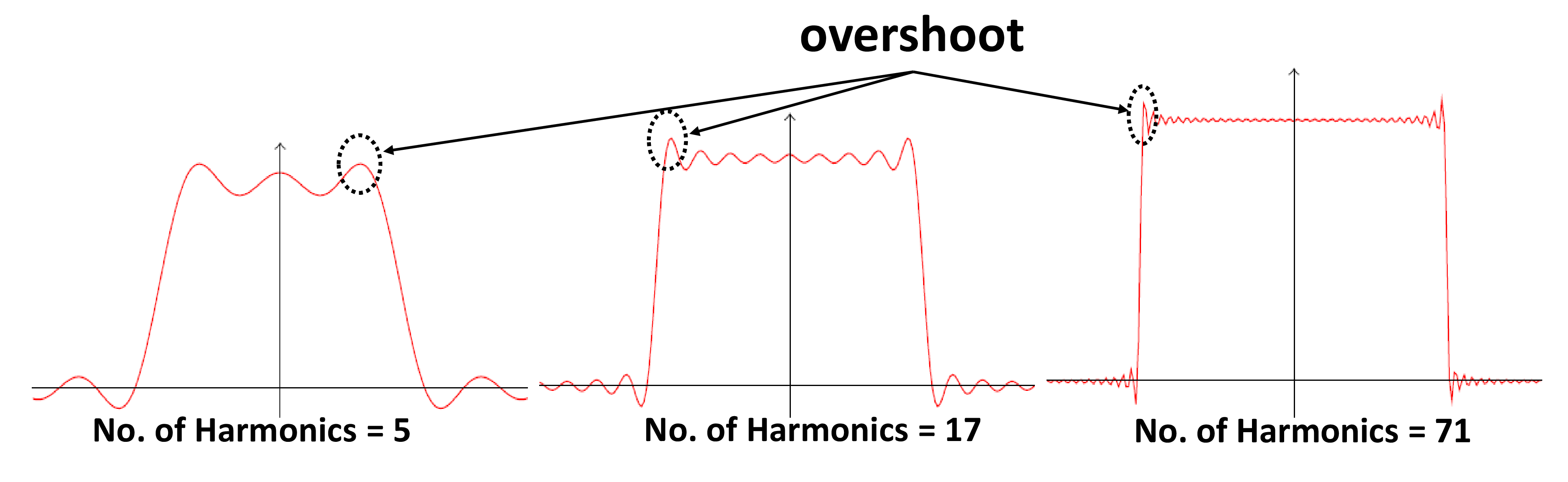
In the immediate vicinity of a jump discontinuity i.e. at \(x{+}\) or \(x{-}\text{,}\) the function \(f(x)\) is not same and hence the convergence of the Fourier series is not uniform since \(f(x) \rightarrow \frac{1}{2}[f(x+0)+f(x-0)]\text{.}\) Here partial sums move progressively closer to the function as the number of terms is increased, but the partial sums (approximating curves) overshoot or undershoot the function at the jump discontinuity. To verify the validity of Gibbs phenomenon, i.e. Fourier expansion for functions which are discontinuous but piecewise smooth, Bocher considered the following specific function defined by
\begin{equation}
f(x) = \frac{1}{2}(\pi-x) \quad (0\leq x \leq 2\pi)\tag{5.5.7}
\end{equation}
here \(f(0) = 0\) and \(f(x+2\pi) =f(x)\text{.}\) i.e., the function jumps by \(\pi\) at the points \(x = \pm 2m\pi\) where \(m=0,1,2,\cdots\text{.}\) The Fourier coefficients of this function are \(a_{0}=a_{n}=0, \quad b_{n}=\frac{1}{n}\text{.}\)
Thus, if the Fourier expansion for such functions is valid, we have
\begin{equation}
s(x)=\displaystyle{\lim_{p \to \infty}} s_{p}(x) = \sum\limits_{n=1}^{\infty}\frac{\sin nx}{n}\tag{5.5.8}
\end{equation}
The partial sum is given by
\begin{equation*}
s_{p}(x) = \sum\limits_{n=1}^{p}\frac{\sin nx}{n} = \sin x +\frac{1}{2}\sin 2x +\cdots+\frac{1}{p}\sin px
\end{equation*}
\begin{equation*}
=\int\limits_{0}^{x}(\cos u +\cos 2u + \cdots + \cos pu)\,du =\int\limits_{0}^{x}\left(\sum\limits_{n=1}^{p}\cos nu\right)\,du
\end{equation*}
\begin{equation*}
=\frac{1}{2} \int\limits_{0}^{x}\frac{\sin\left[\left(p+\frac{1}{2}\right)u\right]}{\sin u/2}\,du -\frac{x}{2}
\end{equation*}
\begin{equation*}
\left[\because \sum\limits_{n=1}^{p}\cos nx = \frac{\sin \left(p+\frac{1}{2}\right)x}{2\sin x/2}-\frac{1}{2}\right]
\end{equation*}
The remainder,
\begin{equation*}
R_{p}(x) = \sum\limits_{n=p+1}^{\infty}\frac{\sin nx}{n} =f(x)-s_{p}(x) = \frac{\pi-x}{2}-s_{p}(x)
\end{equation*}
\begin{equation}
\therefore \quad R_{p}(x)=\frac{\pi}{2}- \frac{1}{2}\int\limits_{0}^{x}\frac{\sin\left[\left(p+\frac{1}{2}\right)u\right]}{\sin u/2}\,du \tag{5.5.9}
\end{equation}
or,
\begin{equation}
R_{p}(x)=\frac{\pi}{2}- \int\limits_{0}^{(p+1/2)x}\frac{\sin u}{u}\,du +\rho_{p}(x)\tag{5.5.10}
\end{equation}
where
\begin{equation}
\rho_{p}(x)=\int\limits_{0}^{x}\left\{ \frac{\sin u/2 -u/2}{u \sin u/2}\right\}\sin \left[\left(p+\frac{1}{2}\right)u\right]\,du\tag{5.5.11}
\end{equation}
On differentiating equation (5.5.10) with respect to ’x’, we find that \(R_{p}(x)\) has maxima or minima at
\begin{equation*}
x_{k}=\frac{2\pi k}{2p+1} \quad (k=0,1,2,\cdots)
\end{equation*}
The value of \(R_{p}(x)\) at \(x_{k}\) is
\begin{equation}
R_{p}(x)=\frac{\pi}{2}-\int\limits_{0}^{\pi k}\frac{\sin u}{u}\,du + \rho_{p}\left(\frac{2\pi k}{2p+1}\right)\tag{5.5.12}
\end{equation}
As \(p\rightarrow \infty\) for fixed \(k, \rho_{p}\rightarrow 0.\)
Hence the remainder, the deviation of the approximation from \((\pi-x)/2\) at \(x_{k}\) which approaches the point of the discontinuity at \(x=0\)(end point), tends to the limit
\begin{equation}
\displaystyle{\lim_{p \to \infty}} R_{p}(x_{k}) \rightarrow \frac{\pi}{2}-\int\limits_{0}^{\pi_{k}}\frac{\sin u}{u}\, du\tag{5.5.13}
\end{equation}
For \(k=1\text{,}\) we find that
\begin{equation*}
\displaystyle{\lim_{p \to \infty}} R_{p}(x_{1}) \rightarrow \frac{\pi}{2}-\int\limits_{0}^{\pi}\frac{\sin u}{u}\, du
\end{equation*}
\begin{equation}
= \frac{\pi}{2}-\frac{\pi}{2}(1.179) = -0.281\tag{5.5.14}
\end{equation}
Hence the negative sign in equation (5.5.14) indicates that the approximate curve for \(f(x)\) is overshooted by about m\(18 \% \) at a jump discontinuity (i.e., at \(x=0\)), in the Fourier series.
