Subsection 1.1.6 Scalar Triple Product
- Definition: Let \(\vec{a}\text{,}\) \(\vec{b}\text{,}\) and \(\vec{c}\) be three vectors then their scalar triple product is determined by \(\vec{a}\cdot{(\vec{b}\times\vec{c})}\) and \([\vec{a}\vec{b}\vec{c}]\text{.}\) If \(\vec{a} = a_{1}\hat{i}+a_{2}\hat{j}+ a_{3}\hat{k}\) \(\vec{b} = b_{1}\hat{i}+b_{2}\hat{j}+ b_{3}\hat{k}, \) and \(\vec{c} = c_{1}\hat{i}+c_{2}\hat{j}+ c_{3}\hat{k}\) then\begin{align*} \vec{a}\cdot{(\vec{b}\times\vec{c})} \amp = (a_{1}\hat{i}+a_{2}\hat{j} + a_{3}\hat{k}) \cdot{\begin{Vmatrix} \hat{i} & \hat{j} & \hat{k} \\ b_{1} & b_{2} & b_{3}\\c_{1} & c_{2} & c_{3} \end{Vmatrix}} \end{align*}\begin{equation*} =(a_{1}\hat{i}+a_{2}\hat{j}+ a_{3}\hat{k}) \end{equation*}\begin{equation*} \cdot [(b_{2}c_{3}-b_{3}c_{2})\hat{i} - (b_{1}c_{3}-b_{3}c_{1})\hat{j} + (b_{1}c_{2}-b_{2}c_{1})\hat{k}] \end{equation*}\begin{equation*} =a_{1}(b_{2}c_{3}-b_{3}c_{2}) + a_{2}(b_{3}c_{1}-b_{1}c_{3}) + a_{3}(b_{1}c_{2}-b_{2}c_{1}) \end{equation*}\begin{equation*} =\begin{Vmatrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3}\\ c_{1} & c_{2} & c_{3} \end{Vmatrix} = [\vec{a}\vec{b}\vec{c}] \end{equation*}From the properties of a determinant, we can find that the value of the product depends upon the cyclic order of the vectors and is independent of the position of the dot and cross. Thus, dot and cross may be interchangeable in a scalar triple product, i.e.,\begin{align*} [\vec{a}\vec{b}\vec{c}] \amp = [\vec{c}\vec{a}\vec{b}] = [\vec{b}\vec{c}\vec{a}]\\ \text{or,}\quad \vec{a}\cdot{(\vec{b}\times\vec{c})} \amp = \vec{c}\cdot{(\vec{a}\times\vec{b})} = \vec{b}\cdot{(\vec{c}\times\vec{a})} \end{align*}The value of product changes in sign if the order is non-cyclic, i.e., \([\vec{a}\vec{b}\vec{c}] = -[\vec{b}\vec{a}\vec{c}] = -[\vec{a}\vec{c}\vec{b}]\)
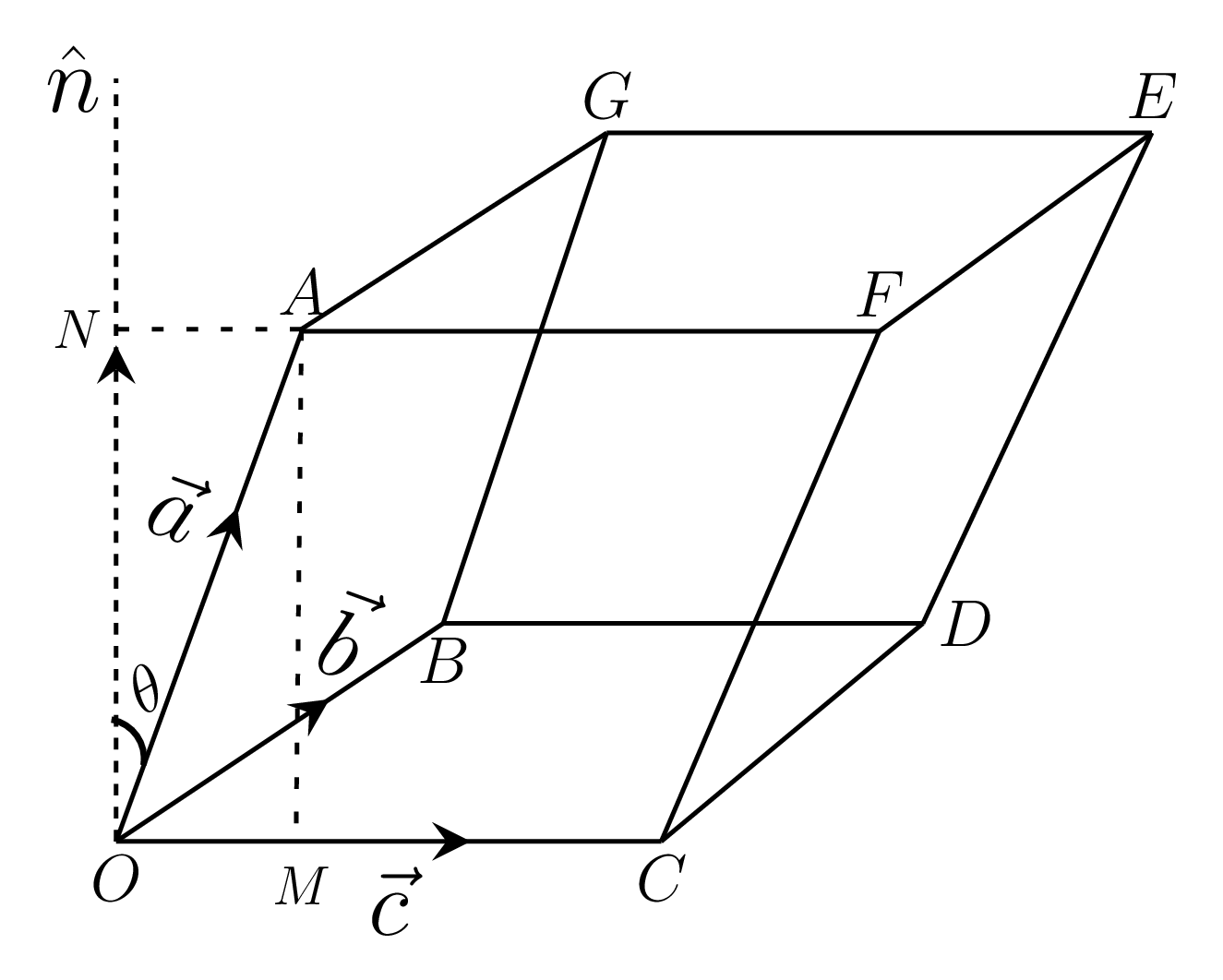
- Geometrical Interpretation: Let \(\vec{a}\text{,}\) \(\vec{b}\text{,}\) and \(\vec{c}\) be the co-terminous edges of the parallelopiped, as shown in figure Figure 1.1.10, then\begin{align*} \vec{a}\cdot{(\vec{b}\times\vec{c})} \amp = \vec{a}\cdot (\text{area of} \parallel^{gm} \,OBDC)\hat{n} \\ \amp= (\text{area of} \parallel^{gm}OBDC) (\text{projection of} \vec{a} \quad \text{on} \hat{n}) \\ \amp = (\text{area of} \parallel^{gm}OBDC) (a \cos\theta) \\ \amp = (\text{area of} \parallel^{gm}OBDC) \text{(height of the parallelopiped)} \\ \amp = \text{Volume of the parallelopiped}. \end{align*}That is, the scalar triple product gives the volume of the parallelopiped having these vectors as co-terminous edges.
Note: If \(\vec{a}\cdot{(\vec{b}\times\vec{c})} = 0\text{,}\) then \(\vec{a}\text{,}\) \(\vec{b}\text{,}\) \(\vec{c}\) are coplanars, and
\begin{equation*}
\text{ Volume of tetrahedron} = \frac{1}{6}[\vec{a}\vec{b}\vec{c}].
\end{equation*}
