Subsection 3.4.1 The Stress Tensor
The stress tensor is defined as the internal force per unit area acting on a deformed body. The stress may be directed normally or tangentially to the surfaces on which force act. If the deforming force act normally to a given area of an elastic medium, they produce pure elongations and in that case the stresses are called “ tensile or normal stresses” and if deforming forces act tangentially ’shearing stresses’ are produced.
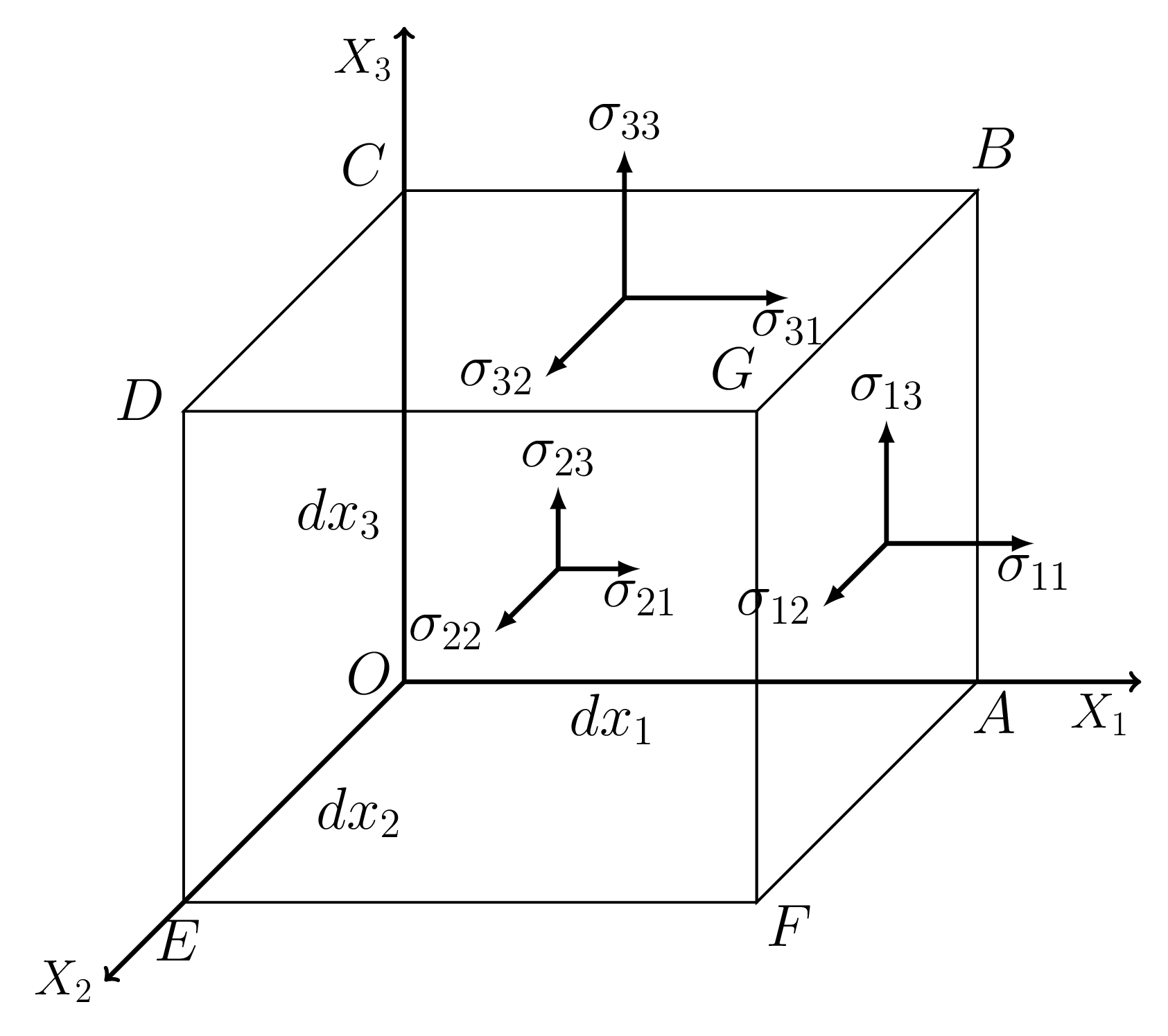
Consider a rectangular parallelopiped \(ABCDEFG\) of volume \(\,dx_{1}dx_{2}dx_{3}\text{,}\) as shown in Figure 3.4.2. Let a deforming force \(\vec{F}\) acts on it so that
\begin{equation}
\vec{F}= \left\{F_{1},F_{2},F_{3}\right\}\tag{3.4.5}
\end{equation}
Let a component \(F_{1}\) acts normal to the face $ABGF$ of area \(A_{1} = \,dx_{2}dx_{3}\text{,}\) then the stress acting normal to this face, \(\sigma_{11}\) is defined as
\begin{equation}
\sigma_{11} = \frac{\partial F_{1}}{\partial A_{1}} \tag{3.4.6}
\end{equation}
similarly, stress normal to the face OABC is defined as
\begin{equation}
\sigma_{22} = \frac{\partial F_{2}}{\partial A_{2}}\tag{3.4.7}
\end{equation}
and the stress normal to the face OEFA is
\begin{equation}
\sigma_{33} = \frac{\partial F_{3}}{\partial A_{3}}\tag{3.4.8}
\end{equation}
where \(A_{2}=\,dx_{3}\,dx_{1}\text{,}\) and \(A_{3}=\,dx_{1}\,dx_{2}\text{.}\) Thus \(\sigma_{11} {,} \sigma_{22}\text{,}\) and \(\sigma_{33}\) are normal stresses acting on a volume element. Now, consider the tangential forces acting on the face \(ABGF\text{,}\) i.e., forces acting along \(X_{2}\) and \(X_{3}\) directions, then the shearing stress in \(X_{2}\) - direction acting on a plane perpendicular to the \(X_{1}\)- direction, may be defined by
\begin{equation}
\sigma_{12} = \frac{\partial F_{2}}{\partial A_{1}}\tag{3.4.9}
\end{equation}
when the force is along \(X_{3}\)- direction acting on the same face \(ABGF\text{,}\) the shearing stress is defined by
\begin{equation}
\sigma_{13} = \frac{\partial F_{3}}{\partial A_{1}}\tag{3.4.10}
\end{equation}
similarly, the tangential or shearing stresses acting on the face OABC perpendicular to the \(X_{2}\)- direction along \(X_{1}\) and \(X_{3}\) directions are given by
\begin{equation}
\sigma_{21} = \frac{\partial F_{1}}{\partial A_{2}}\tag{3.4.11}
\end{equation}
and
\begin{equation}
\sigma_{23} = \frac{\partial F_{3}}{\partial A_{2}}\tag{3.4.12}
\end{equation}
and those acting on the face OEFA perpendicular to the \(X_{3}\)- direction along \(X_{2}\) and \(X_{1}\) directions are given by
\begin{equation}
\sigma_{32} = \frac{\partial F_{2}}{\partial A_{3}}\tag{3.4.13}
\end{equation}
\begin{equation}
\sigma_{31} = \frac{\partial F_{1}}{\partial A_{3}}\tag{3.4.14}
\end{equation}
Hence total stress may be completely specified by matrix form as
\begin{equation}
T = \begin{bmatrix}
\sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} \\
\sigma_{31} & \sigma_{32} & \sigma_{33}
\end{bmatrix}\tag{3.4.15}
\end{equation}
Since the shearing stresses on mutually perpendicular planes are always equal, we have -
\begin{equation*}
\sigma_{12}= \sigma_{21} {;} \quad \sigma_{13}= \sigma_{31} {;} \quad \sigma_{23}= \sigma_{32}
\end{equation*}
because when volume element to be in static equilibrium, the moment of force along \(X_{3}\) - direction would be
\begin{equation*}
(\sigma_{12}\,dx_{2}\,dx_{3})\,dx_{1} = (\sigma_{21}\,dx_{1}dx_{3})\,dx_{2}
\end{equation*}
Therefore \(\sigma_{12} = \sigma_{21}\) which is given by the faces ABGF and DEFG. Thus stress matrix has only six independent components for its complete specification.
\begin{equation*}
T = \begin{bmatrix}
\frac{\partial F_{1}}{\partial A_{1}} & \frac{\partial F_{2}}{\partial A_{1}} &
\frac{\partial F_{3}}{\partial A_{1}} \\ \frac{\partial F_{1}}{\partial A_{2}} &
\frac{\partial F_{2}}{\partial A_{2}} & \frac{\partial F_{3}}{\partial A_{2}} \\
\frac{\partial F_{1}}{\partial A_{3}} & \frac{\partial F_{2}}{\partial A_{3}} &
\frac{\partial F_{3}}{\partial A_{3}}
\end{bmatrix}
\end{equation*}
or,
\begin{equation}
T = \begin{bmatrix}
\frac{\partial}{\partial A_{1}}\\\frac{\partial}{\partial A_{2}}\\\frac{\partial}{\partial A_{3}}
\end{bmatrix} \begin{bmatrix}
F_{1} & F_{2} & F_{3}
\end{bmatrix} \tag{3.4.16}
\end{equation}
Now, since the force \(F_{i} = \begin{bmatrix}
F_{1} & F_{2} & F_{3}
\end{bmatrix}\) is definitely a vector and if \(\begin{bmatrix}
\frac{\partial}{\partial A_{1}}\\ \frac{\partial}{\partial A_{2}}\\ \frac{\partial}{\partial A_{3}}
\end{bmatrix}\) is a vector, then \(T\) will certainly be a tensor of rank two. Since, Area is a vector, it must transform like vector, therefore,
\begin{equation}
\bar{A_{j}} = \frac{\partial x^{i}}{\partial \bar{x}^{j}}A_{i} = a_{ij}A_{i}\tag{3.4.17}
\end{equation}
Now,
\begin{equation}
\frac{\partial}{\partial \bar{A}_{j}} = a_{ij}\frac{\partial}{\partial A_{i}}\tag{3.4.18}
\end{equation}
which is a vector transformation law. Thus, stress matrix eqn. (3.4.15) is a tensor of rank two and is called a ’stress tensor’.
