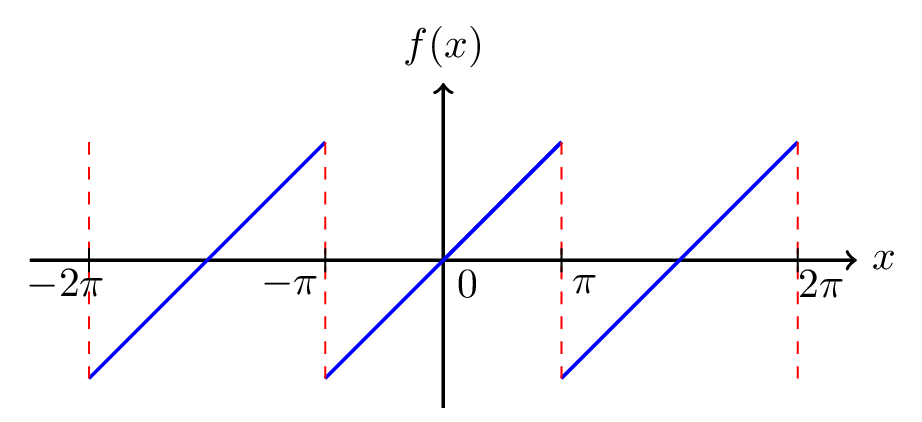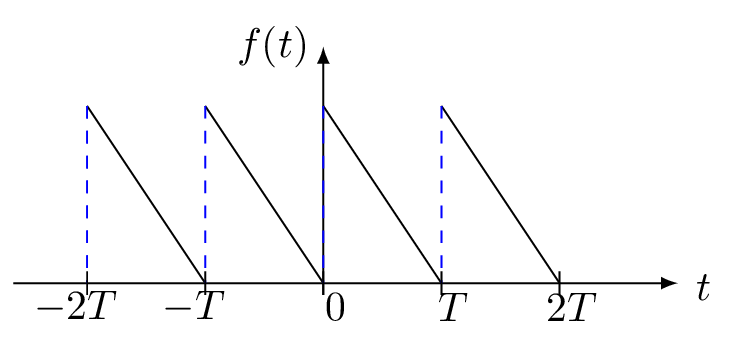Skip to main content

Mathematical Methods of Physics: For Undergraduate

Sunil Karna

Section 5.6 Examples C

Example 5.6.1.

A periodic function of period 4 is defined as \(f(x) = |x|\) for \(-2 \leq x \leq 2\text{.}\) Find its Fourier series expansion.
Solution.
Here, \(f(-x) =|-x| = |x| = f(x)\) and so is even. Therefore it can be expanded only in cosine series and the coefficients can be evaluated from half range only. i.e., the Fourier series is
\begin{equation} f(x) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos \left(\frac{n\pi x}{c}\right)\right] \tag{5.6.1} \end{equation}
where
\begin{equation*} a_{0}= \frac{2}{c}\int\limits_{0}^{c}f(x) \,dx = \frac{2}{2}\int\limits_{0}^{2}|x| \,dx =\int\limits_{0}^{2}x \,dx = 2. \end{equation*}
\begin{equation*} a_{n}= \frac{2}{c}\int\limits_{0}^{c}f(x)\cos \left(\frac{n\pi x}{c}\right) \,dx \end{equation*}
\begin{equation*} = \frac{2}{c}\int\limits_{0}^{c}|x|\cos \left(\frac{n\pi x}{c}\right) \,dx = \frac{2}{2}\int\limits_{0}^{2}x\cos \left(\frac{n\pi x}{2}\right) \,dx \end{equation*}
\begin{equation*} =\left[x \frac{2}{n\pi}\sin \left(\frac{n\pi x}{2}\right) -1-\frac{4}{-n^{2}\pi^{2}}\cos \left(\frac{n\pi x}{2}\right)\right]_{0}^{2} \end{equation*}
\begin{equation*} =0+\frac{4}{n^{2}\pi^{2}}(\cos n\pi-1) \end{equation*}
\begin{equation*} =\frac{4}{n^{2}\pi^{2}}\left[(-1)^{n}-1\right] = \begin{cases} -\frac{8}{n^{2}\pi^{2}},\quad \text{if n is odd}\\ 0, \quad \text{if n is even} \end{cases} \end{equation*}
\begin{equation} f(x) = 1-\frac{8}{\pi^{2}}\left[\frac{\cos \pi x/2}{1^{2}}+\frac{\cos 3\pi x/2}{3^{2}}+\frac{\cos 5\pi x/2}{5^{2}}+\cdots\right] \tag{5.6.2} \end{equation}

Example 5.6.2.

Find the Fourier series expansion of the periodic function of period \(1\text{.}\)
\begin{equation*} f(x)= \begin{cases} \frac{1}{2}+x, \quad \text{for} \quad -1/2 \lt x \lt 0\\ \frac{1}{2}-x,\quad \text{for}\quad 0 \lt x \lt 1/2. \end{cases} \end{equation*}
Solution.
Here, \(2c=1,\) \(\therefore c = 1/2\text{.}\)
\begin{equation*} a_{0}= \frac{1}{c}\int\limits_{-c}^{c}f(x) \,dx \end{equation*}
\begin{equation*} = \frac{1}{1/2}\left[\int\limits_{-1/2}^{0}\left( \frac{1}{2}+x\right) \,dx + \int\limits_{0}^{1/2}\left( \frac{1}{2}+x\right) \,dx\right] \end{equation*}
\begin{equation*} =2\left[\left\{\frac{x}{2}+\frac{x^{2}}{2}\right\}_{-1/2}^{0} + \left\{\frac{x}{2}-\frac{x^{2}}{2}\right\}_{0}^{1/2}\right] \end{equation*}
\begin{equation*} =2\left[\frac{1}{2}\left\{+\frac{1}{2}-\frac{1}{4}\right\} +\frac{1}{2}\left\{\frac{1}{2}-\frac{1}{4}\right\}\right] = \frac{1}{2}. \end{equation*}
\begin{equation*} a_{n}= \frac{1}{c}\int\limits_{-c}^{c}f(x)\cos \left(\frac{n\pi x}{c}\right) \,dx \end{equation*}
\begin{equation*} = 2\left[\int\limits_{-1/2}^{0}\left( \frac{1}{2}+x\right)\cos \left(\frac{n\pi x}{1/2}\right) \,dx \right. \end{equation*}
\begin{equation*} \left.+ \int\limits_{0}^{1/2}\left( \frac{1}{2}-x\right)\cos \left(\frac{n\pi x}{1/2}\right) \,dx\right] \end{equation*}
\begin{equation*} = 2\left[\int\limits_{-1/2}^{0}\left( \frac{1}{2}+x\right)\cos 2n\pi x\,dx +\int\limits_{0}^{1/2}\left( \frac{1}{2}-x\right)\cos 2n\pi x\,dx\right] \end{equation*}
\begin{equation*} =\frac{1}{\pi^{2}}\left[\frac{1}{n^{2}}-\frac{(-1)^{n}}{n}\right] =\begin{cases} \frac{2}{n^{2}\pi^{2}}, & \text{if n is odd}\\ 0, & \text{if n is even}. \end{cases} \end{equation*}
\begin{equation*} b_{n}= \frac{1}{c}\int\limits_{-c}^{c}f(x)\sin \left(\frac{n\pi x}{c}\right) \,dx =0 \end{equation*}
\begin{equation*} \therefore f(x) = \frac{1}{4}+\frac{2}{\pi^{2}}\left[\frac{\cos \pi x}{1^{2}}+\frac{\cos 3\pi x}{3^{2}}+\frac{\cos 5\pi x}{5^{2}}+\cdots\right] \end{equation*}

Example 5.6.3.

Expand \(f(x) = e^{x}\) in cosine series over [0,1].
Solution.
\begin{equation*} f(x) = e^{x}= \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos \left(\frac{n\pi x}{c}\right)\right] \end{equation*}
where,
\begin{equation*} a_{0}= \frac{2}{c}\int\limits_{0}^{c}f(x) \,dx = \frac{2}{1}\int\limits_{0}^{1} e^{x}\,dx = 2\left(e^{x}\right)_{0}^{1}=2(e^{1}-1). \end{equation*}
\begin{equation*} a_{n}= \frac{2}{c}\int\limits_{0}^{c}f(x)\cos \left(\frac{n\pi x}{c}\right) \,dx = \frac{2}{1}\int\limits_{0}^{1}e^{x}\cos n\pi x \,dx \end{equation*}
\begin{equation*} =2\left[\frac{e^{x}}{1+n^{2}\pi^{2}}(\cos n\pi x + n \pi \sin n\pi x)\right]_{0}^{1} \end{equation*}
\begin{equation*} =2\left[\frac{e^{1}}{1+n^{2}\pi^{2}}(\cos n\pi + n \pi \sin n\pi -1-0)\right]_{0}^{1} = \frac{2e^{1}}{1+n^{2}\pi^{2}}\left[(-1)^{n}-1)\right] \end{equation*}
\begin{equation*} \therefore \quad e^{x} = (e^{1}-1)+\sum\limits_{n=1}^{\infty}\frac{2e^{1}}{1+n^{2}\pi^{2}}\left[(-1)^{n}-1)\right]\cos n \pi x. \end{equation*}

Example 5.6.4.

Find a series of sines of multiples of which will represent in the interval.
Solution.
Let
\begin{equation*} f(x) = \sum\limits_{n=1}^{\infty}\left[b_{n}\sin nx\right] \end{equation*}
where,
\begin{equation*} b_{n}= \frac{2}{\pi}\int\limits_{0}^{\pi}f(x)\sin nx \,dx = \frac{2}{\pi}\int\limits_{0}^{\pi}x\sin nx \,dx \end{equation*}
\begin{equation*} = \frac{2}{\pi}\left[x.\frac{\cos nx}{-n}-1.\frac{\sin nx}{-n^{2}}\right]^{\pi}_{0} \end{equation*}
\begin{equation*} = \frac{2}{\pi}\left[\pi.\frac{\cos n\pi}{-n}-1.\frac{\sin n\pi}{-n^{2}}\right] = -\frac{2}{n}(-1)^{n}=(-1)^{n+1}\frac{2}{n} \end{equation*}
\begin{equation*} \therefore \quad x = \sum\limits_{n=1}^{\infty}\left[2(-1)^{n+1}\right]\frac{\sin nx}{n} \end{equation*}

Example 5.6.5.

A saw tooth wave is given by \(f(x) = x\) for \(-\pi \leq x \leq \pi\) or, \(f(t) = a(1-t/T)\) for \(0 \leq t \leq T\text{,}\) find the Fourier series representation of the wave.
Solution.
The Fourier series expansion of a function \(f(x)\) is written as:
\begin{equation*} f(x) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos nx + b_{n}\sin nx\right], \end{equation*}
where,
\begin{equation*} a_{0}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \,dx = \frac{1}{\pi}\int\limits_{-\pi}^{\pi} x\,dx = 0. \end{equation*}
\begin{equation*} a_{n}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \cos nx\,dx = \frac{1}{\pi}\int\limits_{-\pi}^{\pi}x \cos nx \,dx = 0 \end{equation*}
and
\begin{equation*} b_{n}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \sin nx\,dx = \frac{1}{\pi}\int\limits_{-\pi}^{\pi}x\sin nx\,dx = -\frac{2}{n}\cos n\pi = (-1)^{n+1}\frac{2}{n} \end{equation*}
\begin{equation*} \therefore f(x) = x = 2\sum\limits_{n=1}^{\infty}\left[(-1)^{n+1}\frac{\sin nx}{n}\right] \end{equation*}
The graphical representation of the functions \(f(x)\) and \(f(t)\) is shown in figure below.
or,
\begin{equation*} f(t) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos \left(\frac{n\pi t}{T}\right) + b_{n}\sin \left(\frac{n\pi t}{T}\right)\right] \end{equation*}
where,
\begin{equation*} a_{0}= \frac{2}{T}\int\limits_{0}^{T}f(t) \,dt = \frac{2}{T}\int\limits_{0}^{T}a\left(1-\frac{t}{T}\right)\,dt \end{equation*}
\begin{equation*} =\frac{2a}{T}\left[t-\frac{t^{2}}{2T}\right]_{0}^{T}= \frac{2a}{T}\left[T-\frac{T^{2}}{2T}\right] = a \end{equation*}
which gives the ordinate of the axis of the curve.
\begin{equation*} a_{n}= \frac{2}{T}\int\limits_{0}^{T}f(t) \cos \left(\frac{n\pi t}{T}\right)\,dt = \frac{2}{T}\int\limits_{0}^{T}a\left(1-\frac{t}{T}\right) \cos \left(\frac{n\pi t}{T}\right)\,dt \end{equation*}
\begin{equation*} = \frac{2a}{T}\int\limits_{0}^{T}\cos \left(\frac{n\pi t}{T}\right)\,dt - \frac{2a}{T^{2}}\int\limits_{0}^{T}t\cos \left(\frac{n\pi t}{T}\right)\,dt \end{equation*}
\begin{equation*} =- \frac{2a}{T^{2}}\int\limits_{0}^{T}t\cos \left(\frac{n\pi t}{T}\right)\,dt \end{equation*}
\begin{equation*} = -\frac{2a}{T^{2}}\left[t.\frac{(\sin n\pi t/T)}{n\pi/T}-1.\frac{\cos (n\pi t/T)}{-n^{2}\pi^{2}/T^{2}}\right]_{0}^{T} \end{equation*}
\begin{equation*} \left[ \because \quad \int\limits_{0}^{T}\cos \left(\frac{n \pi t}{T}\right)\,dt =0\right] \end{equation*}
\begin{equation*} =-\frac{2a}{T^{2}}\left[T.\frac{\sin n\pi}{n\pi/T}+\frac{\cos n\pi}{n^{2}\pi^{2}/T^{2}}-0-\frac{1}{n^{2}\pi^{2}/T^{2}}\right] \end{equation*}
\begin{equation*} =\frac{2a}{T^{2}(n^{2}\pi^{2}/T^{2})}\left[1-(-1)^{n}\right] =\begin{cases} 0, & \text{for n is even}\\ \frac{4a}{n^{2}\pi^{2}}, & \text{for n is odd}. \end{cases} \end{equation*}
However, if the wave is expressed in terms of angular velocity \(\omega\text{,}\) the term \(\cos (n\pi t/T)\) had better replaced by \(cos n\omega t\) and in that case \(a_{n}=0\text{.}\) \([\because \omega = \frac{2\pi}{T}]\text{.}\) For \(b_{n}\text{,}\) we have
\begin{equation*} b_{n} = \frac{2}{T}\int\limits_{0}^{T}f(t) \sin \left(\frac{n\pi t}{T}\right)\,dt = \frac{2}{T}\int\limits_{0}^{T}a\left(1-\frac{t}{T}\right) \sin \left(\frac{n\pi t}{T}\right)\,dt \end{equation*}
\begin{equation*} =\frac{2a}{T}\int\limits_{0}^{T} \sin \left(\frac{n\pi t}{T}\right)\,dt-\frac{2a}{T^{2}}\int\limits_{0}^{T} t\sin \left(\frac{n\pi t}{T}\right)\,dt \end{equation*}
\begin{equation*} =\frac{2a}{T}\left[\frac{\cos (n\pi t/T)}{-n\pi/T}\right]_{0}^{T}-\frac{2a}{T^{2}}\left[t\frac{\cos (n\pi t/T)}{-n\pi/T}-1.\frac{\sin (n\pi t/T)}{-n^{2}\pi^{2}/T^{2}}\right]_{0}^{T} \end{equation*}
\begin{equation*} = \frac{2a}{T}\left[\frac{T\cos n\pi}{-n\pi}+\frac{T}{n\pi}\right]-\frac{2a}{T^{2}}\left[\frac{T \cos n\pi}{-n\pi/T}-0+\frac{\sin n\pi}{n^{2}\pi^{2}/T^{2}}-0\right] = \frac{2a}{n\pi} \end{equation*}
\begin{equation*} \therefore \quad f(t) = \frac{a}{2}+\sum\limits_{n=1}^{\infty}\left[\frac{2a}{n^{2}\pi^{2}}\left\{1-(-1)^{n}\right\} \cos \left(\frac{n\pi t}{T}\right)+\frac{2a}{n\pi} \sin \left(\frac{n\pi t}{T}\right)\right]. \end{equation*}
The graph of the given function is shown in figure below.

Example 5.6.6.

Triangular wave is given by
\begin{equation*} f(x) = \begin{cases} 2at/T, \quad \text{for} \quad 0 \lt t \lt T/2\\ 2a(T-t)/T, \quad \text{for} \quad T/2 \lt t \lt T. \end{cases} \end{equation*}
Solution.
\begin{equation*} f(t) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos n\omega t + b_{n}\sin n\omega t\right], \end{equation*}
where
\begin{equation*} a_{0}= \frac{2}{T}\int\limits_{0}^{T}f(t) \,dt = \frac{2}{T}\left[\int\limits_{0}^{T/2} \frac{2\omega t}{T}\,dt + \int\limits_{T/2}^{T} \frac{2\omega (T-t)}{T}\,dt\right] \end{equation*}
\begin{equation*} =\frac{2}{T}\left[\frac{2a}{T}\left(\frac{t^{2}}{2}\right)_{0}^{T/2}+\frac{2a}{T}\left(Tt-\frac{t^{2}}{2}\right)_{T/2}^{T}\right] \end{equation*}
\begin{equation*} =\frac{4a}{T^{2}}\left[\frac{T^{2}}{8}+\left(T^{2}-\frac{T^{2}}{2}\right)-\left(\frac{T^{2}}{2}-\frac{T^{2}}{8}\right)\right] = a. \end{equation*}
This is the displacement of the axis of the curve from the axis of the co-ordinate system. Now,
\begin{equation*} a_{n}= \frac{2}{T}\int\limits_{0}^{T}f(t) \cos n\omega t \,dt=\frac{4a}{T^{2}}\left[\frac{2}{n^{2}\omega^{2}}\left\{(-1)^{n}-1\right\}\right] \end{equation*}
\begin{equation*} =\frac{4a}{T^{2}}\left[\frac{2}{n^{2}(2\pi/T)^{2}}\left\{(-1)^{n}-1\right\}\right] \end{equation*}
\begin{equation*} =\frac{2a}{n^{2}\pi^{2}}\left\{(-1)^{n}-1\right\} =\begin{cases} 0, & \text{if n is even}\\ -\frac{4a}{n^{2}\pi^{2}}. & \text{if n is odd} \end{cases} \end{equation*}
thus only odd harmonics with cosine terms would appear in the series.
\begin{equation*} b_{n}= \frac{2}{T}\int\limits_{0}^{T}f(t) \sin n\omega t \,dt \end{equation*}
\begin{equation*} =\frac{2}{T}\left[\int\limits_{0}^{T/2}\frac{2at}{T} \sin n\omega t \, dt + \int\limits_{T/2}^{T}\frac{2a(T-t)}{T} \sin n\omega t \,dt\right] \end{equation*}
\begin{equation*} =\frac{4a}{T^{2}}\left[\int\limits_{0}^{T/2} t \sin n\omega t \,dt + \int\limits_{T/2}^{T} T \sin n\omega t \,dt - \int\limits_{T/2}^{T} \sin n\omega t \,dt\right] = 0. \end{equation*}
Hence,
\begin{equation*} f(t) = \frac{a}{2}-\frac{4a}{\pi^{2}}\sum\limits_{n=1}^{\infty}\frac{\cos n\omega t}{n^{2}}, \end{equation*}
where n is an odd number.

Example 5.6.7.

Find the Fourier series expansion a given square - wave
\begin{equation*} f(x) = \begin{cases} 0, & \text{for} \quad -\pi \leq x \leq 0 \\ h, & \text{for} \quad 0 \leq x \leq \pi \end{cases} \end{equation*}
or,
\begin{equation*} f(t) = \begin{cases} -1, & \text{for} \quad 0 \leq x \lt T/2 \\ 0, & \text{for} \quad t =T/2\\ +1, & \text{for} \quad T/2 \lt t \lt T \end{cases} \end{equation*}
Solution.
Let
\begin{equation*} f(x) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos nx + b_{n}\sin nx\right] \end{equation*}
where
\begin{equation*} a_{0}=\frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \,dx = \frac{1}{\pi}\left[\int\limits_{-\pi}^{0}f(x) \,dx + \int\limits_{0}^{\pi}f(x) \,dx\right] \end{equation*}
\begin{equation*} = \frac{1}{\pi}\left[\int\limits_{-\pi}^{0}0.\,dx + \int\limits_{0}^{\pi}h\,dx\right] = \frac{1}{\pi}\left[h(x)_{0}^{\pi}\right] = \frac{h}{\pi}(\pi) = h. \end{equation*}
\begin{equation*} a_{n}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \cos nx \,dx=\frac{1}{\pi}\left[\int\limits_{-\pi}^{0}0.\cos nx\,dx + \int\limits_{0}^{\pi}h.\cos nx\,dx\right] \end{equation*}
\begin{equation*} =\frac{h}{\pi}\left[\int\limits_{0}^{\pi}\cos nx\,dx\right] = \frac{h}{\pi}\left[\left(\frac{\sin nx}{n}\right)_{0}^{\pi}\right]=0 \end{equation*}
\begin{equation*} b_{n}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \sin nx \,dx=\frac{1}{\pi}\left[\int\limits_{-\pi}^{0}0.\sin nx\,dx + \int\limits_{0}^{\pi}h.\sin nx\,dx\right] \end{equation*}
\begin{equation*} =\frac{h}{\pi}\left[\int\limits_{0}^{\pi}\sin nx \,dx\right]=\frac{h}{\pi}\left[-\frac{\cos nx}{n}\right]_{0}^{\pi} = \begin{cases} 0, & \text{for n even}\\ \frac{2h}{n\pi}, & \text{for n odd} \end{cases} \end{equation*}
Therefore, the required Fourier series is
\begin{equation*} f(x) = \frac{h}{2}+\frac{2h}{\pi}\sum\limits_{n_{odd}=1}^{\infty}\left[\frac{\sin nx}{n}\right]. \end{equation*}
The graphical representation of the functions \(f(x)\) is shown in the figure below.

Example 5.6.8.

A full - wave rectifier is given by
\begin{equation*} f(x) = \begin{cases} \sin x, & 0 \lt x \lt \pi\\ -\sin x, & -\pi \lt x \lt 0. \end{cases} \end{equation*}
Find the Fourier series expansion.
Solution.
Let
\begin{equation*} f(x) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos nx + b_{n}\sin nx\right] \end{equation*}
where
\begin{equation*} a_{0}=\frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \,dx = \frac{1}{\pi}\left[\int\limits_{-\pi}^{0}f(x) \,dx + \int\limits_{0}^{\pi}f(x) \,dx\right] \end{equation*}
\begin{equation*} =\frac{1}{\pi}\left[-\int\limits_{-\pi}^{0}\sin x\,dx + \int\limits_{0}^{\pi}\sin x\,dx\right] \end{equation*}
\begin{equation*} = \frac{2}{\pi} \int\limits_{0}^{\pi}\sin x\,dx = \frac{4}{\pi}. \end{equation*}
\begin{equation*} a_{n}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \cos nx \,dx=\frac{1}{\pi}\left[\int\limits_{-\pi}^{0}f(x)\cos nx\,dx + \int\limits_{0}^{\pi} f(x)\cos nx\,dx\right] \end{equation*}
\begin{equation*} =\frac{1}{\pi}\left[\int\limits_{-\pi}^{0}-\sin x \cos nx\,dx + \int\limits_{0}^{\pi}\sin x \cos nx\,dx\right] \end{equation*}
\begin{equation*} = \frac{2}{\pi}\int\limits_{0}^{\pi}\sin x \cos nx\,dx =\begin{cases} -\frac{4}{\pi(n^{2}-1)}, & \text{for n even}\\ 0, & \text{for n odd} \end{cases} \end{equation*}
and
\begin{equation*} b_{n}= \frac{1}{\pi}\int\limits_{-\pi}^{\pi}f(x) \sin nx \,dx \end{equation*}
\begin{equation*} =\frac{1}{\pi}\left[\int\limits_{-\pi}^{0}-\sin x \sin nx\,dx + \int\limits_{0}^{\pi} \sin x \sin nx\,dx\right] \end{equation*}
\begin{equation*} = \frac{2}{\pi}\int\limits_{0}^{\pi} \sin x \sin nx \,dx =1. \end{equation*}
\(\because\) for n=1, \(b_{1}=\frac{1}{2}\)]
Hence the required Fourier series is
\begin{equation*} f(x) = \frac{2}{\pi}-\frac{4}{\pi}\sum\limits_{n_{even}=2}^{\infty}\frac{\cos nx}{(n^{2}-1)}+\sin x \end{equation*}
The graphical representation of the functions \(f(x)\) is shown in figure below.
PrevTopNext