Section 3.4 Moment of Inertia Tensor
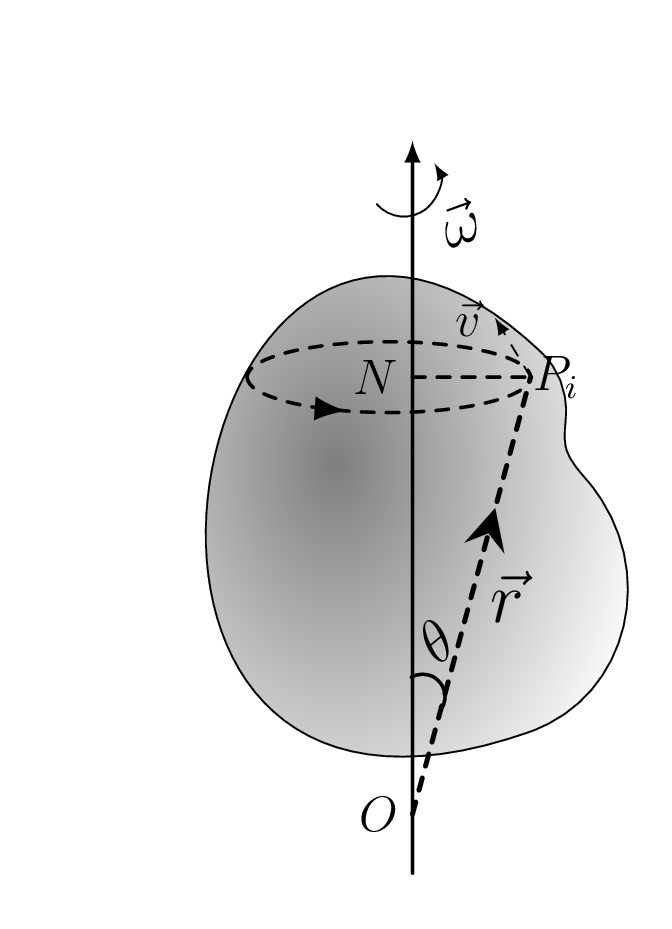
Consider a rigid body rotating about an axis that is passing through a point O as shown in figure Figure 3.4.1. Now the angular momentum of the body about such an axis is given by
\begin{equation*}
L = \sum\limits_{i}m_{i}(\vec{r_{i}}\times \vec{v_{i}}) = \sum\limits_{i}m_{i}(\vec{r_{i}}\times \vec{\dot{r}_{i}})
\end{equation*}
\begin{equation*}
= \sum\limits_{i}m_{i}[\vec{r_{i}}\times (\vec{\omega}\times\vec{r_{i}})] = \sum\limits_{i}m_{i}\left[\vec{\omega}r^{2}_{i} - (\vec{r_{i}}\cdot \vec{\omega})\vec{r_{i}}\right]
\end{equation*}
or,
\begin{equation*}
\hat{i}L_{x}+\hat{j}L_{y}+\hat{k}L_{z} = \sum\limits_{i}m_{i}\left[(\hat{i}\omega_{x}+ \hat{j}\omega_{y}+\hat{k}\omega_{z})r^{2}_{i} - (\vec{r_{i}}\cdot \vec{\omega})(\hat{i}x_{i}+\hat{j}y_{i}+\hat{k}z_{i})\right]
\end{equation*}
\begin{equation*}
= \sum\limits_{i}m_{i} \left[(\hat{i}\omega_{x} + \hat{j}\omega_{y}+\hat{k}\omega_{z})r^{2}_{i} - (x_{i}\omega_{x}+y_{i}\omega_{y}+z_{i}\omega_{z})(\hat{i}x_{i}+\hat{j}y_{i}+\hat{k}z_{i})\right]
\end{equation*}
\begin{equation*}
=\hat{i}\left[\omega_{x}\sum\limits_{i}m_{i}\left(r^{2}_{i}-x^{2}_{i}\right) - \omega_{y} \sum\limits_{i}m_{i}x_{i}y_{i} - \omega_{z}\sum\limits_{i}m_{i}x_{i}z_{i}\right]
\end{equation*}
\begin{equation*}
+ \hat{j}\left[-\omega_{x}\sum\limits_{i}m_{i}x_{i}y_{i} + \omega_{y}\sum\limits_{i}m_{i}\left(r^{2}_{i}-y^{2}_{i}\right) - \omega_{z}\sum\limits_{i}m_{i}y_{i}z_{i}\right]
\end{equation*}
\begin{equation*}
+ \hat{k}\left[-\omega_{x}\sum\limits_{i}m_{i}x_{i}z_{i} - \omega_{y}\sum\limits_{i}m_{i}y_{i}z_{i}+\omega_{z}\sum\limits_{i}m_{i}\left(r^{2}_{i}-z^{2}_{i}\right) \right]
\end{equation*}
\begin{equation*}
=\hat{i}\left[I_{xx}\omega_{x} +I_{xy}\omega_{y}+I_{xz}\omega_{z}\right] + \hat{j}\left[I_{yx}\omega_{x} +I_{yy}\omega_{y}+I_{yz}\omega_{z}\right]
\end{equation*}
\begin{equation*}
+\hat{k}\left[I_{zx}\omega_{x} +I_{zx}\omega_{y}+I_{zz}\omega_{z}\right]
\end{equation*}
or,
\begin{equation}
\begin{cases}
L_{x} = \left[I_{xx}\omega_{x} +I_{xy}\omega_{y}+I_{xz}\omega_{z}\right];\\
L_{y}=\left[I_{yx}\omega_{x} +I_{yy}\omega_{y}+I_{yz}\omega_{z}\right];\\
L_{z} = \left[I_{zx}\omega_{x} +I_{zx}\omega_{y}+I_{zz}\omega_{z}\right]
\end{cases}\tag{3.4.1}
\end{equation}
or,
\begin{equation*}
\begin{bmatrix}
L_{x} \\ L_{y} \\ L_{z}
\end{bmatrix} = \begin{bmatrix}
I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz}
\end{bmatrix} \begin{bmatrix}
\omega_{x} \\ \omega_{y} \\ \omega_{z}
\end{bmatrix}
\end{equation*}
\begin{equation}
\therefore \quad \vec{L_{i}}=I_{ij}\vec{\omega_{j}}\tag{3.4.2}
\end{equation}
Where,
\begin{equation}
\begin{cases}
I_{xx} = \sum\limits_{i}m_{i}\left(r^{2}_{i}-x^{2}_{i}\right); \\
I_{yy} = \sum\limits_{i}m_{i}\left(r^{2}_{i}-y^{2}_{i}\right); \\
\quad I_{zz} =\sum\limits_{i}m_{i}\left(r^{2}_{i}-z^{2}_{i}\right)
\end{cases}\tag{3.4.3}
\end{equation}
are the coefficients of a moment of inertia.
and
\begin{equation}
\begin{cases}
I_{xy} = I_{yx} = -\sum\limits_{i}m_{i}x_{i}y_{i}; \\
\quad I_{yz} = I_{zy} = -\sum\limits_{i}m_{i}y_{i}z_{i}; \\
\quad I_{zx} = I_{xz} = -\sum\limits_{i}m_{i}z_{i}x_{i}
\end{cases}\tag{3.4.4}
\end{equation}
are the product of inertia.
Eqn. (3.4.1) shows that the angular momentum \(\vec{L}\) is not necessarily parallel to the angular velocity \(\vec{\omega}\text{.}\) From eqn. (3.4.2) since \(\vec{L_{i}}\) and \(\vec{\omega_{j}}\) are tensors of rank one, then from quatient law it is clear that \(I_{ij}\) must be a tensor of rank two. The value of \(I_{ij}\) is given by eqns. (3.4.3) and (3.4.4), which is called a moment of inertia tensor of the body.
