Subsection 3.1.1 Contravarient and Covarient Tensors
Covariance and contravariance describe how the quantitative description of physical entities change with a change of basis. A covariant tensor is one that transforms in the same way as the coordinate system itself. This means that the components of the tensor change in a particular way when the coordinates of the system are changed. A contravariant tensor, on the other hand, transforms in the opposite way to the coordinate system. This means that the components of the tensor change in a particular way when the coordinates of the system are changed. For a contravariant vector to be basis independent, the components of the vector must contra-vary (opposite manner) with a change of basis to compensate. That is, the components must vary with the inverse transformation to that of the change of basis. These componets of vectors are said to be contravariant. Examples of vectors with contravariant componets include the position of an object (displacement) relative to an observer, or any derivative of position with respect to time including velocity, acceleration, and jerk. For a covariant vector to be basis-independent, the components of the vector must co-vary (same manner) with change of basis to remain representing the same vector. That is, the componets must vary by the same transformation as the change of basis. The componets of these vectors are said to be covariant. Examples of covariant vectors apear when taking a gradiant of a function.
If a set of components \(A^{j}\) of a physical quantity in a coordinate system \((x^{1}{,} x^{2}{,} x^{3}{,} \cdots{,} x^{n})\) are related to the set of components \(\bar{A}^{i}\) of the same quantity in another coordinate system \((\bar{x}^{1}{,} \bar{x}^{2}{,} \bar{x}^{3}{,} \cdots{,} \bar{x}^{n})\) by the transformation equation.
\begin{equation}
\bar{A}^{i} = \frac{\partial \bar{x}^{i} }{\partial x^{j}}A^{j}\quad [i, j = 1,2,3 \cdots n]\tag{3.1.1}
\end{equation}
then they are called components of a contravarient vector or contravarient tensor of rank one. Multiply eqn. (3.1.1) by \(\frac{\partial x^{k}}{\partial \bar{x}^{i}}\text{,}\) we get -
\begin{equation*}
\frac{\partial x^{k}}{\partial \bar{x}^{i}}\bar{A}^{i}
= \frac{\partial x^{k}}{\partial \bar{x}^{i}} \frac{\partial \bar{x}^{i} }{\partial x^{j}}A^{j}
= \frac{\partial x^{k}}{\partial x^{j}} A^{j} = \delta^{k}_{j}A^{j} = A^{k}
\end{equation*}
or, we can also say,
\begin{equation}
A^{j} = \frac{\partial x^{j}}{\partial \bar{x}^{i}}\bar{A}^{i}\tag{3.1.2}
\end{equation}
by replacing \(k\) with \(j\text{.}\)
\begin{equation*}
\delta_{j,k} =
\begin{cases}
1, & \text{if } j = k \\
0, & \text{if } j \neq k
\end{cases}
\end{equation*}
A set of quantities \(B\) is called the components of a covarient vector or covarient tensor of rank one if \(A^{k}B_{k}\) = invarient (a scalar) = \(\bar{A}^{k}\bar{B}_{k}\text{.}\) Or,
\begin{equation*}
\bar{A}^{k}\bar{B}_{k} = A^{k}B_{k} = \frac{\partial x^{k}}{\partial \bar{x}^{i}}\bar{A}^{i} B_{k}
= \frac{\partial x^{\alpha}}{\partial \bar{x}^{k}}\bar{A}^{k} B_{\alpha}
\end{equation*}
by changing \(k\) with \(\alpha\) and \(i\) with \(k\text{.}\) Or,
\begin{equation*}
\bar{A}^{k} \left[B_{k}-\frac{\partial x^{\alpha}}{\partial \bar{x}^{k}}B_{\alpha}\right] = 0
\end{equation*}
\begin{equation}
\therefore \bar{B}_{k} = \frac{\partial x^{\alpha}}{\partial \bar{x}^{k}}B_{\alpha}\tag{3.1.3}
\end{equation}
or,
\begin{equation}
\bar{A}_{j} = \frac{\partial x^{i}}{\partial \bar{x}^{j}}A_{i} \tag{3.1.4}
\end{equation}
also,
\begin{equation}
A_{i}=\frac{\partial \bar{x}^{j}}{\partial x^{i}}\bar{A}_{j}\tag{3.1.5}
\end{equation}
are covarient tensor of rank one.
If \(n^{2}\) quantities \(A^{kl}\) in a coordinate system \((x^{1}{,} x^{2}{,} x^{3}{,} \cdots{,} x^{n})\) are related to \(n^{2}\) other quantities \(\bar{A}^{ij}\) in another coordinates \((\bar{x}^{1}{,} \bar{x}^{2}{,} \bar{x}^{3}{,} \cdots{,} \bar{x}^{n})\) by the transformation eqn.
\begin{equation}
\bar{A}^{ij}=\frac{\partial \bar{x}^{i}}{\partial x^{k}} \frac{\partial \bar{x}^{j}}{\partial x^{l}} A^{kl}\tag{3.1.6}
\end{equation}
\(here, [i,j = 1,2,3, \cdots n]\text{,}\) The \(A^{kl}\) are the components of a second rank contravarient tensor. Similarly,
\begin{equation}
\bar{A}_{ij}=\frac{\partial x^{k}}{\partial \bar{x}^{i}} \frac{\partial x^{l}}{\partial \bar{x}^{j}} A_{kl}\tag{3.1.7}
\end{equation}
and the \(A_{kl}\) are the components of a second rank covarient tensor. Also,
\begin{equation}
\bar{A}^{i}_{j}=\frac{\partial \bar{x}^{i}}{\partial x^{k}} \frac{\partial x^{l}}{\partial \bar{x}^{j}} A^{k}_{l}\tag{3.1.8}
\end{equation}
and the \(A^{k}_{l}\) are the components of a second rank mixed tensor. Again,
\begin{equation}
\bar{A}^{prm}_{ij} = \frac{\partial \bar{x}^{p}}{\partial x^{q}} \frac{\partial \bar{x}^{r}}{\partial x^{s}} \frac{\partial \bar{x}^{m}}{\partial x^{t}} \frac{\partial x^{k}}{\partial \bar{x}^{i}} \frac{\partial x^{l}}{\partial \bar{x}^{j}}A^{qst}_{kl}\tag{3.1.9}
\end{equation}
and \(A^{qst}_{kl}\) are a components of fifth - rank mixed tensor.
Note: The contravarient tensor is represented by components in the directions of coordinate increase whereas a covarient tensor is represented by components in the directions orthogonal to constant coordinate surfaces. In case of a cartesian coordinate system, the coordinate direction \(x^{i}\) concides with the direction orthogonal to the constant \(x^{i}\) surface so that the direction between the covarient and contravarient tensors vanishes. Hence we can not distinguish between them in cartesian systems. The covariance or contravariance of the tensor components is not intrinsic property of the entity but this distinction is due to the way in which the entity is related to coordinate system to which it is referred. It is to be noted that in a cartesian system
\begin{equation*}
\frac{\partial x^{j}}{\partial \bar{x}^{i}}= \frac{\partial \bar{x}^{i}}{\partial x^{j}}.
\end{equation*}
That is, both these partial derivatives are equal to the direction cosines between \(\bar{x}^{i}\) - and \(x^{i}\) - axes. Hence there is no difference between contravariant and covariant transformations in cartesian coordinates. In other coordinate system this is not true in general, thus the difference in covariant and contravariant is observed.
The tensor whose components transform like coordinate differential are called contravariant tensors. In this expression
\begin{equation*}
\bar{A}^{i} = \sum\limits_{j=1}^{3}\frac{\partial \bar{x}^{i}}{\partial x^{j}}{A}^{j};
\end{equation*}
where \(\frac{\partial \bar{x}^{i}}{\partial x^{j}}\) are the coordinate differentials. For example:
- In cartesian coordinates \((x,y)\text{,}\) suppose the velocity components are \(\dot{x}=\frac{\,dx}{\,dt}\text{,}\) \(\dot{y}=\frac{dy}{dt}\text{;}\)
- In oblique coordinats \((\alpha{,}\beta)\) the velocity components are \(\dot{\alpha}=\frac{\,d \alpha}{\,dt}\text{,}\) \(\dot{\beta}=\frac{\,d \beta}{\,dt}\text{;}\) and
- In polar coordinates \((r, \theta)\text{,}\) the velocity components are \(\dot{r}=\frac{\,dr}{\,dt}\text{,}\) \(\dot{\theta}=\frac{\,d\theta}{\,dt}\text{.}\)
Since all these relations express the velocity of same particle, they are related to each other in the following way:
\begin{equation*}
\frac{\,d\alpha}{\,dt} = \frac{\,d\alpha}{\,dx} \frac{\,dx}{\,dt} + \frac{\,d\alpha}{\,dy}\frac{\,dy}{\,dt}
\end{equation*}
or,
\begin{equation*}
\dot{\alpha} = \frac{\,d\alpha}{\,dx} \dot{x} + \frac{\,d\alpha}{\,dy} \dot{y}
\end{equation*}
also,
\begin{equation*}
\dot{\beta} = \frac{\,d\beta}{\,dx}\dot{x} + \frac{\,d\beta}{\,dy} \dot{y}
\end{equation*}
Now,
\begin{equation*}
\dot{r} = \frac{\,dr}{\,dx} \dot{x} + \frac{\,dr}{\,dy}\dot{y}
\end{equation*}
and,
\begin{equation*}
\dot{\theta} = \frac{\,d\theta}{\,dx}\dot{x} + \frac{\,d\theta}{\,dy} \dot{y}
\end{equation*}
or,
\begin{equation*}
\bar{v}^{i} = \sum\limits_{j=1}^{3}\frac{\partial \bar{x}^{i}}{\partial x^{j}}{v}^{j}
\end{equation*}
The components transforming like this equation are known as the contravariant tensor components of a vector and are characterised by coordinates differential transformation or transforms like the coordinate differentials.
The tensor whose components transform like the partial derivatives of the coordinate are called covariant tensors. In the expression
\begin{equation*}
\bar{A}_{j} = \sum\limits_{i=1}^{3}\frac{\partial x^{i}}{\partial \bar{x}^{j}}{A}_{i};
\end{equation*}
where, \(\frac{\partial x^{i}}{\partial \bar{x}^{j}}\) are partial derivatives of the coordinates. If \(\psi\) expresses a velocity function, then the components of velocity in \((x,y)\) system are \(\frac{\,d\psi}{\,dx}\) and \(\frac{\,d\psi}{\,dy}\text{.}\) The transformations of these resolved parts are given as
\begin{equation*}
\frac{\,d\psi}{\,d\alpha} = \frac{\,d\psi}{\,dx} \frac{\,dx}{\,d\alpha}
+ \frac{\,d\psi}{\,dy}\frac{\,dy}{\,d\alpha}
\end{equation*}
\begin{equation*}
\frac{\,d\psi}{\,d\beta} = \frac{\,d\psi}{\,dx} \frac{\,dx}{\,d\beta}
+ \frac{\,d\psi}{\,dy} \frac{\,dy}{\,d\beta}
\end{equation*}
\begin{equation*}
\frac{\,d\psi}{\,dr} = \frac{\,d\psi}{\,dx}\frac{\,dx}{\,dr} + \frac{\,d\psi}{\,dy} \frac{\,dy}{\,dr}
\end{equation*}
and
\begin{equation*}
\frac{\,d\psi}{\,d\theta} = \frac{\,d\psi}{\,dx}\frac{\,dx}{\,d\theta}
+ \frac{\,d\psi}{\,dy}\frac{\,dy}{\,d\theta}
\end{equation*}
or,
\begin{equation*}
\bar{v}_{j} = \sum\limits_{j=1}^{3}\frac{\partial x^{i}}{\partial \bar{x}^{j}}{v}_{i}
\end{equation*}
The components which transform like this equation are called the covariant tensor components of a vector because the transformation is characterised by the partial derivatives of the coordinates or transforms like the derivatives of a scalar.
Subsubsection 3.1.1.1 Discussion
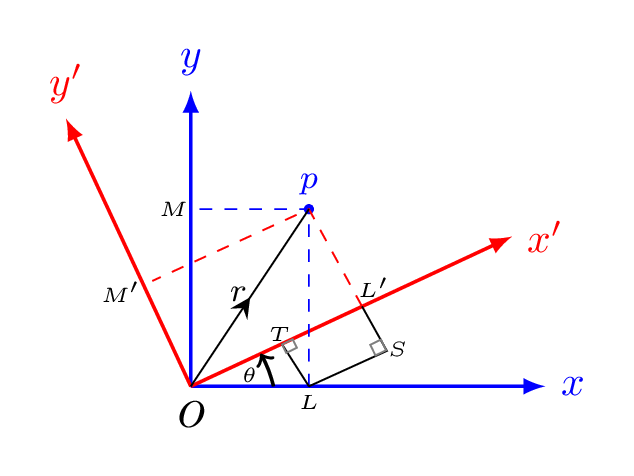
In coordinate transformation component of a tensor changes either by a contravariant manner or a covariant manner. In Figure 3.1.1.(b)
\begin{equation*}
x'=OL'= OT+TL' = OT +SL = OL\cos\theta +PL\sin\theta
\end{equation*}
\begin{equation*}
\therefore x' = x\cos\theta +y\sin\theta
\end{equation*}
\begin{equation*}
y'=PL'= PS-L'S =PS-TL = PL\cos\theta -OL\sin\theta
\end{equation*}
\begin{equation*}
\therefore y' = y\cos\theta -x\sin\theta
\end{equation*}
\begin{equation*}
\therefore \hat{i'}=\hat{i}\cos\theta +\hat{j}\sin\theta
\end{equation*}
also
\begin{equation*}
\hat{j'}=-\hat{i}\sin\theta +\hat{j}\cos\theta
\end{equation*}
also,
\begin{equation*}
\vec{r}=\hat{i'}x'+\hat{j'}y'= [\hat{i}\cos\theta +\hat{j}\sin\theta]x'+[-\hat{i}\sin\theta +\hat{j}\cos\theta]y'
\end{equation*}
\begin{equation*}
\therefore \vec{r}=\hat{i}[x'\cos\theta -y'\sin\theta] +\hat{j}[x'\sin\theta +y'\cos\theta] =\hat{i}x+\hat{i}y
\end{equation*}
In coordinate transformation, vectors remains the same but its components change. Suppose we have two types of cartesian coordinates where the basis vectors are related as \(\hat{i'}=2\hat{i}\) and \(\hat{j'}=\hat{j}\text{,}\) then \(x'= x/2\) and \(y'= y \text{.}\) For example, consider a vector \(\vec{a} = 4\hat{i}+ 3\hat{j}\) in unprimed system then \(\vec{a} = 2\hat{i'}+ 3\hat{j'}\) in the primed system, meaning if basis vectors increase the components decrease. Such type of transformation is called the contravariant transformation. Displacement, velocity, acceleration, etc. obey such type of transformation. Now consider a gradiant of scalar function
\begin{equation*}
\vec{\nabla \psi} = \frac{\partial\psi}{\partial x}\hat{i} +\frac{\partial\psi}{\partial y}\hat{j}.
\end{equation*}
Gradiant of a scalar function is a vector which represents the magnitude of maximum rate of change of the function. In previous case for a vector if \(\hat{i'}=2\hat{i}\) then it’s component \(x'= x/2\) and hence the component of the gradiant
\begin{equation*}
\frac{\partial\psi}{\partial x'}(\hat{i'})
= \frac{1}{2}\frac{\partial\psi}{\partial x}(\hat{2i})
= \frac{\partial\psi}{\partial x}(\hat{i}).
\end{equation*}
Here as basis vector increses component also has to increase by the same fasion otherwise the maximum rate of sclar changes differently in different coordinate systems. Such system where component increases as basis vector increases is called a covariant vector.
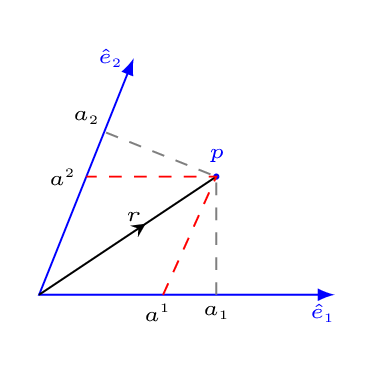
The Figure 3.1.1.(b) has shown \(a^{1}\) and \(a^{2}\) are parallel projection of a vector \(\vec{r}\) and \(a_{1}\) and \(a_{2}\) are perpendicular projection of the same vector \(\vec{r}\text{.}\) Hence
\begin{equation*}
\vec{r} = a^{1} \hat{e}_{1}+ a^{2} \hat{e}_{2}
\end{equation*}
where \(a^{1}\) and \(a^{2}\) are a contravariant vectors, and
\begin{equation*}
\vec{r} = a_{1} \hat{e}_{1}+ a_{2} \hat{e}_{2}
\end{equation*}
where \(a_{1} \) and \(a_{2}\) are covariant vectors.
