Subsection 1.2.1 Gradient of a Scalar Function
The gradient of a scalar point function \(\phi\) is defined as
\begin{align*}
\text{grad}\phi \amp =\hat{i}\frac{\partial \phi}{\partial x} + \hat{j}\frac{\partial \phi}{\partial y}
+ \hat{k}\frac{\partial \phi}{\partial z} = \left(\hat{i}\frac{\partial}{\partial x} +
\hat{j}\frac{\partial}{\partial y} + \hat{k}\frac{\partial}{\partial z}\right)\phi = \vec{\nabla\phi}
\end{align*}
where an operator \(\nabla = \hat{i}\frac{\partial}{\partial x} + \hat{j}\frac{\partial}{\partial y}
+ \hat{k}\frac{\partial}{\partial z}\) is known as \('Del'\) operator and read as a gradient or a grad, which is a vector quantity.
Subsubsection 1.2.1.1 Physical Significance of \(\vec{ \nabla \phi}\)
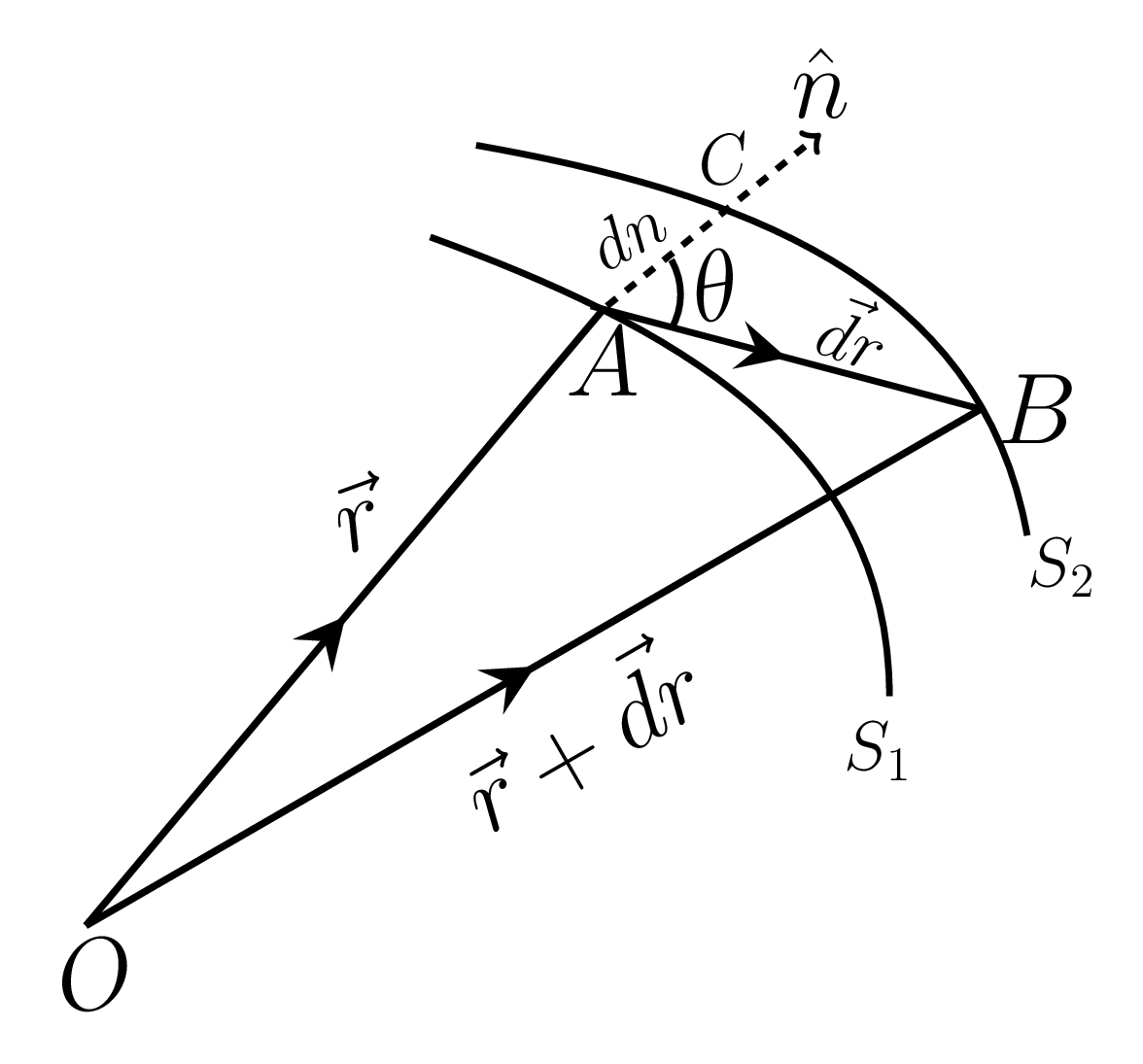
Let \(S_{1}\) and \(S_{2}\) be two level surfaces having scalar point functions \(\phi\) and \(\phi+\,d\phi\) respectively. The \(\hat{n}\) be an unit normal vector at point A and \(dn\) be the distance between the surfaces \(S_{1}\) and \(S_{2}\) along \(\hat{n}\text{.}\)
\begin{equation}
\therefore \,dn = \,dr \cos\theta = \hat{n}\cdot \vec{\,dr} \tag{1.2.1}
\end{equation}
where \(\theta\) is the angle between \(\vec{AC}\) and \(\vec{AB}\text{,}\) as shown in Figure 1.2.1. Due to a small vector \(\vec{dr}\) point B and C are very close to each other. Hence the rate of change of \(\phi\) at point A in the direction of \(\hat{n}\) is greatest and is equal to \(\frac{\partial\phi}{\partial n}\text{,}\) and the total differential,
\begin{equation}
\,d\phi = \frac{\partial\phi}{\partial n} \,dn = \frac{\partial\phi}{\partial n} \hat{n}\cdot \vec{\,dr} \tag{1.2.2}
\end{equation}
But, if \(\phi (x,y,z)\) be a function of three independent variables \((x,y,z)\) then its total differential \(\,d\phi\) is given by
\begin{equation*}
\,d \phi = \frac{\partial\phi}{\partial x} dx + \frac{\partial\phi}{\partial y} dy
+ \frac{\partial\phi}{\partial z} dz
\end{equation*}
\begin{equation}
\therefore \,d \phi = \left(\hat{i}\frac{\partial}{\partial x} + \hat{j}\frac{\partial}{\partial y}
+ \hat{k}\frac{\partial}{\partial z}\right)\phi \cdot \left(\hat{i}dx+ \hat{j}dy +\hat{k}dz\right)
= \vec{ \nabla \phi}\cdot \vec{d r} \tag{1.2.3}
\end{equation}
\begin{equation*}
\vec{ \nabla \phi}\cdot \vec{d r} = \frac{\partial\phi}{\partial n} \hat{n}\cdot \vec{dr}
\end{equation*}
\begin{equation}
\therefore \quad \vec{ \nabla \phi} = \frac{\partial\phi}{\partial n} \hat{n} \tag{1.2.4}
\end{equation}
Hence the gradient of a scalar function \(\phi\) is defined as the maximum rate of change of \(\phi\) with respect to the space variables and has the direction of that change. If \(\vec{dr}\) and \(\vec{ \nabla \phi}\) are in the same direction then \(d\phi
= \mid\vec{ \nabla \phi}\mid\cdot \mid\vec{dr}\mid\) is maximum. If \(\vec{dr}\) lies on the surface \(S_{1}\text{,}\) then \(\,d\phi = \vec{ \nabla \phi}\cdot\vec{dr} = 0\text{,}\) which represents \(\vec{dr}\) and \(\vec{ \nabla \phi}\) are perpendicular to each other, i.e., \(\vec{dr}\) lies along the direction of tangent on the given surface. Thus \(\vec{\nabla \phi}\) is normal to the surface of equation \(\phi (x,y,z) = constant\text{.}\)
Subsubsection 1.2.1.2 Directional Derivative
If \(\phi (x,y,z)\) be a scalar function at point \((x,y,z)\) in space then \(\frac{\partial\phi}{\partial x}\) is the rate of change of \(\phi\) at \((x,yz)\) in the direction of \(x\)-axis and is called as the directional derivative of \(\phi\) along \(x- axis\text{.}\) Similarly, \(\frac{\partial\phi}{\partial y}\) and \(\frac{\partial\phi}{\partial z}\) are the directional derivative of \(\phi\) along \(y\)- and \(z\)-axes, respectively. The directional derivative of \(\phi\) at A along AB is defined as \(\frac{\partial\phi}{\partial r}\) such that
\begin{equation*}
\frac{\partial\phi}{\partial r} = \frac{\partial\phi}{\partial n} \frac{\partial n}{\partial r}
= \frac{\partial\phi}{\partial n} cos\theta = \frac{\partial\phi}{\partial n} \hat{n} \cdot\hat{a}
= \vec{ \nabla \phi}\cdot \hat{a}
\end{equation*}
where \(\hat{a}\) is the unit vector along \textbf{AB}, as shown in Figure 1.2.1. Hence the directional derivative of function \(\phi\) along the given direction is the projection of a gradient of that function along this direction, i.e.,
\begin{equation*}
\frac{\partial\phi}{\partial r} = \text{projection of}\quad \vec{ \nabla \phi}\quad \text{along}\quad \hat{a}.
\end{equation*}
