Example 5.4.1.
Obtain Fourier series expansion of \(f(x) = x^{2}\) from \(-\pi\) to \(\pi\text{,}\) and deduce \(\sum\limits_{n=1}^{\infty}\frac{1}{n^{2}}\text{,}\) also find the sum of series
\begin{equation*}
\frac{1}{1^{2}} -\frac{1}{2^{2}}+\frac{1}{3^{2}}-\frac{1}{4^{2}}+\cdots.
\end{equation*}
Solution.
Let the given function is expanded in a Fourier series
\begin{equation*}
f(x) = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos nx + b_{n}\sin nx\right]
\end{equation*}
here, the function \(f(x) = x^{2}\) is an even function. Hence,
\begin{equation*}
a_{0}= \frac{2}{\pi}\int\limits_{0}^{\pi}f(x)\,dx = \frac{2}{\pi}\int\limits_{0}^{\pi}x^{2} \,dx = \frac{2}{3}\pi^{2};
\end{equation*}
\begin{equation*}
a_{n}= \frac{2}{\pi}\int\limits_{0}^{\pi}f(x) \cos nx\,dx = \frac{2}{\pi}\int\limits_{0}^{\pi} x^{2} \cos nx\,dx
\end{equation*}
\begin{equation*}
=\frac{2}{\pi}\left[x^{2}\left(\frac{\sin nx}{n}\right) -2 x \left(\frac{\cos nx}{-n^{2}}\right) + 2\left(\frac{\sin nx}{-n^{3}}\right)\right]_{0}^{\pi}
\end{equation*}
\begin{equation*}
= \frac{2}{\pi}\left[\frac{2 \pi \cos n \pi}{n^{2}}\right] = \frac{4}{n^{2}}(-1)^{n}
\end{equation*}
\(\left[\because \left(\sin nx\right)_{0}^{\pi}=0\right]\)
\begin{equation*}
\therefore x^{2} = \frac{2}{3.2}\pi^{2}+\sum\limits_{n=1}^{\infty}\frac{4}{n^{2}}(-1)^{n} \cos nx
\end{equation*}
\begin{equation}
= \frac{\pi^{2}}{3} -4\left[\frac{\cos x}{1^{2}}-\frac{\cos 2x}{2^{2}}+\frac{\cos 3x}{3^{2}}-\cdots\right] \tag{5.4.1}
\end{equation}
which is the required Fourier series expansion of the given function. The graphical representation of this function is parabolic curves as shown in figure below. 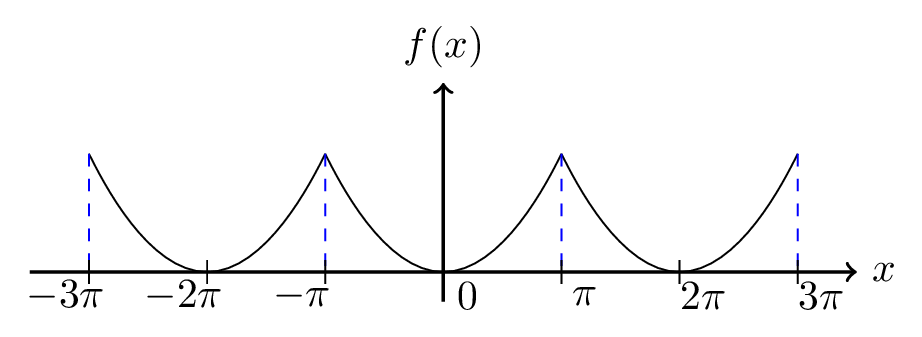

As \(x=\pm \pi\) is a point of discontinuity, the series converges to
\begin{equation*}
f(x) = \frac{1}{2}[f(-\pi+0) + f(\pi -0)] = \frac{1}{2}[\pi^{2}+\pi^{2}] = \pi^{2}.
\end{equation*}
Therefore, from eqn. (5.4.1), we have
\begin{equation*}
\pi^{2}=\frac{\pi^{2}}{3} - 4\left[-1-\frac{1}{2^{2}}-\frac{1}{3^{2}}-\cdots\right]
\end{equation*}
or,
\begin{equation*}
\frac{\pi^{2}}{6}=\sum\limits_{n=1}^{\infty}\frac{1}{n^{2}}.
\end{equation*}
Also, at the point of continuity, i.e., at \(x=0\text{,}\) we have from eqn. (5.4.1),
\begin{equation*}
0= \frac{\pi^{2}}{3} -4\left[1-\frac{1}{2^{2}}+\frac{1}{3^{2}}-\cdots\right]
\end{equation*}
or,
\begin{equation*}
1-\frac{1}{2^{2}}+\frac{1}{3^{2}}-\cdots = \frac{\pi^{2}}{12}.
\end{equation*}