Subsection 1.4.2 The Surface Integral
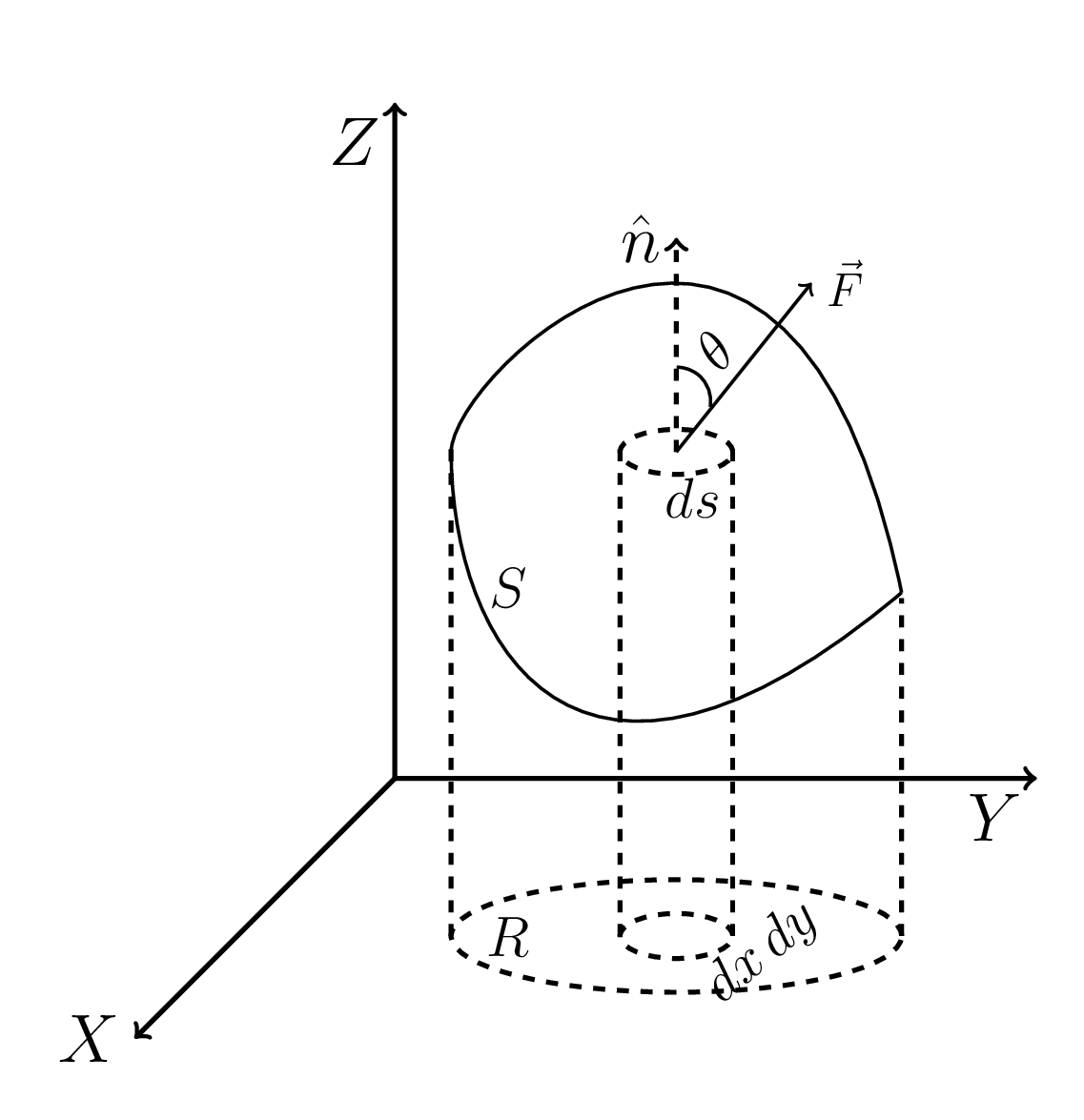
Let us consider the surface S in a vector field of function \(\vec{F}\text{,}\) as shown in Figure 1.4.2. The surface integral of a vector function \(\vec{F}\) over the surface S is defined as the integral of the components of \(\vec{F}\) along the normal to the surface. Therefore, component of \(\vec{F}\) along the normal \(=\vec{F}\cdot \hat{n}\) where \(\hat{n}\) is the unit normal vector to an element \(\,ds\) and
\begin{equation*}
\hat{n} = \frac{\text{\,grad} f}{\mid \text{\,grad} f\mid}
\end{equation*}
here, \(f\) is a scalar function and
\begin{equation*}
\vec{\nabla} f = \frac{\partial f}{\partial n}\hat{n} = \mid \vec{\nabla f}\mid \hat{n},
\end{equation*}
also
\begin{equation*}
\,ds= \frac{\,dx\,dy}{\mid \hat{n} \cdot \hat{k}\mid}.
\end{equation*}
[The projection of \(\,ds\) on the \(x~y\) plane is \(\mid \hat{n}\,ds\cdot \hat{k}\mid \quad \) or, \(\mid \hat{n}\cdot \hat{k}\mid \,ds = \,dx\,dy\)].
\(\therefore\) Surface integral of \(\vec{F}\) over S
\begin{equation*}
=\sum \vec{F}\cdot \hat{n}=\iint\limits_{s}\left(\vec{F}\cdot \hat{n}\right) ds.
\end{equation*}
Note:
\begin{equation*}
Flux = \iint\limits_{s}\left(\vec{F}\cdot \hat{n}\right) \,ds
\end{equation*}
where \(\vec{F}\) is the velocity of fluid and \((\vec{F}\cdot \hat{n})\,ds\) denotes the amount of fluid passing normally through the surface element \(\,ds\) per unit time. [If \(\iint\limits_{s}\left(\vec{F}\cdot \hat{n}\right)\,ds = 0\text{,}\) then \(\vec{F}\) is said to be a solenoidal vector].
