Skip to main content

Mathematical Methods of Physics: For Undergraduate

Sunil Karna

Subsection 4.9.1 Hermite Polynomials \(H_{n}(x)\)

Figure 4.9.1. hermite’s Polynomial
If we choose \(a_{o}=(-1)^{\frac{n}{2}}\frac{n!}{\frac{n}{2}!}\) and \(\lambda=n\) is an even integer then the series (4.9.10) is terminating which gives the even polynomial, known as Hermite Polynomial, \(H_{n}(x) \text{.}\) The term containing \(x^{n} \) in equation (4.9.10) is
\begin{equation*} (-1)^{\frac{n}{2}}\frac{n!}{\frac{n}{2}!} (-2)^{\frac{n}{2}}\frac{n(n-2)\cdots(n-n+2)}{n!}x^{n} \end{equation*}
\begin{equation*} =(-1)^{\frac{n}{2}}\frac{n!}{\frac{n}{2}!} (-1)^{\frac{n}{2}}(2)^{\frac{n}{2}}\frac{\frac{n}{2}(\frac{n}{2}-2)\cdots1}{n!}2^{\frac{n}{2}}x^{n} \end{equation*}
\begin{equation*} =(-1)^{n}2^{n}\frac{(\frac{n}{2})!}{(\frac{n}{2})!}x^{n}=(2x)^{n}. \end{equation*}
The term containing \(x^{n-2}\) is
\begin{equation*} (-1)^{\frac{n}{2}}\frac{n!}{\frac{n}{2}!} (-2)^{\frac{n-2}{2}}\frac{n(n-2)\cdots(n-n+4)}{(n-2)!}x^{n-2} \end{equation*}
\begin{equation*} = (-1)^{\frac{n}{2}} \frac{n(n-1)!(n-2)}{\frac{n}{2}!} (-1)^{\frac{n}{2}} (2)^{\frac{n-2}{2}} \end{equation*}
\begin{equation*} \times (-1)^{-1}\frac{\frac{n}{2}(\frac{n}{2}-2)\cdots2\cdot1}{1!(n-2)!}2^{\frac{n}{2}}(2)^{\frac{n-2}{2}}x^{n-2} \end{equation*}
\begin{equation*} =-\frac{n(n-1)}{1!} 2^{n-2}x^{n-2}=-\frac{n(n-1)}{1!}(2x)^{n-2} \end{equation*}
and so on. Therefore, the Hermite Polynomial \(H_{n}(x)\) is defined as
\begin{equation*} H_{n}(x)=\left[(2x)^{n}-\frac{n(n-1)}{1!}(2x)^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2!}(2x)^{n-4} \right. \end{equation*}
\begin{equation*} \left.+\cdots+(-1)^{r}\frac{n(n-1)(n-2)\cdots(n-2r+1)}{r!}(2x)^{n-2r}\right. \end{equation*}
\begin{equation} \left. +\cdots+(-1)^{r}\frac{n!}{(\frac{n}{2})!}\right]\tag{4.9.12} \end{equation}
Similarly, equation (4.9.9) reduces to a polynomial if \(\lambda=m \) is an odd integer. Let’s choose
\begin{equation*} a_{o}=(-1)^{\frac{m-1}{2}}\frac{(m+1)!}{(\frac{m+1}{2})!}, \end{equation*}
then the term containing \(x^{m}\) in the equation (4.9.9) is
\begin{equation*} (-1)^{\frac{m-1}{2}}\frac{(m+1)!}{(\frac{m+1}{2})!}(-2)^{\frac{m-1}{2}}\frac{(m-1)(m-3)\cdots(m-m+1+1)}{m!}x^{m} \end{equation*}
\([\because m=2r+1]\)
\begin{equation*} =(-1)^{m-1}(2)^{\frac{m-1}{2}}\frac{(m+1)(m-1)(m-3)\cdots2}{(\frac{m+1}{2})!}x^{m} \end{equation*}
\begin{equation*} =2^{(\frac{m-1}{2})}\frac{(\frac{m+1}{2})(\frac{m-1}{2})\cdots1}{(\frac{m+1}{2})!}2^{(\frac{m+1}{2})}x^{m} \end{equation*}
\begin{equation*} =2^{m}x^{m}=(2x)^{m} \end{equation*}
and so on. Hence, we have the Hermite polynomia for odd integer is
\begin{equation*} H_{m}(x)=\left[(2x)^{m}-\frac{m(m-1)}{1!}(2x)^{m-2}+\cdots\right. \end{equation*}
\begin{equation*} \left.+(-1)^{r}\frac{m(m-1)\cdots(m-2r+1)}{r!}(2x)^{m-2r}+\cdots\right. \end{equation*}
\begin{equation} \left.+(-1)^{(\frac{m-1}{2})}\frac{(m+1)!}{(\frac{m+1}{2})!}x\right]\tag{4.9.13} \end{equation}
From equations (4.9.12) and (4.9.13), we get -
\begin{equation*} H_{n}(0)=(-1)^{n}\frac{n!}{(\frac{n}{2})!} \end{equation*}
where \(n\) is even and \(H_{m}(0)\) where \(m\) is odd. For particulars, we have
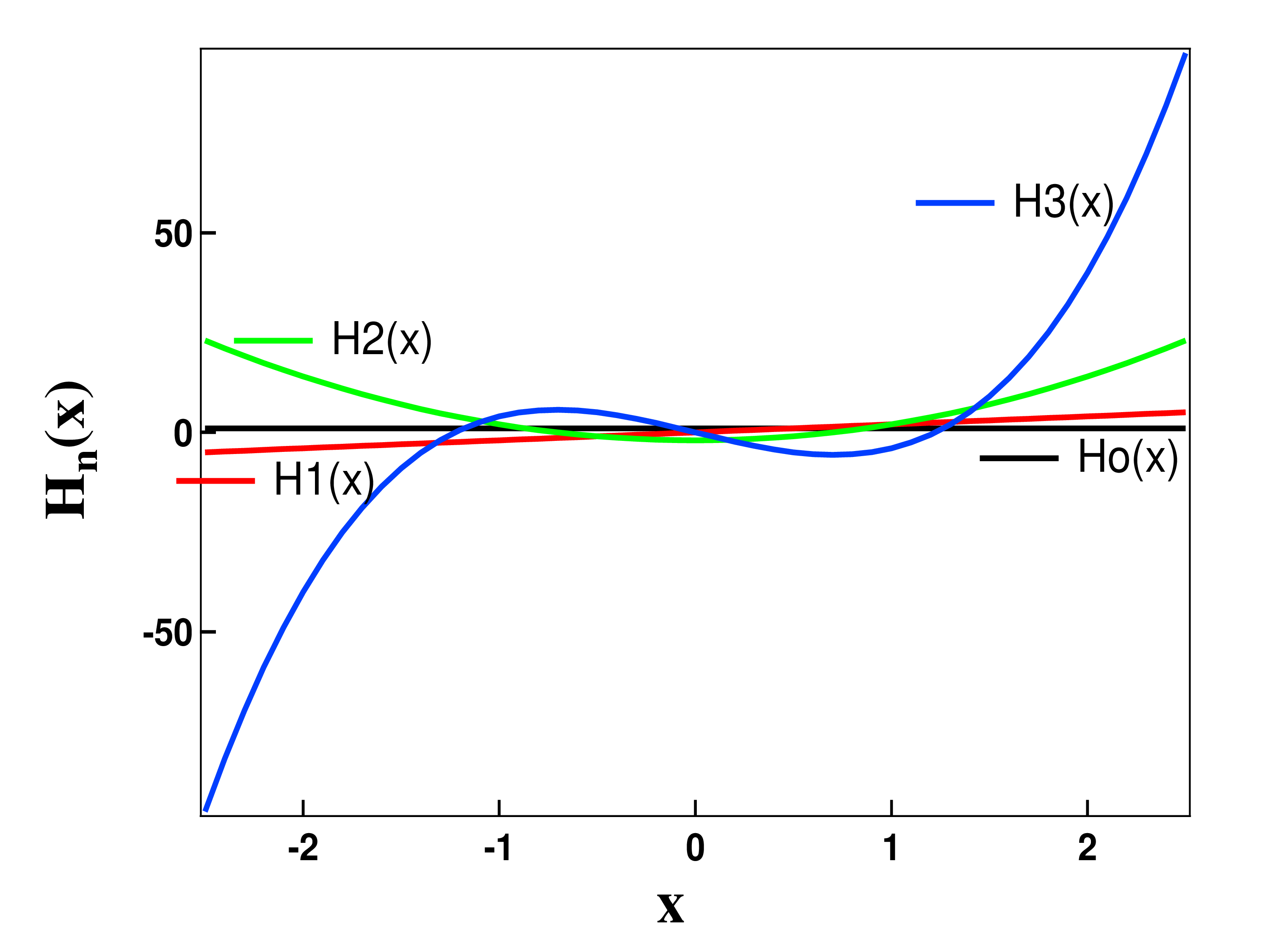
\begin{equation*} H_{o}(x)=1, \quad H_{1}(x)=2x,\quad H_{2}(x)=4x^{2}-2, \quad H_{3}(x)=8x^{3}-12, \end{equation*}
\begin{equation*} H_{4}(x)=16x^{4}-48x^{2}+12, \end{equation*}
and so on. In general
\begin{equation*} H_{n}(x)=\sum\limits_{r=0}^{N}(-1)^{r}\frac{n!}{r!(n-2r)!}(2x)^{n-2r} \end{equation*}
where
\begin{equation*} N=\begin{cases} \frac{n}{2}, & \text{if n is even}\\ \frac{n-1}{2}, & \text{if n is odd}. \end{cases} \end{equation*}
The graph of these functions is shown in figure Figure 4.9.1.

Pythone Code:.

import math
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import hermite
def HERMITE(X,N):
HER = hermite(N)
sn = HER(X)
return sn
x = np.linspace(-2.5,2.5,1000)
for n in np.arange(0,5,1):
y = HERMITE(x,n)
plt.plot(x, y, label=r’$H_{}(x)$’.format(n))
plt.title("Hermite Polynomials")
plt.xlabel("x")
plt.ylabel(r’$H_n(x)$’)
plt.legend(loc=’lower right’)
plt.show()

Subsubsection 4.9.1.1 Generating Function for \(H_{n}(x)\)

Hermite polynomial \(H_{n}(x)\) is the coefficient of \(\frac{z^{n}}{n!}\) in the expansion of \(e^{2zx-z^{2}} \) i.e.,
\begin{equation} e^{2zx-z^{2}}=\sum_{n=0}^{\infty} \frac{z^{n}}{n!}H_{n}(x) \tag{4.9.14} \end{equation}

Proof.

We have
\begin{equation*} e^{2zx-z^{2}}=e^{2zx}\cdot e^{-z^{2}} \end{equation*}
\begin{equation*} =\left[1+2zx+\frac{(2x)^{2}}{2!}z^{2}+\cdots+\frac{(2x)^{r}}{r!}z^{r}+\cdots\right] \end{equation*}
\begin{equation*} \cdot\left[1-\frac{z^{2}}{1!}+\frac{(z^{2})^{2}}{2!}-\cdots+(-1)^{s}\frac{z^{2s}}{s!}+\cdots\right] \end{equation*}
\begin{equation*} =\sum_{r=0}^{\infty} \frac{(2x)^{r}}{r!}z^{r}\cdot\sum_{s=0}^{\infty} (-1)^{s}\frac{(z)^{2s}}{s!} \end{equation*}
\begin{equation} =\sum_{r=0}^{\infty}\sum_{s=0}^{\infty}(-1)^{s}\frac{(2x)^{r}}{r!s!} z^{r+2s}\tag{4.9.15} \end{equation}
for fixed value of \(s\text{,}\) (as \(r\) in the general term of \(H_{n}(x)\)) the coefficient of \(z^{n}\) is obtained by putting \(r+2s=n\) or, \(r=n-2s\)
\begin{equation*} \therefore e^{2zx-z^{2}}=\sum_{s=0}^{\infty}\frac{(-1)^{s}(2x)^{n-2s}}{s!(n-2s)!}z^{n} \end{equation*}
Now, we know that since \(r \geq 0\text{,}\) we must have \(n-2s \geq 0 \) or, \(s\leq \frac{n}{2} \text{.}\) Thus, if \(n\) is even \(s\) varies from 0 to \(\frac{n}{2}\) and when \(n\) is odd \(s\) varies from 0 to \(\frac{n-1}{2}\text{.}\) Hence, the coefficient of \(z^{n}\)
\begin{equation*} =\sum_{s=0}^{\infty}\frac{(-1)^{s}(2x)^{n-2s}}{s!(n-2s)!}\frac{n!}{n!}=\frac{H_{n}(x)}{n!} \end{equation*}
Hence,
\begin{equation} e^{2zx-z^{2}}=\sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}z^{n}\tag{4.9.16} \end{equation}
The function \(e^{2zx-z^{2}} \) is thus said to be the generating function of Hermite polynomials.

Subsubsection 4.9.1.2 Rodrigue’s Formula for Hermite Polynomials

\begin{equation*} H_{n}(x)=(-1)^{n}e^{x^{2}}\frac{d^{n}}{dx^{n}}(e^{-x^{2}}) \end{equation*}
is the Rodrigue’s formula for Hermite polynomials.

Proof.

We know that
\begin{equation} e^{2zx-z^{2}}= e^{x^{2}-(z-x)^{2}}=\sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}z^{n}\tag{4.9.17} \end{equation}
Differentiating \(n\) times w. r. t. \(z\text{,}\) we get -
\begin{equation} e^{x^{2}}\frac{d^{n}}{dx^{n}}[e^{-(z-x)^{2}}]= H_{n}(x)+H_{n+1}(x)z+\cdots\tag{4.9.18} \end{equation}
But, we have
\begin{equation*} \frac{\,d}{\,dz}[e^{-(z-x)^{2}}]=-2(z-x)e^{-(z-x)^{2}} \end{equation*}
and
\begin{equation*} \frac{\,d}{\,dx}[e^{-(z-x)^{2}}]=+2(z-x)e^{-(z-x)^{2}} \end{equation*}
or,
\begin{equation*} \lim\limits_{z\to 0}\frac{\,d}{\,dz}[e^{-(z-x)^{2}}]=2xe^{-x^{2}}=(-1)^{1}\lim\limits_{z\to 0}\frac{d}{dx}[e^{-(z-x)^{2}}] \end{equation*}
similarly,
\begin{equation*} \lim\limits_{z\to 0}\frac{d^{2}}{dz^{2}}[e^{-(z-x)^{2}}]=(-1)^{2}\lim\limits_{z\to 0}\frac{d^{2}}{dx^{2}}[e^{-(z-x)^{2}}] \end{equation*}
and so on. In general,
\begin{equation*} \lim\limits_{z\to 0}\frac{d^{n}}{dz^{n}}[e^{-(z-x)^{2}}] \end{equation*}
\begin{equation} =(-1)^{n}\lim\limits_{z\to 0}\frac{d^{n}}{dx^{n}}[e^{-(z-x)^{2}}]=(-1)^{n}\frac{d^{n}}{dx^{n}}[e^{-x^{2}}]\tag{4.9.19} \end{equation}
Hence from equation (4.9.18), we have
\begin{equation*} \lim\limits_{z\to 0}e^{x^{2}}\frac{d^{n}}{dz^{n}}[e^{-(z-x)^{2}}]=H_{n}(x) \end{equation*}
\begin{equation*} = e^{x^{2}}\lim\limits_{z\to 0}\frac{d^{n}}{dz^{n}} [e^{-(z-x)^{2}}]= e^{x^{2}}(-1)^{n}\frac{d^{n}}{dx^{n}}e^{-x^{2}} \end{equation*}
[from equation (4.9.19)]
\begin{equation} \therefore H_{n}(x)=(-1)^{n} e^{x^{2}}\frac{d^{n}}{dx^{n}}[e^{-x^{2}}] \tag{4.9.20} \end{equation}
This is differential form of Hermite polynomial, which gives
\begin{equation*} H_{o}(x)=1, H_{1}(x)=2x, H_{2}(x)=4x^{2}-2, \end{equation*}
and so on.

Subsubsection 4.9.1.3 Recurrence Relation for Hermite Polynomials

  1. \begin{equation*} 2n H_{n-1}(x) = H'_{n}(x) \end{equation*}

    Proof.

    We know that
    \begin{equation} e^{2zx-z^{2}}=\sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}z^{n}\tag{4.9.21} \end{equation}
    Differentiating w. r. to \(x\text{,}\) we get -
    \begin{equation} 2z e^{2zx-z^{2}}=\sum_{n=0}^{\infty}\frac{H'_{n}(x)}{n!}z^{n}\tag{4.9.22} \end{equation}
    or,
    \begin{equation*} 2z\frac{H_{n}(x)}{n!}z^{n}=\sum_{n=0}^{\infty}\frac{H'_{n}(x)}{n!}z^{n} \end{equation*}
    or,
    \begin{equation*} 2\frac{H_{n}(x)}{n!}z^{n+1}=\sum_{n=0}^{\infty}\frac{H'_{n}(x)}{n!}z^{n} \end{equation*}
    Equating the coefficients of \(z^{n}\) on both sides, we get -
    \begin{equation*} 2\frac{H_{n-1}}{(n-1)!}=\frac{H'_{n}}{n!} \end{equation*}
    or,
    \begin{equation*} 2\frac{H_{n-1}}{(n-1)!}=\frac{H'_{n}}{n(n-1)!} \end{equation*}
    or,
    \begin{equation*} 2n H_{n-1}=H'_{n} \end{equation*}
  2. \begin{equation*} 2x H_{n}= 2nH_{n-1}+H_{n+1} \end{equation*}

    Proof.

    We know that
    \begin{equation} e^{2zx-z^{2}}=\sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}z^{n}\tag{4.9.23} \end{equation}
    Differentiating w. r. to \(z\text{,}\) we get -
    \begin{equation*} (2x-2z) e^{2zx-z^{2}}=\sum_{n=0}^{\infty}n\frac{H_{n}(x)}{n!}z^{n-1} \end{equation*}
    or,
    \begin{equation*} 2x\frac{H_{n}(x)}{n!}z^{n}-2\sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}z^{n+1} \end{equation*}
    \begin{equation} =\sum_{n=0}^{\infty}\frac{H_{n}(x)}{(n-1)!}z^{n-1}\tag{4.9.24} \end{equation}
    Equating the coefficient of \(z^{n}\) on both sides, we get -
    \begin{equation*} 2x\frac{H_{n}}{(n)!}-2\frac{H_{n-1}}{(n-1)!}=\frac{H_{n+1}}{(n)!} \end{equation*}
    or,
    \begin{equation*} 2x\frac{H_{n}}{n}-2H_{n-1}=\frac{H_{n+1}}{n} \end{equation*}
    or,
    \begin{equation*} 2xH_{n}=2nH_{n-1}+H_{n+1} \end{equation*}
  3. \begin{equation*} H'_{n}=2xH_{n}-H_{n+1} \end{equation*}

    Proof.

    We have
    \begin{equation} 2n H_{n-1}=H'_{n}\tag{4.9.25} \end{equation}
    [from relation 1.] and
    \begin{equation} 2x H_{n}=2nH_{n-1}+H_{n+1}\tag{4.9.26} \end{equation}
    [from relation 2.] Substituting equation (4.9.25) in equation (4.9.26), we get -
    \begin{equation*} H'_{n}=2xH_{n}-H_{n+1} \end{equation*}
  4. \begin{equation*} H''_{n}-2xH'_{n}+2nH_{n}=0. \end{equation*}

    Proof.

    Differentiating relation 3. w. r. to \(x\) we get -
    \begin{equation} H''_{n}=2H_{n}+2xH'_{n}-H'_{n+1}\tag{4.9.27} \end{equation}
    From relation 1, we have -
    \begin{equation*} 2nH_{n-1}=H'_{n} \end{equation*}
    put, \(n=n+1\) we get -
    \begin{equation} 2(n+1)H_{n}=H'_{n+1}\tag{4.9.28} \end{equation}
    Substituting equation (4.9.28) in equation (4.9.27), we get -
    \begin{equation*} H''_{n}=2H_{n}+2xH'_{n}-2(n+1)H_{n} \end{equation*}
    \begin{equation*} H''_{n}-2xH'_{n}+2nH_{n}=0. \end{equation*}

Subsubsection 4.9.1.4 Orthogonality of Hermite Polynomials

\begin{equation*} \int\limits_{-\infty}^{\infty}e^{-x^{2}}H_{m}(x) H_{n}(x)\,dx =2^{n}n!\sqrt{\pi}\delta_{m,n} \end{equation*}
where
\begin{equation*} \delta_{m,n}= \begin{cases} 1, & \text{for}\quad m=n\\ 0, & \text{for}\quad m \neq n \end{cases} \end{equation*}

Proof.

We know that
\begin{equation} e^{2tx-t^{2}}=\sum_{m=0}^{\infty}\frac{H_{m}(x)}{m!}t^{m}\tag{4.9.29} \end{equation}
and
\begin{equation} e^{2sx-s^{2}}=\sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}s^{n}\tag{4.9.30} \end{equation}
Multiplying equations (4.9.29) and (4.9.30), we get -
\begin{equation*} e^{2tx-t^{2}}\times e^{2sx-s^{2}}= \sum_{m=0}^{\infty}\frac{H_{m}(x)}{m!}t^{m} \times \sum_{n=0}^{\infty}\frac{H_{n}(x)}{n!}s^{n} \end{equation*}
or,
\begin{equation*} \sum_{m,n=0}^{\infty}\frac{H_{m}(x)}{m!}\frac{H_{n}(x)}{n!}t^{m}s^{n}=e^{2tx-t^{2}+2sx-s^{2}} \end{equation*}
\begin{equation} =e^{2x(t+s)-(t^{2}+s^{2})}\tag{4.9.31} \end{equation}
Now multiplying equation (4.9.31) by \(e^{-x^{2}}\) on both sides and integrating w. r. t. ’x’ from \(-\infty\) to \(\infty \text{,}\) we get -
\begin{equation*} \sum_{m,n=0}^{\infty}\left[\int\limits_{-\infty}^{\infty}e^{-x^{2}}H_{m}(x)H_{n}(x)\,dx\right]\frac{t^{m}s^{n}}{m!n!} =\int\limits_{-\infty}^{\infty}e^{-x^{2}+2x(t+s)-(t^{2}+s^{2})}\,dx \end{equation*}
\begin{equation*} =\int\limits_{-\infty}^{\infty}e^{-x^{2}+2x(t+s)-(t+s)^{2}}\cdot e^{2ts}\,dx \end{equation*}
putting \([x-(t+s)]=y\) so that \(\,dx=\,dy\text{.}\)
\begin{equation*} =e^{2ts}\int\limits_{-\infty}^{\infty}e^{-y^{2}}\,dy =e^{2ts}\sqrt{\pi} \hspace{1cm} \left[\because \int\limits_{-\infty}^{\infty}e^{-y^{2}}\,dy=\sqrt{\pi}\right] \end{equation*}
\begin{equation} =\sqrt{\pi}\sum_{n=0}^{\infty}\frac{(2ts)^{n}}{n!}=\sum_{n=0}^{\infty}\sqrt{\pi}\frac{2^{n}t^{n}s^{n}}{n!}\tag{4.9.32} \end{equation}
The RHS of series contains only the terms having equal powers of \('t'\) and \('s'\text{.}\) Therefore the coefficient of \(t^{n}s^{n}\) provided \(m \neq n\) will be zero. Hence equating the coefficient of \(t^{m}s^{n}\) on both sides of equation (4.9.32), we get -
\begin{equation} \int\limits_{-\infty}^{\infty}e^{-x^{2}}H_{m}(x)H_{n}(x)\,dx =0 \text{when} \quad m \neq n\tag{4.9.33} \end{equation}
and
\begin{equation} \int\limits_{-\infty}^{\infty}e^{-x^{2}}H_{m}(x)H_{n}(x)\,dx =\sqrt{\pi} 2^{n}n! \quad \text{when}\quad m = n\tag{4.9.34} \end{equation}
Hence from equations (4.9.33) and (4.9.34), we have
\begin{equation} \int\limits_{-\infty}^{\infty}e^{-x^{2}}H_{m}(x)H_{n}(x)\,dx =2^{n}\sqrt{\pi} n! \delta_{m,n}; \tag{4.9.35} \end{equation}
where,
\begin{equation*} \delta_{m,n}= \begin{cases} 1, & \text{for}\quad m=n\\ 0, & \text{for}\quad m \neq n \end{cases} \end{equation*}
PrevTopNext