Subsection 3.1.3 Transformation of Coordinates
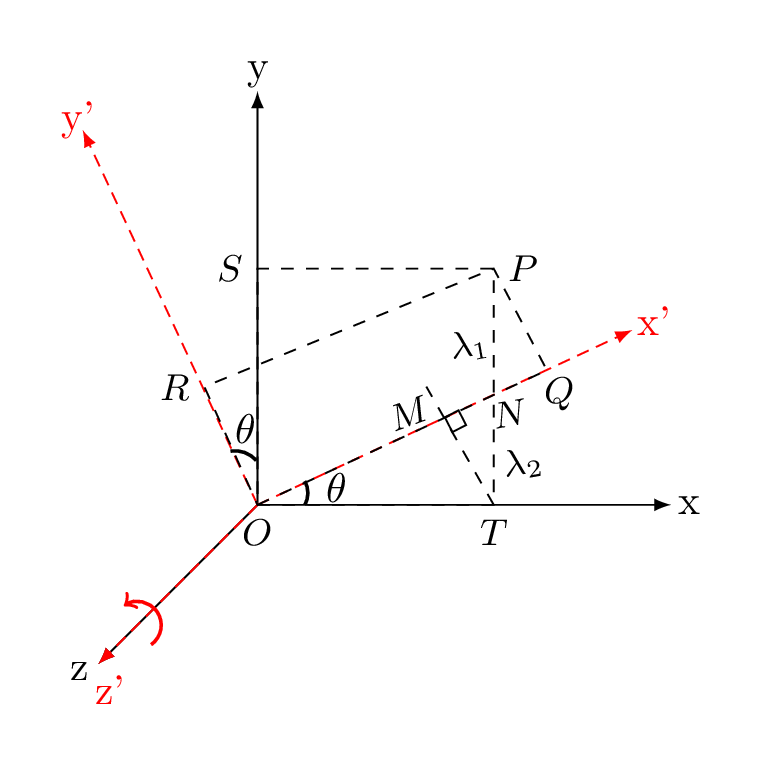
Let \((x,y,z)\) and \((x', y', z')\) are the coordinates of point P in prime and unprimed systems, respectively as shown in Figure 3.1.2. Now, if the frame rotates about \(z\) axis, then their relations are given as
\begin{equation*}
x' = OQ = OM + MN + NQ
\end{equation*}
\begin{equation*}
= x\cos\theta + \lambda_{2}\sin\theta +\lambda_{1}\sin\theta
= x\cos\theta + (\lambda_{1}+\lambda_{2})\sin\theta
\end{equation*}
\begin{equation}
\therefore \quad x^{'} = x\cos\theta + y \sin\theta\tag{3.1.10}
\end{equation}
and
\begin{equation*}
y^{'} = OR = QP = \lambda_{1} \sin(90^{o}-\theta)
\end{equation*}
\begin{equation*}
= \lambda_{1} \cos\theta
= (y-\lambda_{2})\cos\theta
=y \cos\theta-\lambda_{2}\cos\theta
= y \cos\theta -TM
\end{equation*}
\begin{equation}
\therefore y^{'} = y \cos\theta -x\sin\theta\tag{3.1.11}
\end{equation}
If we replace \(x'\) by \(x^{'}_{1}\text{,}\) \(y'\) by \(x^{'}_{2}\text{,}\) \(x\) by \(x_{1}\) and \(y\) by \(x_{2}\text{,}\)
\begin{equation*}
x'_{1} = x_{1}\cos\theta + x_{2} \sin\theta
\end{equation*}
and
\begin{equation*}
x'_{2} = -x_{1}\sin\theta + x_{2} \cos\theta
\end{equation*}
or,
\begin{equation*}
x'_{1} = x_{1}a_{11} + x_{2} a_{12}
\end{equation*}
and
\begin{equation*}
x'_{2} = -x_{1}a_{21} + x_{2} a_{22}
\end{equation*}
or,
\begin{equation}
x'_{i} = \sum\limits_{j=1}^{2}a_{ij}x_{j}\quad [i=1,2]\tag{3.1.12}
\end{equation}
If we take rotation in three dimensional space, then the transformation of the coordinates can be written as
\begin{equation}
x'_{i} = \sum\limits_{j=1}^{3}a_{ij}x_{j} \quad [i=1,2,3]\tag{3.1.13}
\end{equation}
where \(a_{ij} = \cos(x'_{i}, x_{j})\) [for \(i,j = 1,2,3\)], the direction cosines of prime components w.r.t. unprimed. or, simply,
\begin{equation}
x'_{i} = a_{ij}x_{j}\tag{3.1.14}
\end{equation}
and
\begin{equation}
x'_{j} = a_{ij}x_{i}\tag{3.1.15}
\end{equation}
when a suffix is repeated in expressions like (3.1.14) and (3.1.15), they denote the sum of three quantities by giving a dummy index of values 1, 2, and 3. Hence,
\begin{equation*}
x'_{1} = a_{11}x_{1} + a_{21}x_{2} + a_{31}x_{3} = \lambda_{1}x_{1} + m_{1}x_{2}+n_{1}x_{3}
\end{equation*}
\begin{equation*}
and, x'= \lambda_{1}x + m_{1}y+n_{1}z
\end{equation*}
where \(\lambda_{1}\text{,}\) \(m_{1}\text{,}\) \(n_{1}\) are directions cosines of \(OX'{,} OY'{,} OZ'\) in \(X{,}Y{,}Z\) system.
