From right - hand side of the above equation, we have -
\begin{equation}
\iiint\limits_{V}(\vec{\nabla}\cdot \vec{F})\,dV=\iiint\limits_{V}\left[\frac{\partial F_{x}}{\partial x}+\frac{\partial F_{y}}{\partial y}
+\frac{\partial F_{z}}{\partial z}\right] \,dV\tag{1.4.1}
\end{equation}
Since the theorem is valid for any shape. We chose parallelopiped of volume V enclosed by the surface S, as showh in the figure Figure 1.4.4.
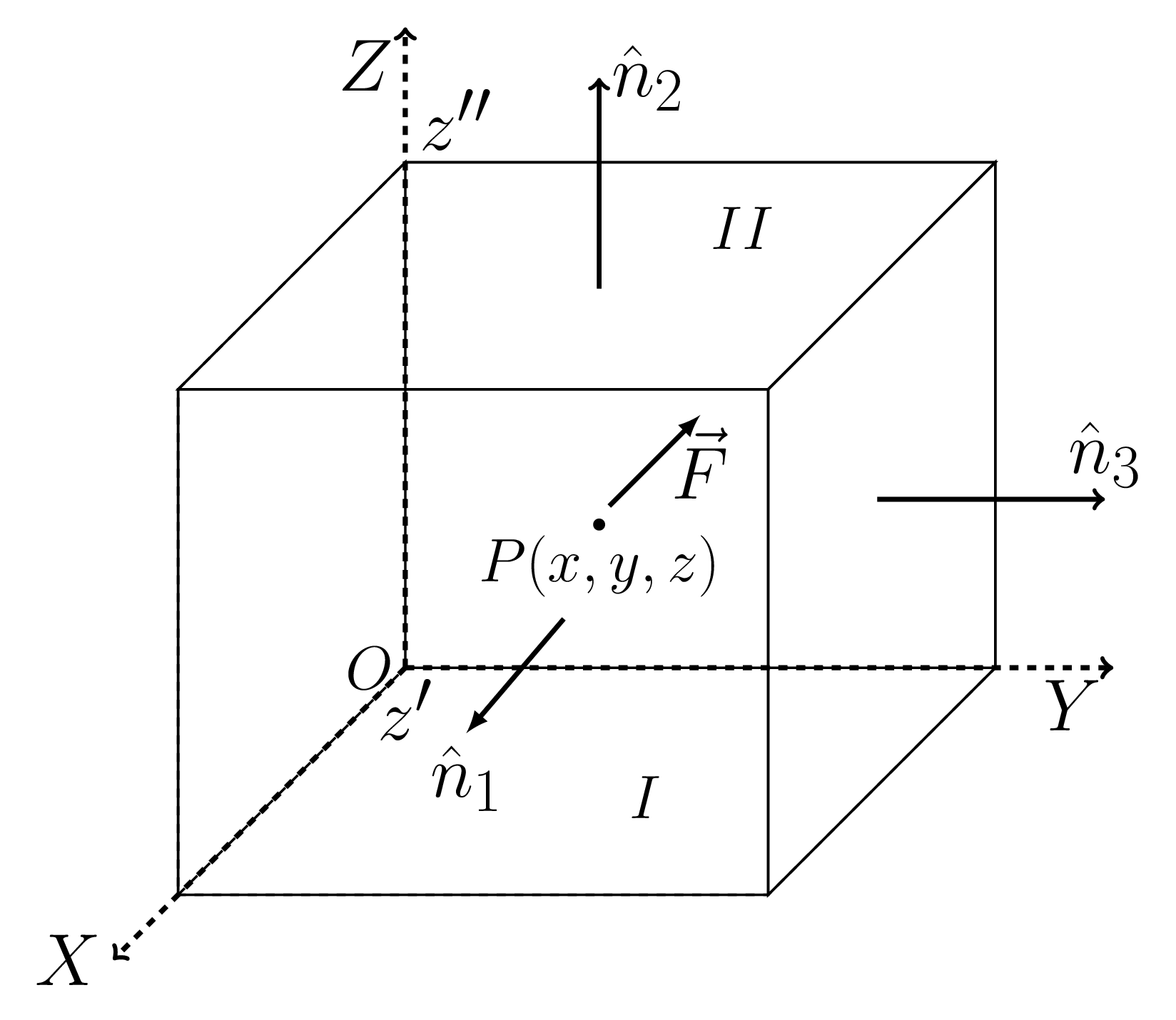
From eqn. (1.4.1) let us first evaluate -
\begin{equation*}
\iiint\limits_{V}\frac{\partial F_{z}}{\partial z}\,dx\,dy\,dz \quad \text{from z' to z''.}
\end{equation*}
That is,
\begin{equation*}
\iiint\limits_{z'}^{z"}\frac{\delta F_{z}}{\delta z}\,dx\,dy\,dz
\end{equation*}
[value of \(\vec{F}\) along z axis is \(F_{z}(x,y,z)\)]
\begin{equation*}
\therefore \hspace{2pt} \iint\limits_{S}[F_{z}(x,y,z")-F_{z}(x,y,z')\,dx\,dy]
\end{equation*}
\begin{equation}
=\iint\limits_{S_{2}}F_{z}(x,y,z")\,dx\,dy-\iint\limits_{S_{1}}F_{z}(x,y,z')\,dx\,dy\tag{1.4.2}
\end{equation}
But, \(\hat{n_{1}}\cdot\hat{k}\,dS_{1}=-\,dx\,dy\) (bottom surface ) and \(\hat{n_{2}}\cdot\hat{k}dS_{2}=\,dx\,dy\) (top).
Hence from eqn. (1.4.2), we get-
\begin{equation*}
\iiint\limits_{z'}^{z"}\frac{\partial F_{z}}{\partial z}\,dx\,dy\,dz
=\iint\limits_{S_{2}}F_{z}(x,y,z")\hat{n_{2}}\cdot\hat{k}\,dS_{2}+\iint\limits_{S_{1}}F_{z}(x,y,z')\hat{n_{1}}\cdot\hat{k}dS_{1}
\end{equation*}
\begin{equation}
\therefore\quad \iiint\limits_{z'}^{z"}\frac{\partial F_{z}}{\partial z}\,dx\,dy\,dz = \mathop{\vcenter{\huge\unicode{x222F}\,}}_{S} F_{z}\hat{k} \cdot \hat{n} \,dS \tag{1.4.3}
\end{equation}
where surface integrals of the other sides are zero because \(\hat{k}\) is perpendicular to the surfaces \(\,dS_{3},\,dS_{4},\,dS_{5},\,dS_{6}\text{.}\) Similarly, we can show that
\begin{equation}
\iiint\limits_{V}\frac{\partial F_{x}}{\partial x}dxdydz = \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} F_{x}\hat{i} \cdot \hat{n} \,dS \tag{1.4.4}
\end{equation}
and
\begin{equation}
\iiint\limits_{V}\frac{\partial F_{y}}{\partial y}\,dx\,dy\,dz = \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} F_{y}\hat{j} \cdot \hat{n} \,dS \tag{1.4.5}
\end{equation}
Adding eqns. (1.4.3)–(1.4.5), we get-
\begin{equation*}
\iiint\limits_{V}(\vec{\nabla}\cdot \vec{F})\,dV
= \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} (F_{x}\hat{i}+F_{y}\hat{j}+F_{z}\hat{k}) \cdot \hat{n} \,dS
= \mathop{\vcenter{\huge\unicode{x222F}\,}}\limits_{S} \vec{F}\cdot\vec{\,dS}
\end{equation*}
