\begin{equation*}
\oint\limits_{C}\vec{F}\cdot\vec{\,dr}=\iint\limits_{S} \left(\vec{\nabla} \times \hat{i}F_{x}+\vec{\nabla} \times \hat{j}F_{y}+\vec{\nabla} \times \hat{k}F_{z}\right)\cdot\hat{n}\,dS
\end{equation*}
Let us first prove,
\begin{equation}
\iint_{S} \left[\vec{\nabla} \times \hat{i}F_{x}\right]\cdot\hat{n}\,dS = \iint\limits_{S} \left[\frac{\partial F_{x}}{\partial z}\hat{n}\cdot\hat{j}-\frac{\partial F_{x}}{\partial y}\hat{n}\cdot\hat{k}\right]\,dS\tag{1.4.6}
\end{equation}
\begin{equation*}
\left[\because \vec{\nabla} \times \hat{i}F_{x} = \left(\hat{i}\frac{\partial}{\partial x}+\hat{j}\frac{\partial}{\partial y}+\hat{k}\frac{\partial}{\partial z}\right)\times \hat{i} F_{x}=-\hat{k}\frac{\partial F_{x}}{\partial y}+\hat{j}\frac{\partial F_{x}}{\partial z}\right]
\end{equation*}
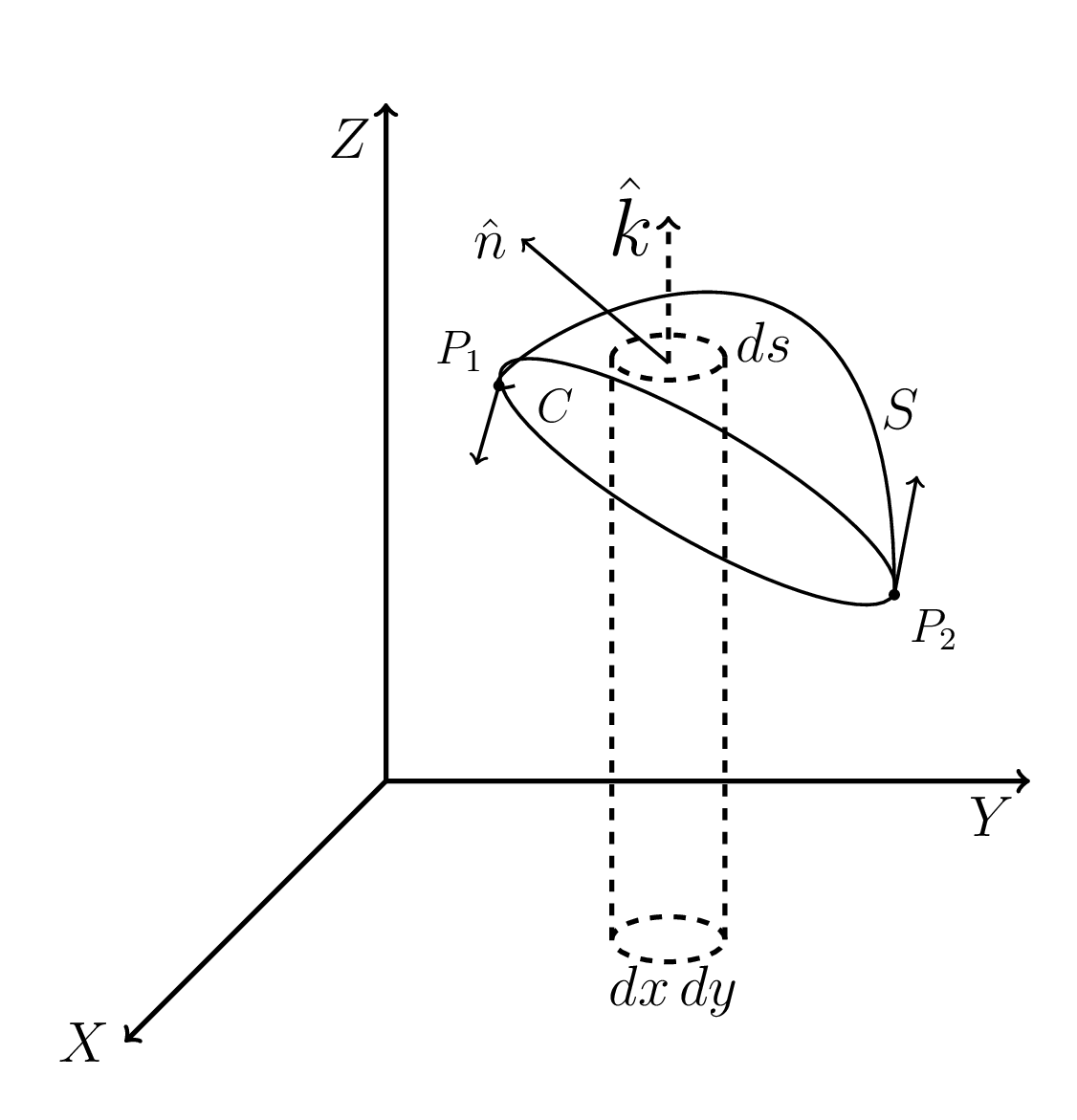
Let \(f(x,y,z)\) be the equation of surface S and its projection on x-y plane is
\begin{equation}
\hat{n}\cdot\hat{k}\,dS = \,dx\,dy\tag{1.4.7}
\end{equation}
but on the surface S, we have \(F_{x}(x,y,z)=F_{x}[f(x,y),y,z]\text{.}\)
\begin{equation}
\therefore \,dF_{x}= \frac{\partial F_{x}}{\partial y}\,dy+\frac{\partial F_{x}}{\partial z}\,dz\tag{1.4.8}
\end{equation}
and \(\vec{\,dr}= \,dy\hat{j}+\,dz\hat{k}\text{;}\) where \(\vec{\,dr}\) is tangent to the surface ds at point A and is perpendicular to \(\hat{n}\text{.}\)
\begin{equation*}
\therefore \vec{\,dr}\cdot\hat{n} = 0 =\,dy\hat{n}\cdot\hat{j} +\,dz\hat{n}\cdot\hat{k}
\end{equation*}
or,
\begin{equation*}
\hat{n}\cdot\hat{j}= \frac{\,dz}{\,dy}\hat{n}\cdot\hat{k} = -\frac{\,dz}{\,dy}\left(\frac{\,dx\,dy}{\,dS}\right)
\end{equation*}
\begin{equation}
\therefore \hat{n}\cdot\hat{j}\,dS=-\,dx\,dz \tag{1.4.9}
\end{equation}
putting the values of eqns. (1.4.7)–(1.4.9) in eqn. (1.4.6), we get-
\begin{equation*}
\iint\limits_{S} \left[\vec{\nabla} \times \hat{i}F_{x}\right]\cdot\hat{n}\,dS = -\iint\limits_{S} \left[\frac{\partial F_{x}}{\partial z}\,dz +\frac{\partial F_{x}}{\partial y}\,dy\right]\,dx
\end{equation*}
\begin{equation*}
=\int \,dx\int\limits_{y_{1},z_{1}}^{y_{2},z_{2}}\,dF_{x} =-\int\left[F_{x}(x,y_{2},z_{2})-F_{x}(x,y_{1},z_{1}) \right]\,dx
\end{equation*}
At point \(P_{1}\text{,}\) \(\,dx\) is +ve (front part) and at \(P_{2}\text{,}\) \(\,dx\) is -ve (back part).
\begin{equation*}
\therefore \iint\limits_{S} \left[\vec{\nabla} \times \hat{i}F_{x}\right]\cdot\hat{n}\,dS = \int F_{x}(x,y_{2},z_{2})\,dx+F_{x}(x,y_{1},z_{1})\,dx
\end{equation*}
\begin{equation*}
= \int\limits_{C} F_{x}\,dx
\end{equation*}
Similarly, we can find,
\begin{equation*}
\iint\limits_{S} \left[\vec{\nabla} \times \hat{j}F_{y}\right]\cdot\hat{n}\,dS = \int\limits_{C} F_{y}\,dy
\end{equation*}
and
\begin{equation*}
\iint\limits_{S} \left[\vec{\nabla} \times \hat{k}F_{z}\right]\cdot\hat{n}\,dS = \int\limits_{C} F_{z}\,dz
\end{equation*}
Combining these we get,
\begin{equation*}
\iint\limits_{S} \left[\vec{\nabla} \times \vec{F}\right]\cdot\hat{n}\,dS = \oint_{C} \vec{F}\cdot \vec{\,dr}
\end{equation*}