Subsection 1.6.5 Cylindrical Orthogonal Curvilinear Coordinates
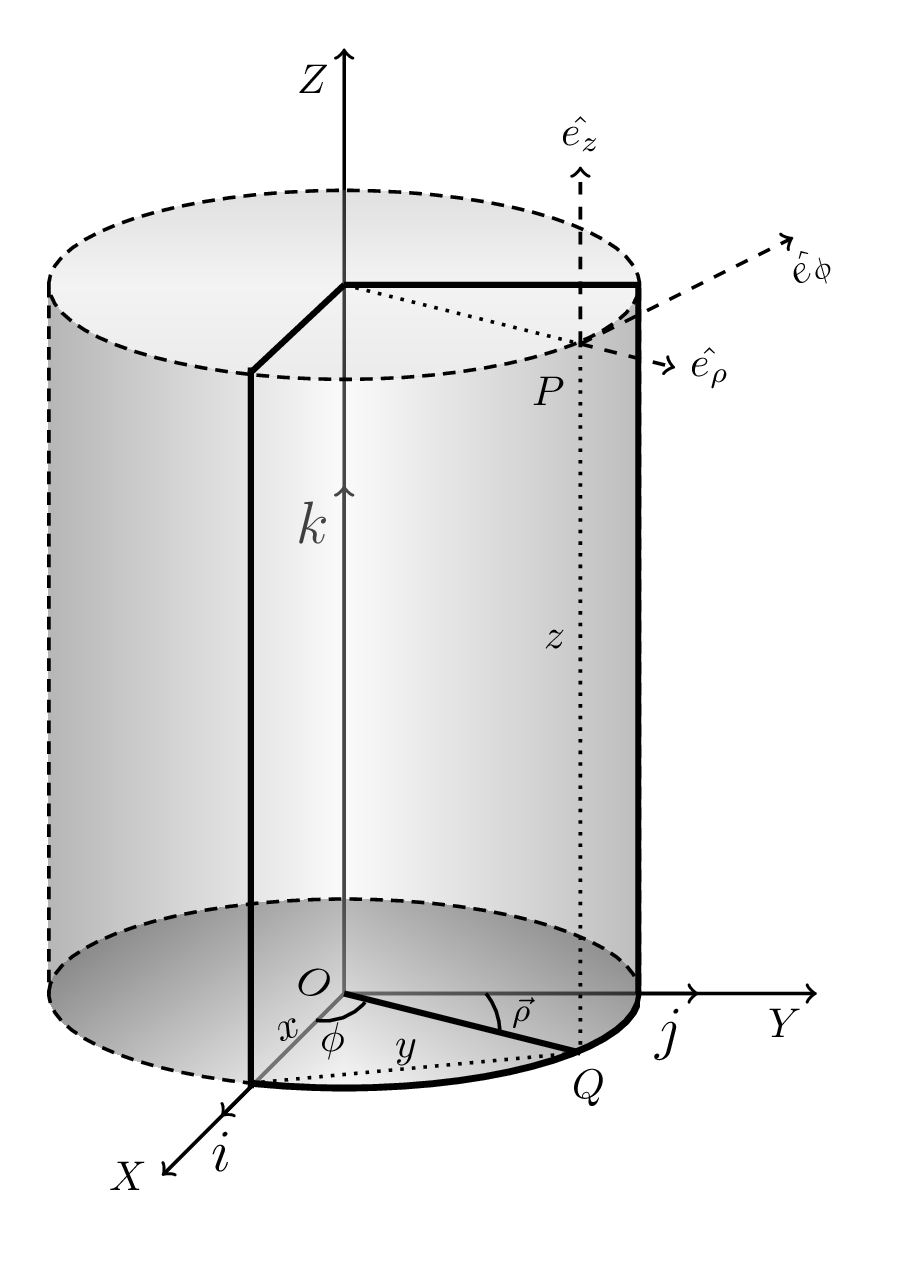
Let the curvilinear coordinates of point P in space be \((u,v,w)\) and corresponding cartesian coordinates be \((x,y,z)\text{.}\) The projection of point P on the z-plane is Q as shown in Figure 1.6.2, whose polar coordinates in this plane are \((\rho, \phi)\text{.}\) The cylindrical coordinates of point P are then specified by \((\rho, \phi, z)\) where, \((\rho\geq 0, \quad 0\leq\phi\leq 2\pi,\quad -\infty \lt z \lt \infty)\text{.}\) The corresponding transformation into cartesian systems are
\begin{equation}
x=\rho \cos\phi, \quad y= \rho\sin\phi, \quad z=z\tag{1.6.11}
\end{equation}
Let \(\vec{r}= x\hat{i}+y\hat{j}+z\hat{k}\) be the position vector of point P in a cartesian system, then we can write
\begin{equation}
\vec{r}= \rho \cos\phi\hat{i}+\rho \sin\phi\hat{j}+z\hat{k} \tag{1.6.12}
\end{equation}
[from eqn. (1.6.11)], in a cylindrical system. Now the tangent vectors of \(\vec{r}\) in a cylindrical system are
\begin{equation*}
\frac{\partial\vec{r}}{\partial \rho} = \cos\phi\hat{i}+\sin\phi\hat{j}+0.\hat{k},
\end{equation*}
\begin{equation*}
\frac{\partial\vec{r}}{\partial \phi} = -\rho\sin\phi\hat{i}+\rho\cos\phi\hat{j}+0.\hat{k},
\end{equation*}
\begin{equation*}
\text{and} \quad \frac{\partial\vec{r}}{\partial z} = \hat{k}.
\end{equation*}
But, scale factors are the magnitude of tangent vectors, then we have -
\begin{equation*}
h_{1}=\mid\frac{\partial\vec{r}}{\partial \rho}\mid = \sqrt{\cos^{2}\phi + \sin^{2}\phi}=1;
\end{equation*}
\begin{equation*}
h_{2}=\mid\frac{\partial\vec{r}}{\partial \phi}\mid = \rho ;
\end{equation*}
\begin{equation*}
\text{and} \quad h_{3}=\mid\frac{\partial\vec{r}}{\partial z}\mid = 1.
\end{equation*}
If \(\hat{e}_{\rho}, \hat{e}_{\phi}, \hat{e}_{z}\) are the unit tangent vectors along the curves \(u,v,w\text{,}\) respectively then in cylindrical coordinates, we have -
\begin{equation*}
\,grad\psi = \vec{\nabla\psi}= \frac{\hat{e}_{\rho}}{1}\frac{\partial\psi}{\partial \rho}
+\frac{\hat{e}_{\phi}}{\rho}\frac{\partial\psi}{\partial \phi}+\frac{\hat{e}_{z}}{1}\frac{\partial\psi}{\partial z},
\end{equation*}
\begin{equation*}
\left[\because \vec{\nabla} = \frac{\hat{e_{1}}}{h_{1}}\frac{\partial}{\partial u}
+\frac{\hat{e_{2}}}{h_{2}}\frac{\partial}{\partial v}
+\frac{\hat{e_{3}}}{h_{3}}\frac{\partial}{\partial w}\right]
\end{equation*}
in curvilinear coordinates.
\begin{equation*}
\,div\vec{F} = \vec{\nabla}\cdot\vec{F}
= \frac{1}{\rho}\left[\frac{\partial}{\partial \rho}(F_{1}\rho)
+\frac{\partial}{\partial \phi}(F_{2})
+\frac{\partial}{\partial z}(F_{3}\rho)\right],
\end{equation*}
\begin{equation*}
curl\vec{F} = \vec{\nabla}\times\vec{F}= {\begin{vmatrix}
\hat{e}_{\rho} & \rho\hat{e}_{\phi} & \hat{e}_{z} \\
\frac{\partial}{\partial \rho} & \frac{\partial}{\partial \phi} & \frac{\partial}{\partial z} \\
F_{1} & \rho F_{2} & F_{3}
\end{vmatrix}}
\end{equation*}
and
\begin{equation*}
\nabla^{2}\psi
= \frac{1}{\rho}\left[\frac{\partial}{\partial \rho}\left(\rho\frac{\partial \psi}{\partial \rho}\right)
+\frac{\partial}{\partial \phi}\left(\frac{1}{\rho}\frac{\partial \psi}{\partial \phi}\right))
+\frac{\partial}{\partial z}\left(\rho\frac{\partial \psi}{\partial z}\right)\right]
\end{equation*}
\begin{equation*}
=\frac{1}{\rho}\frac{\partial\psi}{\partial \rho}
+ \frac{\partial^{2}\psi}{\partial \rho^{2}}
+ \frac{1}{\rho^{2}}\frac{\partial^{2}\psi}{\partial \phi^{2}}
+\frac{1}{\rho}\frac{\partial^{2}\psi}{\partial z^{2}}.
\end{equation*}
we can also find the values of \(h_{1},h_{2},h_{3}\) as -
\begin{equation*}
x=\rho \cos\phi, \quad y= \rho\sin\phi, \quad z=z,
\end{equation*}
and
\begin{equation*}
\rho^{2} = x^{2} + y^{2}, \quad \phi= \tan^{-1}\frac{y}{x}, \quad z=z.
\end{equation*}
Now, if \(x\) is a function of \(\rho, \phi, z\text{,}\) i.e. \(x=x(\rho, \phi,z)\text{,}\) then
\begin{equation*}
\,dx= \frac{\partial x}{\partial \rho}\,d\rho + \frac{\partial x}{\partial \phi}\,d\phi
+ \frac{\partial x}{\partial z}\,dz=\cos\phi \,d\rho-\rho \sin\phi d\phi+0.
\end{equation*}
\begin{equation*}
\text{similarly,} \,dy= \sin\phi \,d\rho+\rho \cos\phi \,d\phi+0,
\end{equation*}
and
\begin{equation*}
\,dz=\,dz.
\end{equation*}
\begin{equation*}
\therefore \,ds^{2}= \vec{dr}\cdot\vec{dr} = \,dx^{2}+\,dy^{2}+\,dz^{2}
\end{equation*}
\begin{equation}
= \,d\rho^{2}+\rho^{2}\,d\phi^{2}+\,dz^{2}\tag{1.6.13}
\end{equation}
But in curvilinear coordinates,
\begin{equation}
\,ds^{2}= h_{1}^{2} \,du^{2}+h_{2}^{2} \,dv^{2}+h_{3}^{2} \,dw^{2}\tag{1.6.14}
\end{equation}
\(h_{1} = 1,\quad h_{2}=\rho, \quad h_{3}=1;\) and \(\hat{e}_{1} =\hat{e}_{\rho},\quad
\hat{e}_{2} =\hat{e}_{\phi}, \quad \hat{e}_{3} =\hat{e}_{z}\text{.}\)
