Subsection 1.4.1 The Line Integral
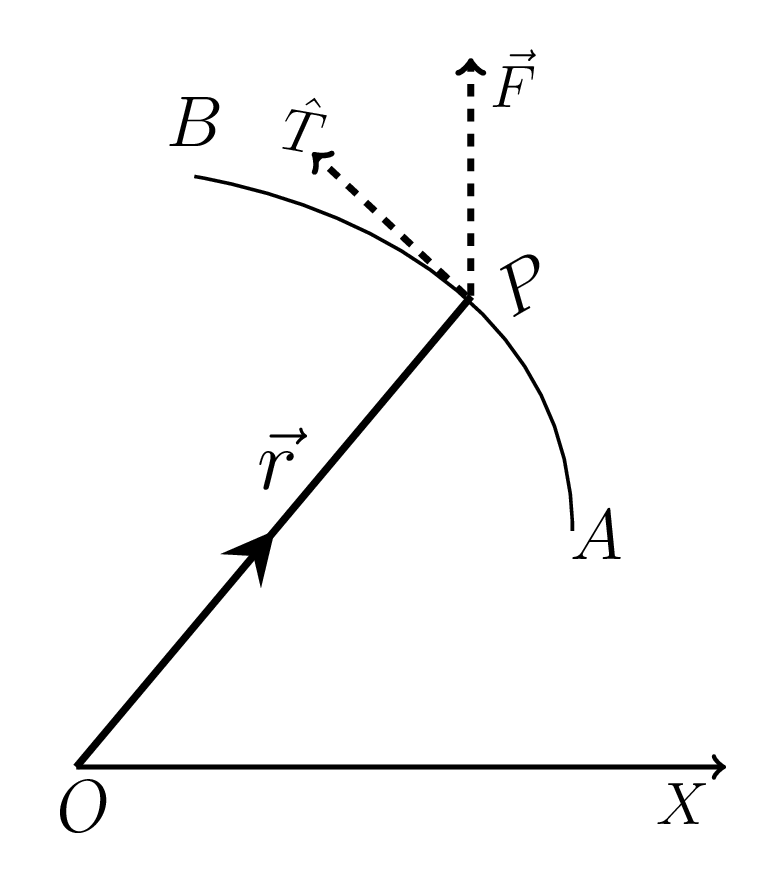
Let us consider a curve \(AB\text{,}\) as shown in Figure 1.4.1 and a vector function \(\vec{F}(x,y,z)\) acting at a point P then the line integral of a vector function \(\vec{F}\) along that curve is defined as integral of the component of \(\vec{F}\) along the tangent to the curve \(AB\text{.}\) Therefore, the component of \(\vec{F}\) along a tangent \(PT\) at P = dot product of \(\vec{F}\) with a unit vector along \(PT\text{.}\)
\begin{equation*}
\text{or,}\quad \vec{F}\cdot \hat{T}=\vec{F}\cdot \frac{\,d\vec{r}}{\,ds}
\end{equation*}
[\(\because \frac{\,d\vec{r}}{\,ds}\) is a unit vector along \(PT\) and \(\,d\vec{r}\) is a small element and \(\,ds\) is a small arc of curve at P.]
\begin{equation*}
\therefore \text{Line integral}\quad = \sum\vec{F}\cdot \frac{\,d\vec{r}}{\,ds},
\end{equation*}
from A to B along the curve
\begin{equation*}
=\int_{c}\left(\vec{F}\cdot \frac{\,d\vec{r}}{\,ds}\right) \,ds = \int_{c}\vec{F}\cdot \,d\vec{r}.
\end{equation*}
If a force \(\vec{F}\) is acting on a particle along arc AB, then the line integral gives the total work done by the force as work done = \(\int^{B}_{A} \vec{F}\cdot \,d\vec{r}\text{.}\) If \(\vec{F}\) be the velocity of a liquid, then the line integral \(\int_{c}\vec{F}\cdot \,d\vec{r}\) is called the flow of a vector field along the curve \(\mathcal{C}\) or the circulation of \(\vec{F}\) around the curve \(\mathcal{C}\text{.}\) If \(\int_{c}\vec{F}\cdot \,d\vec{r} = 0\text{,}\) then, \(\vec{F}\) is called an irrotational vector. The integration around a closed curve is denoted by the symbol \(\oint\) in place of \(\int\text{.}\)
