Subsection 1.1.5 Product of Two Vectors
There are two ways in which vectors are multiplied. The product of one of them is a scalar quantity, called a scalar product (or a dot product) and the other is a vector quantity, called a vector product (or a cross product).
Subsubsection 1.1.5.1 Scalar or Dot Product
- The scalar or dot product of two vectors \(\vec{a}\text{,}\) and \(\vec{b}\) is denoted by \(\vec{a}. \vec{b}\) and is defined as\begin{equation*} \vec{a}\cdot {\vec{b}} = |\vec{a}|. |\vec{b}| \cos\theta= ab\cos\theta\text{,} \end{equation*}where \(\theta\) is the angle between \(\vec{a}\) and \(\vec{b}\text{.}\)
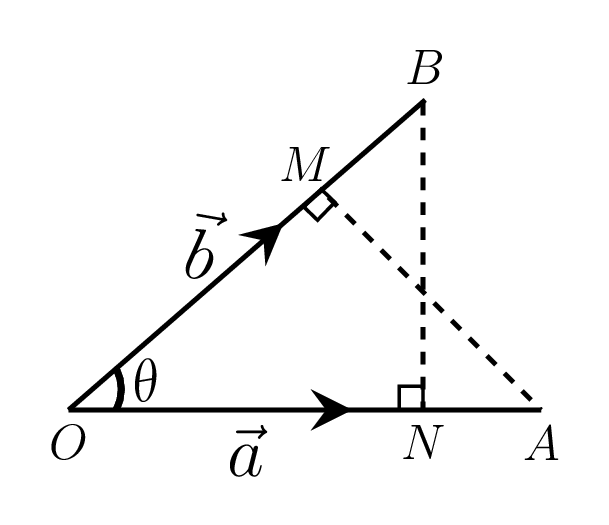
- Geometrical Interpretation: Let \(\vec{OA} =\vec{a}\) and \(\vec{OB} =\vec{b}\text{,}\) as shown in Figure 1.1.7.(a), then\begin{equation*} \vec{a}\cdot {\vec{b}} = \vec{OA}\cdot {\vec{OB}} = OA.OB \cos\theta = OA\cdot {ON} \end{equation*}\([\because \cos\theta= \frac{ON}{OB}]\) = (length of \(\vec{a}\)) (projection of \(\vec{b}\) along a \(\vec{a}\)). The dot product of two vectors is the product of length of one of these vectors and the projection of another in the direction of the first.
Properties:.
- Commutative Law:\begin{align*} \vec{a}\cdot {\vec{b}} \amp = \vec{b}\cdot {\vec{a}}\\ \because [\vec{a}\cdot {\vec{b}}\amp = ab\cos\theta] \quad \text{and} [\vec{b}\cdot {\vec{a}} = ba\cos(-\theta) = ab\cos\theta ] \\ \amp [\because \cos(-\theta) = \cos\theta ]\\ \therefore \quad \vec{a}\cdot {\vec{b}}\amp =\vec{b}\cdot {\vec{a}} \end{align*}
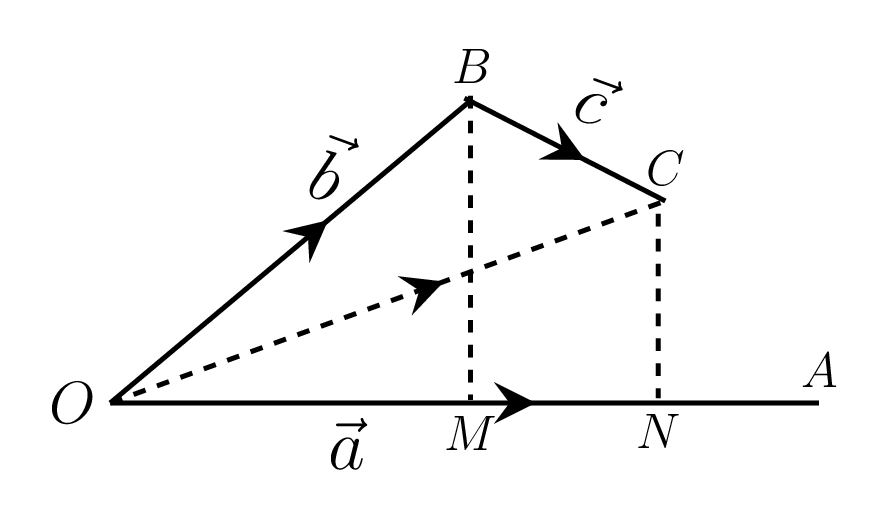
- Distributive Law:\begin{equation*} \vec{a}\cdot{(\vec{b}+\vec{c})}= \vec{a}\cdot {\vec{b}} + \vec{a}\cdot {\vec{c}} \end{equation*}Let \(\vec{OA} =\vec{a}\text{,}\) \(\vec{OB} =\vec{b}\text{,}\) and \(\vec{BC} =\vec{c}\) as shown in Figure 1.1.7.(b), then\begin{equation*} \vec{a}\cdot {\vec{b}} + \vec{a}\cdot {\vec{c}} = \vec{OA}\cdot {\vec{OB}} + \vec{OA}\cdot {\vec{BC}} \end{equation*}\begin{equation*} = OA\cdot{OM}+OA\cdot{MN} = OA(OM+MN) = OA.ON \end{equation*}\begin{equation*} \vec{a}\cdot{(\vec{b}+\vec{c})} = \vec{OA}\cdot{(\vec{OB}+\vec{BC})} = \vec{OA}\cdot{\vec{OC}} = OA.ON \end{equation*}\begin{equation*} \therefore \quad \vec{a}\cdot{(\vec{b}+\vec{c})} = \vec{a}\cdot {\vec{b}} + \vec{a}\cdot {\vec{c}} \end{equation*}
- Useful Results: If \(\hat{i}\text{,}\) \(\hat{j}\text{,}\) \(\hat{k}\text{,}\) be the unit vector along \(x\text{,}\) \(y\text{,}\) \(z\) axes, respectively, then\begin{align*} \hat{i}\cdot{\hat{i}} \amp = \hat{j}\cdot{\hat{j}} = \hat{k}\cdot{\hat{k}} =1 \hspace{1cm} \because \theta = 0^{o}\\ \hat{i}\cdot{\hat{j}} \amp = \hat{j}\cdot{\hat{k}} = \hat{k}\cdot{\hat{i}} = 0 \hspace{1cm} \because \theta = 90^{o} \end{align*}
Subsubsection 1.1.5.2 Vector or Cross Product
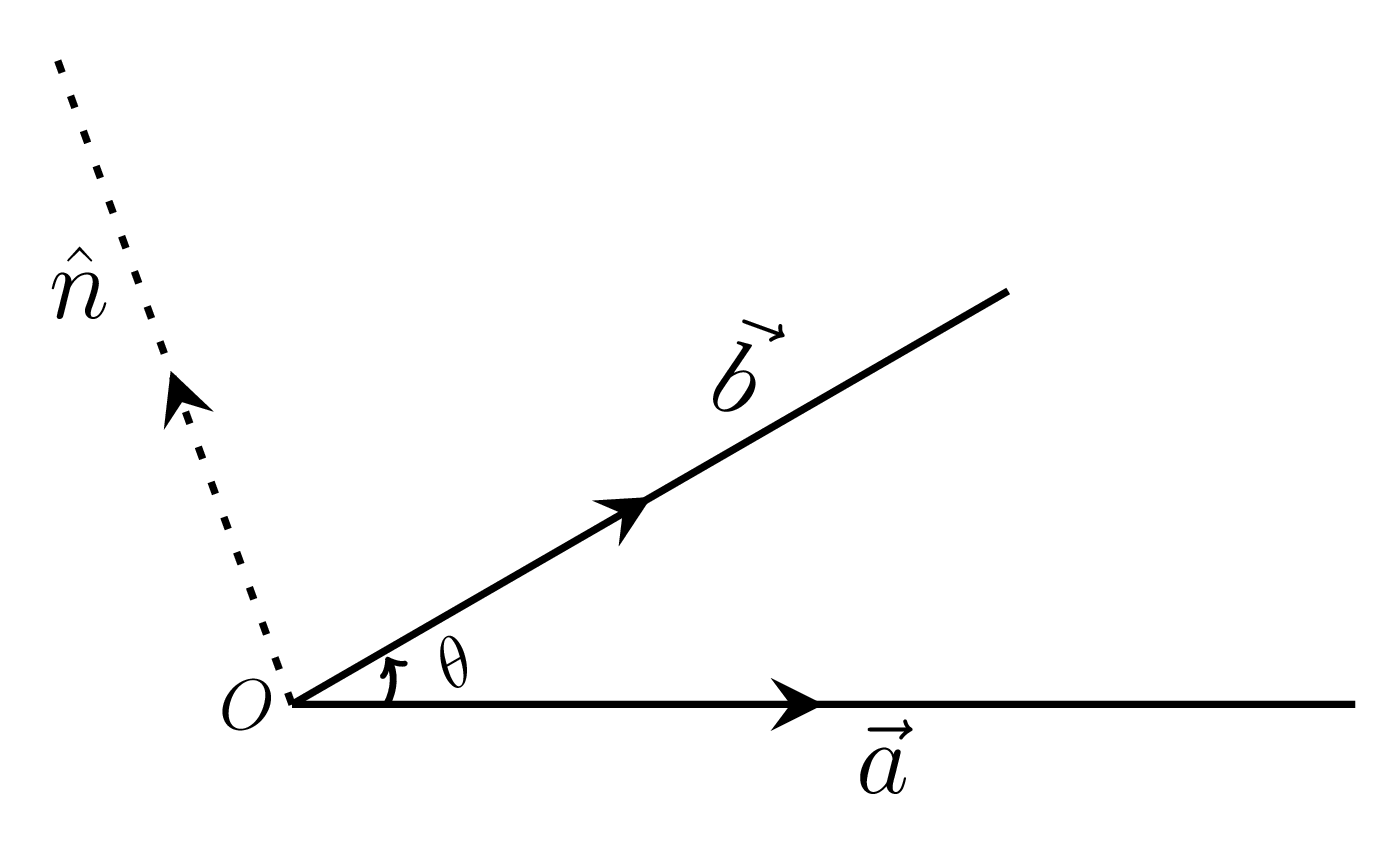
- The vector or cross product of two vectors \(\vec{a}\) and \(\vec{b}\) is denoted by \(\vec{a} \times\vec{b}\) and is defined as\begin{align*} \vec{a} \times \vec{b} \amp = \mid{\vec{a}}\mid \mid{\vec{b}}\mid \sin\theta \cdot{\hat {n}} = ab\sin\theta {\hat{n}} \end{align*}where \(\theta\) is the anlge between \(\vec{a}\) and \(\vec{b}\text{,}\) and \({\hat{n}}\) is an unit vector perpendicular to the plane made by vectors \(\vec{a}\) and \(\vec{b}\) and is representing the direction of \(\vec{a}\times\vec{b}\text{.}\) Here \(\vec{a}\text{,}\) \(\vec{b}\text{,}\) and \({\hat{n}}\) form a right handed system, as shown in Figure 1.1.8.(a).
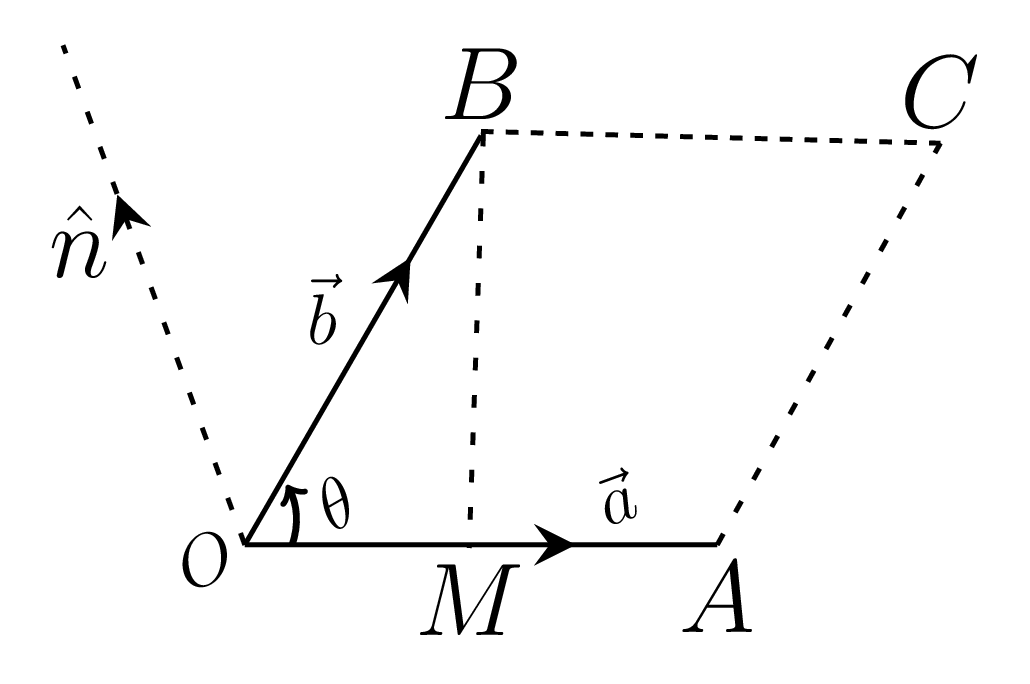
- Geometrical Interpretation: Let \(\vec{a}\) and \(\vec{b}\) be the adjacent sides of the parallelogram, as shown in Figure 1.1.8.(b), then\begin{equation*} \vec{a}\times\vec{b} =\vec{OA}\times\vec{OB} = OA\cdot{OB \sin\theta}{\hat{n}} \end{equation*}\begin{equation*} = OA\cdot{BM}{\hat{n}} = base \cdot height\hspace{3pt} \hat{n} = \text{vector area of parallelogram OACB} \end{equation*}
Hence, a vector product of two vectors is the vector area of a parallelogram constructed by the given vectors.
Properties:.
- Commutative law does not hold good in a vector product, i.e.,\begin{align*} \vec{a}\times\vec{b} \amp \neq \vec{b}\times\vec{a}\\ \text{but,} \quad \vec{a}\times\vec{b} \amp = - \vec{b}\times\vec{a}\\ \because \vec{b}\times\vec{a} \amp = \mid{\vec{b}}\mid \mid{\vec{a}}\mid \sin\theta \cdot \hat {n} = -a b \sin\theta = - \vec{a}\times\vec{b} \end{align*}
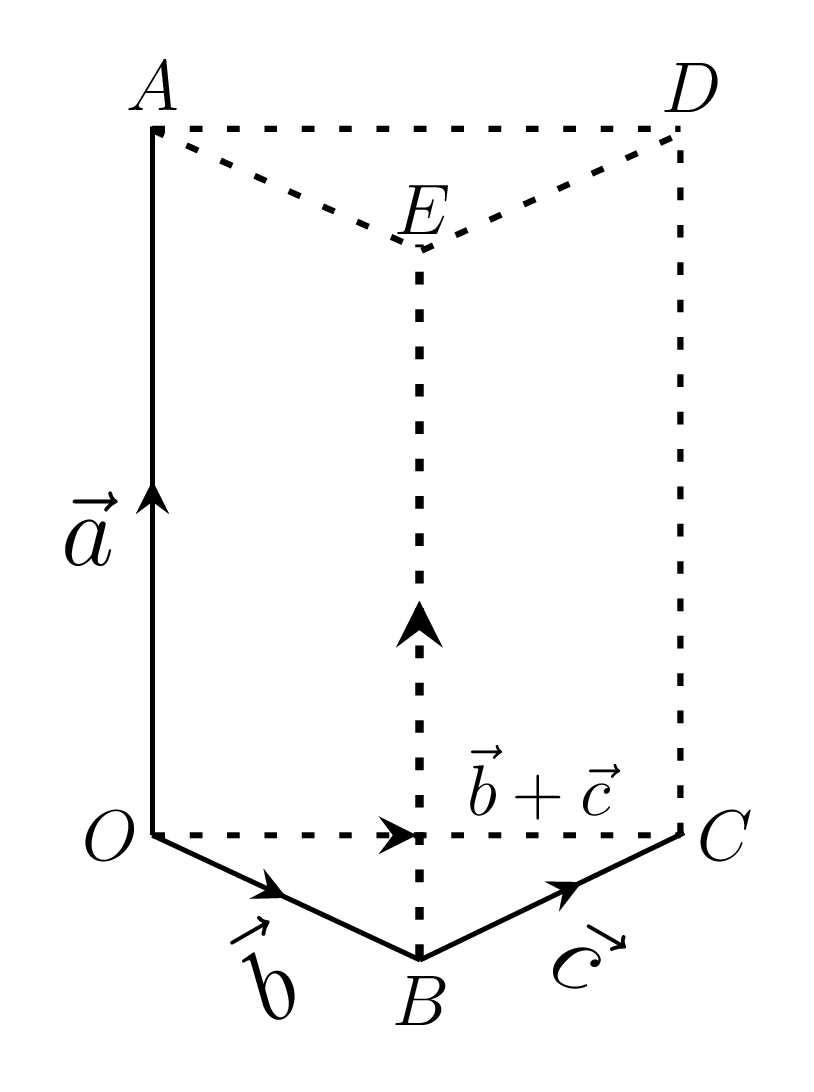
- Distributive law:\begin{equation*} \vec{a}\times{(\vec{b} + \vec{c})} = \vec{a}\times\vec{b} + \vec{a}\times\vec{c} \end{equation*}Let \(\vec{a}\text{,}\) \(\vec{b}\text{,}\) and \(\vec{c}\) are three vectors such that \(\vec{OA}= \vec{a}\text{,}\) \(\vec{OB}= \vec{b}\text{,}\) and \(\vec{BC}= \vec{c}\) that form a parallelogram OAEB, BCDE, and OADC, as shown in Figure 1.1.9.(a), then\begin{equation*} \vec{a}\times\vec{b} + \vec{a}\times\vec{c} \end{equation*}= vector area of \(\Vert^{gm} OAEB\) + vector area of \(\Vert^{gm} BCDE\) = vector area of OAEDCBO = vector area of OADCO - vector area of \(\nabla OBC\) + vector area of \(\nabla AED\)\begin{equation*} [\because \nabla OBC = \nabla AED] \end{equation*}= vector area of \(\Vert^{gm}OADCO = \vec{OA}\times\vec{OC} = \vec{a}\times (\vec{b} + \vec{c})\text{.}\)\begin{equation*} \therefore \quad \vec{a}\times (\vec{b} + \vec{c}) = \vec{a}\times\vec{b} + \vec{a}\times\vec{c} \end{equation*}
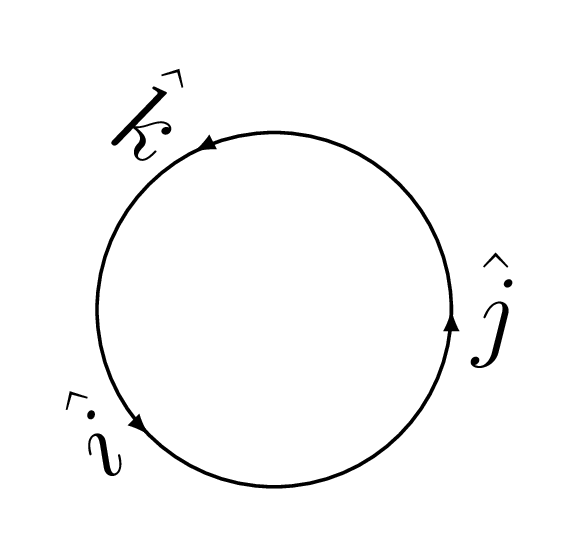
- Useful Results: If \(\hat{i}\text{,}\) \(\hat{j}\text{,}\) and \(\hat{k}\) are mutually perpendicular unit vectors, then from Figure 1.1.9.(b)\begin{align*} \hat{i}\times\hat{i}\amp = \hat{j}\times\hat{j} = \hat{k}\times\hat{k} = 0. \quad [\because \theta = 0] \\ \text{also,} \quad \hat{i}\times\hat{j}\amp = \hat{k}; \quad \hat{j}\times\hat{i} = -\hat{k}; \quad \hat{j}\times\hat{k} = \hat{i}\\ \text{and} \quad \hat{k}\times\hat{j} \amp = -\hat{i}; \quad \hat{k}\times\hat{i} = \hat{j} = - \hat{i}\times\hat{k} \end{align*}
- Vector product can also be expressed as a determinant form. If \(\vec{a} = a_{1}\hat{i}+a_{2}\hat{j}+ a_{3}\hat{k}\) and \(\vec{b} = b_{1}\hat{i}+b_{2}\hat{j}+ b_{3}\hat{k}\text{,}\) then\begin{align*} \vec{a}\times\vec{b} \amp = {a_{1}\hat{i}+a_{2}\hat{j}+ a_{3}\hat{k}}\times{b_{1}\hat{i}+b_{2}\hat{j} + b_{3}\hat{k}}\\ \amp =(a_{2}b_{3}-(a_{3}b_{2})\hat{i}- (a_{1}b_{3}-(a_{3}b_{1})\hat{j} + (a_{1}b_{2}-(a_{2}b_{1})\hat{k} \end{align*}\(=\begin{Vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{Vmatrix}\)