Example 5.2.1.
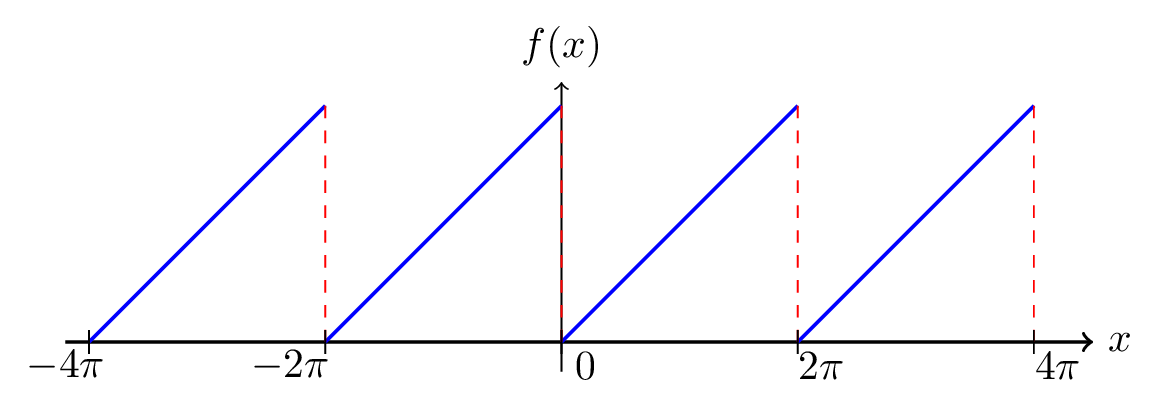
Find the Fourier series expansion of \(f(x) =x\text{,}\) where \(0\lt x \lt 2\pi\text{,}\) and sketch its graph from \(x=-4\pi\) to \(4\pi\text{.}\)
Solution.
Let
\begin{equation*}
f(x) = x = \frac{a_{o}}{2} + \sum\limits_{n=1}^{\infty}\left[a_{n}\cos nx + b_{n}\sin nx\right]
\end{equation*}
where
\begin{equation*}
a_{o} = \frac{1}{\pi}\int\limits_{0}^{2\pi}f(x)\,dx = \frac{1}{\pi}\int\limits_{0}^{2\pi}x\,dx = \frac{1}{\pi}\left[\frac{x^{2}}{2}\right]^{2\pi}_{0} = 2\pi.
\end{equation*}
\begin{equation*}
a_{n}= \frac{1}{\pi}\int\limits_{0}^{2\pi} f(x)\cos nx \,dx = \frac{1}{\pi}\int\limits_{0}^{2\pi} x\cos nx \,dx
\end{equation*}
\begin{equation*}
= \frac{1}{\pi}\left[x.\frac{\sin nx}{n}-1.\frac{\cos nx}{-n^{2}}\right]_{0}^{2\pi}
\end{equation*}
\begin{equation*}
=\frac{1}{\pi}\left[0+\frac{1}{n^{2}}(\cos 2n\pi-\cos 0)\right]= \frac{1}{\pi}\left[\frac{1}{n^{2}}(1-1)\right] = 0.
\end{equation*}
and
\begin{equation*}
b_{n}= \frac{1}{\pi}\int\limits_{0}^{2\pi} f(x)\sin nx \,dx = \frac{1}{\pi}\int\limits_{0}^{2\pi} x\sin nx \,dx
\end{equation*}
\begin{equation*}
= \frac{1}{\pi}\left[x.\frac{\cos nx}{-n}-1.\frac{\sin nx}{-n^{2}}\right]_{0}^{2\pi}
\end{equation*}
\begin{equation*}
=\frac{1}{\pi}\left[\frac{2\pi \cos 2n \pi}{-n}+\frac{1}{n^{2}}\left(\sin nx\right)_{0}^{2\pi}\right]= -\frac{2}{n}.
\end{equation*}
Substituting these values in expression \(f(x)\text{,}\) we get -
\begin{equation*}
x=\pi - 2\left[\sin x+\frac{\sin 2x}{2}+\frac{\sin 3x}{3}+\cdots\right]
\end{equation*}
The graphical representation of the given function is shown in figure below.